>	restart:#"m05_p41"

Por un conducto circula vapor de agua a 150 kPa y 200 C, con una presin dinámica de 50 kPa. Se pide:
a) Determinar el estado termodinámico y la densidad.
b) Determinar expresiones explcitas para la velocidad de la corriente con el modelo de fluido incompresible y con el modelo de gas perfecto.
c) Calcular la velocidad de la corriente con ambos modelos.
d) Calcular la velocidad del sonido en el vapor en esas condiciones.
e) Indicar cmo se podra medir la presin dinámica de la corriente.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="H2O":dat:=[p1=150e3*Pa_,T1=(200+273)*K_,p[d]=50e3*Pa_];

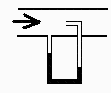
Esquema:

>

>

Eqs. const.:

>	eq1_MLP:=eq5_55;eq2_MLP:=T[t]=T;eq1_MGP:=subs(T[2]=T[t],T[1]=T,p[2]=p[t],p[1]=p,eq1_22);eq2_MGP:=T[t]=T+v^2/(2*c[p]);gdat:=get_gas_data(su1):dat:=op(dat),gdat,Const,SI2,SI1:get_pv_data(su1):

a) Determinar el estado termodinámico y la densidad.

>	pv1:='pv(T1)';pv1_:=subs(dat,evalf(subs(dat,pv(T1)))):'pv1'=evalf(%,2);eqrho:=rho=p1/(R*T1);eqrho_:=subs(dat,eqrho);

Como pv1>p1, se trata de vapor sobrecalentado (vapor seco).

b) Determinar expresiones explcitas para la velocidad de la corriente con el modelo de fluido incompresible y con el modelo de gas perfecto.

La presin dinámica es la diferencia entre la presin total (o de remanso) y la estática.

>	eqpd:=p[t]=p+p[d];eqMLP:=v=solve(subs(eqpd,z=0,eq1_MLP),v)[1];eqMGP:=v=solve(subs(eqpd,eq2_MGP),v)[1];eqMGP_:=simplify(subs(T[t]=T*(p[t]/p)^((gamma-1)/gamma),eqMGP));eqMGP__:=(subs(T=p/(rho*R),eqMGP_));

Es fácil comprobar que el primer trmino del desarrollo de esta ltima expresin coincide con el del modelo incompresible.

c) Calcular la velocidad de la corriente con ambos modelos.

>	eqMLP_:=simplify(evalf(subs(eqrho,dat,eqMLP))):eqMLP:=v=evalf(subs(SI0,rhs(%))*m_/s_);eqMGP___:=evalf(subs(eqpd,dat,eqrho,p=p1,T=T1,dat,eqMGP__));

d) Calcular la velocidad del sonido en el vapor.

>	eqc:=c=sqrt(gamma*R*T);eqc_:=evalf(subs(T=T1,dat,eqc));eqMach:=M=v/c;evalf(subs(eqc_,eqMGP___,eqMach));

e) Indicar cmo se podra medir la presin dinámica de la corriente.

Con un pitot, como se indica arriba.

>