>	restart:#"m05_p39"

Un cilindro vertical de 5 cm de diámetro contiene aire limitado por arriba por un émbolo de 10 kg (supóngase sin fugas ni fricción), y por abajo por una base con un orificio que puede comunicar con un depósito de aire comprimido a 0,8 MPa, estando el ambiente a 20 ºC y 93 kPa. Inicialmente el émbolo está a 20 cm de la base. En un cierto instante, se ponen en comunicación cilindro y depósito durante 1 s, observándose que al cabo de mucho tiempo el émbolo ha quedado a 35 cm de la base. Se pide:
a) Hacer un esquema de los estados inicial y final: Calcular la masa de aire inicial y la que ha entrado. Determinar la evolución del gas si en el proceso pudiese considerarse que el émbolo apenas se acelera, calculando el intercambio térmico con el exterior.
b) Un modelo para el estudio del movimiento sería suponer que el aire entra tan deprisa que el émbolo no se ha movido apreciablemente durante la entrada. Calcular las condiciones termodinámicas inmediatamente después de la entrada de toda la masa.
c) Calcular la altura máxima a la que podría subir el émbolo.
d) Estimar el periodo del émbolo para discernir si durante el llenado se ha movido apreciablemente.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):assume(sol1>0);

>	su:="Aire":dat:=[D=0.05*m_,mE=10*kg_,pdep=0.8e6*Pa_,T0=(20+273)*K_,p0=93e3*Pa_,z1=0.20*m_,z2=0.35*m_]:dat:=[op(dat),A=evalf(subs(dat,(Pi*D^2/4)))];

Esquema:

>

>

Eqs. const.:

>	eqET:=subs(eq1_11,eq1_12);eqEE:=eq1_16;gdat:=get_gas_data(su):dat:=op(dat),gdat,Const,SI2,SI1:

a)  Hacer un esquema de los estados inicial y final: Calcular la masa de aire inicial y la que ha entrado. Determinar la evolución del gas si en el proceso pudiese considerarse que el émbolo apenas se acelera, calculando el intercambio térmico con el exterior.

>

T1:=T0;p1:=p0+mE*g/A;p1_:=subs(dat,SI1,p1):'p1'=evalf(%/(1000*Pa_/kPa_));m1:='p1*A*z1/(R*T1)';m1_:=subs(dat,m1);T2:=T0;p2:=p0+mE*g/A;p2_:=subs(dat,SI1,p2):'p2'=evalf(%/(1000*Pa_/kPa_));m2:='p2*A*z2/(R*T2)';m2_:=subs(dat,m2);Dm12=evalf(m2_-m1_);eqBE:='D(m*c[v]*T)=Q+W+c[p]*T0*Dm';eqBE:='c[v]*T0*Dm=Q-p2*A*Dz+(c[v]+R)*T0*Dm';eqBE:='0=Q-p2*A*Dz+R*T0*Dm';eqBE:=0=Q;

b) Un modelo para el estudio del movimiento sería suponer que el aire entra tan deprisa que el émbolo no se ha movido apreciablemente durante la entrada. Calcular las condiciones termodinámicas inmediatamente después de la entrada de toda la masa.

>	V11:=A*z1;eqBM:=m11='m2';assign(%):eqBE:='m11*u11-m1*u1=Q+W+h[dep]*(m11-m1)';eqBE:='m11*c[v]*T11-m1*c[v]*T1=c[p]*T0*(m11-m1)';T11_:=subs(dat,solve(eqBE,T11));p11:='m11*R*T11/V11';p11_:=subs(T11=T11_,dat,p11);

c) Calcular la altura máxima a la que podría subir el émbolo.

>

eq1:='m11*c[v]*(T12-T11)+mE*g*(z12-z1)=-p0*A*(z12-z1)';eq1_:=subs(m11=m11_,T11=T11_,dat,SI0,eq1);eq2:=subs(m=m11,p=p12,V=A*z12,T=T12,eqET);eq2_:=subs(m11=m11_,p=p12,V=A*z12,T=T12,dat,SI0,eq2);eq3:='p12*z12^gamma=p11*z1^gamma';eq3_:=subs(T11=T11_,dat,SI0,eq3);sol1:=fsolve({eq1_,eq2_,eq3_},{z12,p12,T12},z12=0.3..1);z12_:=subs(sol1,z12)*m_;T12_:=subs(sol1,T12)*K_;p12_:=subs(sol1,p12)*Pa_:'p12'=evalf(p12_/(1e3*Pa_/kPa_));

e) Estimar el periodo del émbolo para discernir si durante el llenado se ha movido apreciablemente.

>	eqBF:=mE*diff(z(t),t,t)=(p-p0)*A-mE*g;eqBF:=mE*diff(z(t),t,t)='(p1*(z1/z(t))^gamma-p1)*A';eqBF:=mE*diff(Dz(t),t,t)='(gamma*Dz(t)/z1)*p1*A';eqBF:=diff(x(t),t,t)=-omega^2*x(t);tau:='2*Pi*sqrt(z1*mE/(gamma*p1*A))';tau_:=evalf(subs(dat,tau));

1 s de tiempo de llenado no es despreciable frente a los 0,8 s de oscilación del émbolo, luego no es adecuado este modelo de dos tiempos característicos y, pese a la aparente rapidez del llenado, no oscilaría mucho el émbolo.

Si pidieran el equilibrio mecánico (estado 13).

>

eq1:=p13=p2;assign(%):eq2:=subs(m=m11,p=p13,V=A*z13,T=T13,eqET);eq2_:=subs(m11=m11_,p=p2_,V=A*z13,T=T13,dat,SI0,eq2);eq3:=p13*z13^gamma=p11*z1^gamma;eq3_:=subs(T11=T11_,dat,SI0,eq3);sol1:=fsolve({eq2_,eq3_},{z13,T13},z13=0.3..0.5);z13_:=Re(subs(sol1,z13))*m_;T13_:=Re(subs(sol1,T13))*K_;p13_:=p2_:'p13'=evalf(p13_/(1e3*Pa_/kPa_));

Simulación del movimiento con algo de fricción.

>

deq1:=diff(z(t),t)=zp(t);deq2:=mE*diff(zp(t),t)=-mE*g+(p-p0)*A-coe*zp(t);ic1:=z(0)='z1';ic2:=zp(0)=0;eqs:=subs(dat,SI0,{deq1,subs(p=p11_*(z1/z(t))^gamma,deq2),ic1,ic2});coe:=25:dsol1:=dsolve(eqs,{z(t),zp(t)},numeric):with(plots):odeplot(dsol1,[t,z(t)],0..1,numpoints=100,labels=["t(seg)","z(m)"],view=[0..1,0..0.5],colour=black);

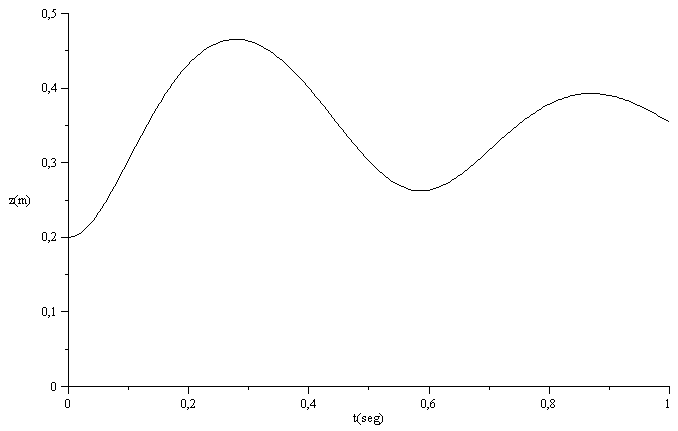La discrepancia entre este periodo de unos 0,55 s y el antes calculado de 0,45 s es debida a la no linealidad del proceso.

>