>	restart:#"m05_p08"

En un conducto divergente de 0,2 m2 de sección de entrada por el que circula aire, se han medido las presiones estáticas y totales de entrada y salida, obteniéndose p1=100 kPa, p1t=120 kPa, p2=105 kPa y p2t=115 kPa. Sabiendo que la temperatura ambiente es de 15 °C, se pide:

a) Gasto de aire, velocidad de entrada y temperatura y velocidad de salida.

b) Rendimiento adiabático de la compresión dinámica.

c) Generación de entropía.

d) Demostrar que para velocidades bajas la presión total y la temperatura total se aproximan a las obtenidas con el modelo de fluido incompresible.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="Aire":dat:=[A1=0.2*m_^2,p1=100e3*Pa_,p1t=120e3*Pa_,p2=105e3*Pa_,p2t=115e3*Pa_,T1=288*K_];

Esquema:

>

>

Eqs. const.:

>	eqET:=eq1_12;eqEE:=eq1_16;gdat:=get_gas_data(su):dat:=op(dat),Const,gdat,SI2,SI1:

a) Gasto de aire, velocidad de entrada y temperatura y velocidad de salida.

>

eqBM:=eq5_39;eqBE:=eq5_43;eq1:=subs(eqET,p=p1,T=T1,v=v1,A=A1,eqBM);eq2:=subs(eqET,p=p2,T=T2,v=v2,A=A2,eqBM);eq3:=T1t=T1+v1^2/(2*c[p]);eq4:=T2t=T2+v2^2/(2*c[p]);eq5:=T1t/T1=(p1t/p1)^((gamma-1)/gamma);eq6:=T2t/T2=(p2t/p2)^((gamma-1)/gamma);eqBE:=T1t=T2t;sol1:=allvalues(solve(subs(dat,{eq1,eq2,eq3,eq4,eq5,eq6,eqBE}),{m,v1,T1t,T2t,A2,T2,v2}))[1]:'m'=evalf(subs(sol1,m));'v1'=evalf(subs(sol1,v1));'T1t'=evalf(subs(sol1,T1t));'T2t'=evalf(subs(sol1,T2t));'A2'=evalf(subs(sol1,A2));'T2'=evalf(subs(sol1,T2));'v2'=evalf(subs(sol1,v2));#T1t_:=solve(eq3,T1t);T2t_:=T1t_;T2_:=solve(subs(T2t=T2t_,eq6),T2);v1_:=solve(eq3,v1);m_:=solve(subs(v1=v1_,eq1),m);

b) Rendimiento adiabático de la compresión dinámica.

>	eta[tob]:=(1-T2/T1t)/(1-(p2/p1t)^((gamma-1)/gamma));eta[tob_]:=subs(dat,sol1,eta[tob]):'eta[tob]'=evalf(%,2);

c) Generación de entropía.

>	DSdot:=rhs(eq2_16);DSdot_:=evalf(subs(dat,sol1,SI0,DSdot))*W_/K_;

d) Demostrar que para velocidades bajas la presión total y la temperatura total se aproximan a las obtenidas con el modelo de fluido incompresible.

>	Tt:=T+v^2/(2*cp);pt:=p*(Tt/T)^(gamma/(gamma-1));pt_lin:=convert(series(pt,v=0,6),polynom);pt_lin_:=expand(simplify(subs(T=p/(R*rho),gamma=cp/(cp-R),pt_lin)));pt_incompr:=p+rho*v^2/2;

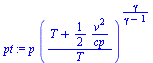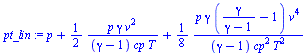Como en este caso la v es alta, la aprox. no es muy buena, pero todavía aceptable.

>	v1_incompr:=sqrt(2*(p1t-p1)/rho);v1_incompr_:=evalf(subs(eqET,p=p1,T=T1,dat,SI0,v1_incompr))*m_/s_;

>