>	restart;#"m04_p34"

Se quiere llenar un depósito de 1 m3 con n-butano líquido, debiendo dejar por seguridad un volumen de gas del 20% a la temperatura máxima de operación, que es de 50ºC. Se pide:
a) Estado termodinámico a 15ºC, si se ha llenado al máximo antedicho (20% libre a 50 ºC).
b) Estimar la densidad en el punto crítico del n-butano con el modelo de estados correspondientes.
c) Determinar la relación de densidades a 15ºC y a 50ºC con el siguiente modelo de estados correspondientes para la densidad reducida de los líquidos en saturación, R=1/Zcr(1TR)2/7.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="C4H10":dat:=[Vt=1*m_^3,Vliq50=0.8*m_^3,T50=(50+273)*K_,T15=(15+273)*K_];eqDat:=rho[R]=1/(Z[cr]^((1-T[R])^(2/7)));

Esquema:

>

>

Eqs. const.:

>	dat:=op(dat),get_gas_data(su),get_liq_data(su),Const,SI2,SI1:get_pv_data(su):

a) Estado termodinámico a 15ºC, si se ha llenado al máximo antedicho (20% libre a 50 ºC).

Con el modelo de líquido perfecto para la fase líquida, seguirá habiendo prácticamente 0,8 m3 de líquido a 15 ºC, ya que el aumento por condensación de 50 ºC a 15 ºC será despreciable.

>

eqMLP:=rho[L]=subs(dat,rho);eqmL:=m[L]=rho[L]*V[L];eqmL_:=subs(dat,m[L]=rho*Vliq50);eqMGP:=rho[V]=p[v]/(R*T);p[v]=p[u]*exp(A-B/((T/T[u]+C)));p50_:=subs(dat,evalf(subs(dat,pv(T50))));p15_:=subs(dat,evalf(subs(dat,pv(T0))));eqmV50:=subs(dat,m[V]=p50_*(Vt-Vliq50)/(R*T50));eqmV15:=subs(dat,m[V]=p15_*(Vt-Vliq50)/(R*T15));eqx:=x=m[V]/(m[V]+m[L]);eqx_:=subs(eqmV15,eqmL_,eqx);

i.e., a 15 ºC hay unos 458 kg de líquido (más casi 2 kg de condensado, pero la incertidumbre en los 458 kg es mayor), más 0,85 kg de vapor (x=0,002), todo ello a 175 kPa. Nótese que, como la masa de vapor es pequeña, no se ha afinado en el modelo (MGP).

Pero el modelo de líquido perfecto puede que no sea bueno para calcular la densidad a 50 ºC (el dato es a 15 ºC). Al final del problema lo revisaremos.

b) Estimar la densidad en el punto crítico con el modelo de estados correspondientes.

Tomaremos el Zcr=0.27 del MEC simple (en realidad para el n-butano es Zcr=0.274).

>	eqPC:=p[cr]*v[cr]=Z[cr]*R*T[cr];eqPC:=rho[cr]=p[cr]/(Z[cr]*R*T[cr]);eqZcr:=Z[cr]=0.27;rhocr_:=subs(eqZcr,dat,p[cr]/(Z[cr]*R*T[cr])):[p[cr],Z[cr],R,T[cr],rho[cr]]=subs(eqZcr,dat,[p[cr],Z[cr],R,T[cr],rhocr_]);

i.e., la densidad en el PC es de 230 kg/m3 (en realidad para el n-butano es rhocr=227,8 kg/m3).

c) Determinar la relación de densidades a 15ºC y a 50ºC con el siguiente modelo de estados correspondientes para la densidad reducida de los líquidos en saturación, R=1/Zcr(1TR)2/7.

>

eqDat_:=eqDat;TR50:=T50/T[cr];TR50_:=subs(dat,%);eqDat_50:=subs(eqZcr,T[R]=TR50_,eqDat);rho50=rho[R]*r[cr];rho50:=subs(eqZcr,eqDat_50,rho[R]*rhocr_);TR15:=T15/T[cr];TR15_:=subs(dat,%);eqDat_15:=subs(eqZcr,T[R]=TR15_,eqDat);rho15=rho[R]*r[cr];rho15:=subs(eqZcr,eqDat_15,rho[R]*rhocr_);eq:='rho15/rho50'=rho15/rho50;

i.e. al enfriarse desde 50 ºC hasta 15 ºC el líquido (supuesto que no interaccionase con el vapor) reduciría su volumen un 7,4%.

>

>

alpha:=(-1/rho)*diff(rho(T),T)[p];alpha:=(-1/rho)*diff(rho(T),T)[sat];alpha:=(-1/(rho[R]*T[cr]))*diff(rho[R](T[R]),T[R])[sat];alpha:=(-1/(rho[R]*T[cr]))*diff(rhs(eqDat),T[R]);TR0:=T0/T[cr];TR0_:=subs(dat,%);eqDat_:=subs(eqZcr,T[R]=TR0_,eqDat);rho0=rho[R]*r[cr];rho0_:=subs(eqZcr,eqDat_,rho[R]*rhocr_);alpha15:=evalf(subs(eqDat,eqZcr,T[R]=TR0,dat,alpha));

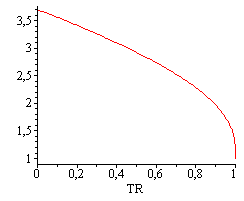
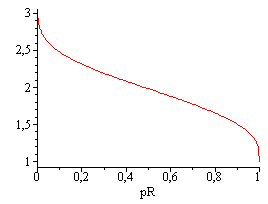
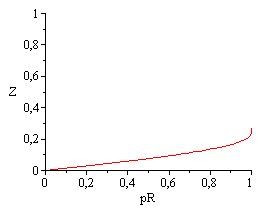
NOTA. Puede representarse rhoR(TR), y rhoR(pR) y Z(pR) si se usa la Ec. de Guggenheim.

>	rhoR:=1/(Z[cr]^((1-TR)^(2/7)));eqG:=ln(pR)=6*(1-1/TR);TR_:=solve(%,TR);rhoR_:=subs(TR=TR_,rhoR);Z=p[R]*Z[cr]/(rho[R]*T[R]);Z_:=subs(TR=TR_,pR*Z[cr]/(rhoR*TR));

>	plot(subs(eqZcr,rhoR),TR=0..1);plot(subs(eqZcr,rhoR_),pR=0..1);plot(subs(eqZcr,[pR,Z_,pR=0..1]),'pR'=0..1,'Z'=0..1);

NOTA. Los valores del NIST son: rhoPC=227,8 kg/m3.

a 15 ºC, pv=175,8 kPa, rhoL=584,2 kg/m3.

a 50 ºC, pv=494,8 kPa, rhoL=542,3 kg/m3.

Densidad en ebull. rhoL=601,5 kg/m3.

>