>	restart:#"m04_p29"

En un recipiente rígido de 10 litros hay amoniaco puro a 100 ºC y 1 MPa. Se pide:
a) Esquematizar el diagrama p-T de las fases del amoniaco, indicando los valores representativos.
b) Determinar la curva de presión de vapor ajustando la expresión pv(T)=Aexp(BT) en el punto de ebullición normal y en el punto crítico (i.e. calcular A y B). ¿Qué relación tiene con la ecuación de Clapeyron?
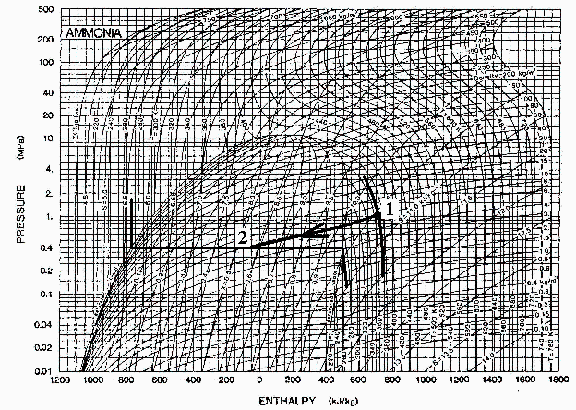
c) Determinar la masa de amoniaco encerrada con ayuda del gráfico del amoniaco, y compararla con la que daría el modelo de gas ideal.
d) Estado final interior cuando el recipiente se introduce en un baño de hielo a 0 ºC.
e) Calor evacuado en el proceso anterior.
f) De las familias de curvas que aparecen en el diagram p-h sólo una de ellas bastaría para obtener las otras; ¿cuál de ellas? ¿Cómo se obtendrían las densidades en función de la familia anterior?
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="NH3":dat:=[V=0.01*m_^3,T1=(100+273)*K_,p1=1e6*Pa_,T2=(0+273)*K_];

Esquema:

>

>

Ecs. const.:

>	dat:=op(dat),get_gas_data(su),get_liq_data(su),Const,SI2,SI1:get_pv_data(su):

a) Esquematizar el diagrama p-T del amoniaco, indicando los valores representativos.

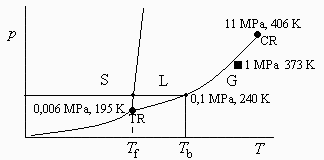
En la Tabla A3.3: Propiedades de gases, viene el punto crítico, y en la Tabla A3.4: Propiedades de líquidos, vienen los puntos de solidificación (Tf) y de ebullición (Tb). La Ttr se aproxima por Tf, y con la ecuación de la presión de vapor (e.g. Antoine) se determina ptr. La misma ecuación permite situar el estado inicial, que resulta gaseoso.

>	T1_:=subs(dat,T1);p1_:=subs(dat,p1);T[cr]=subs(dat,T[cr]);p[cr]=subs(dat,p[cr]);T[f]=subs(dat,T[f]);Ttr:=T[f];p[tr]=p[v](T[tr]);pvTtr:=subs(dat,evalf(subs(dat,pv(T[f])))):p[tr]=evalf(%,2);T[b]=subs(dat,T[b]);

b) Determinar la curva de presión de vapor ajustando la expresión pv(T)=Aexp(BT) en el punto de ebullición normal y en el punto crítico (i.e. calcular A y B). ¿Qué relación tiene con la ecuación de Clapeyron?

>

eqpv:=pv=A*exp(B*T);eqpv_1:=subs(pv=p0,T=T[b],dat,eqpv);eqpv_2:=subs(pv=p[cr],T=T[cr],dat,eqpv);eqpv_:=lhs(eqpv_1)/lhs(eqpv_2)=rhs(eqpv_1)/rhs(eqpv_2):evalf(%,2);B_:=solve(%,B):B=evalf(%,2);A_:=evalf(subs(B=B_,solve(eqpv_1,A))):A=evalf(%,2);eqpv_diff:=dpv/dT=diff(rhs(eqpv),T);eqpv_diff_Clapeyron:=dpv/dT=h[LV]/(T*v[LV]);eqlnpv_Clapeyron_approx:=ln(p[v])=A-h[LV]/(R*T);eqlnpv:=ln(p[v])=diff(rhs(eqpv),T);

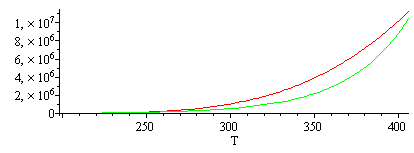
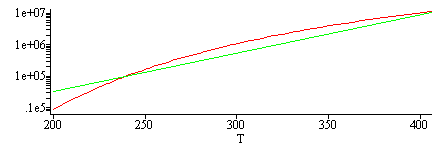
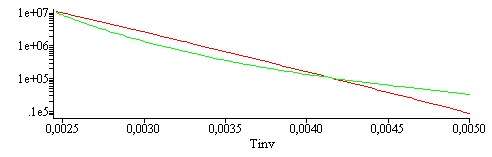
i.e., A=130 Pa y B=0,028 1/K. Esa expresión no es del tipo de la de Clapeyron, que es mucho mejor porque se basa en una relación termodinámica general.

Para visualizar la diferencia se han añadido los gráficos siguientes:

>	plot(subs(SI0,[pv(T),subs(A=A_,B=B_,rhs(eqpv))]),T=200..406);with(plots):logplot(subs(SI0,[pv(T),subs(A=A_,B=B_,rhs(eqpv))]),T=200..406);logplot(subs(T=1/Tinv,SI0,[pv(T),subs(A=A_,B=B_,rhs(eqpv))]),Tinv=1/200..1/406);

Warning, the name changecoords has been redefined

c) Determinar la masa de amoniaco encerrada con ayuda del gráfico del amoniaco, y compararla con la que daría el modelo de gas ideal.

Del gráfico, o, en ausencia de éste, de la presión de vapor a 15 ºC, o de la temperatura de vaporización a 1 MPa, se deduce que está en estado gaseoso.

>	pvT1_:=subs(dat,evalf(subs(dat,pv(T1)))):'pvT1'=evalf(%,2);Tvp1_:=subs(dat,evalf(subs(dat,solve(p1=pv(T),T)))):'Tvp1'=evalf(%,3);

En efecto, a 1 MPa el NH3 hierve a 298 K y está a 373 K, o a 373 K condensaría a 6.3 MPa y está sólo a 1 MPa.

Con el modelo de gas ideal (MGI), la masa sería:

>	eqMGI:=m=p*V/(R*T);eqMGI_:=subs(p=p1,T=T1,dat,eqMGI):evalf(%,2);

Con el modelo de estados correspondientes (MEC), en el gráfico Z-pR se lee Z=0,96 y por tanto:

>	eqMEC:=m=p*V/(Z*R*T);pR1:=p1/p[cr];pR1_:=subs(dat,pR1):'pR1'=evalf(%,2);TR1:=T1/T[cr];TR1_:=subs(dat,TR1):'TR1'=evalf(%,2);Z1_:=0.96;eqMEC_:=subs(Z=Z1_,p=p1,T=T1,dat,eqMEC):evalf(%,2);

Con el diagrama p-h del NH3 se ve que rho=6 kg/m3 y por tanto:

>	rho_dia:=6*kg_/m_^3;m__:=subs(dat,V*rho_dia):'m'=evalf(%,2);

La masa de amoniaco es pues de 0,060 kg (unos 60+/-3 g).

d) Estado final interior cuando el recipiente se introduce en un baño de hielo a 0 ºC.

>	T2=subs(dat,T2);p2_MGI:=m*R*T2/V;p2_MGI_:=subs(eqMGI_,T=T2,dat,p2_MGI):'p2_MGI'=evalf(%,2);pvT2:=subs(dat,evalf(subs(dat,pv(T2)))):pvT2_:=evalf(%,2);

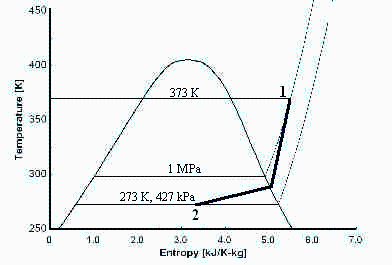
i.e. con el modelo de gas ideal, al enfriar esos 55 g de NH3 a V=cte desde 373 K hasta 273 K, la presión bajaría desde 1 MPa hasta 0,73 MPa, pero en esas condiciones no puede existir el gas en equilibrio porque sería p>pv (o T<Tvp).

La evolución será un enfriamiento isocoro y por tanto a densidad constante, desde el punto inicial gaseoso, hasta quedar bifásico a 0 ºC con una fracción másica de vapor de:

>	eq12:=v1=x2*vv2+(1-x2)*vl2;eq12:='R*T1/p1=x2*R*T2/pvT2+(1-x2)/rho';eq12_:=subs(dat,eq12):evalf(%,2);x2_:=solve(eq12_,x2):'x2'=evalf(%,2);

i.e. 58%wt de vapor y 42%wt de líquido. Con el gráfico del NH3 se obtiene x2=0,55.

e) Calor evacuado en el proceso anterior.

>	eqBE:=DE=W+Q;W:=0;Q:=DU;Q:=D(H-p*V);Q:=DH-V*Dp;Q:=m*Dh-V*Dp;Q:=m*(h2-h1)-V*(p2-p1);Q:=m*(hl2+x2*hlv2-h1)-V*(p2-p1);

Con el modelo de sustancia perfecta (gas perfecto, líquido perfecto y aproximación lineal de hlv(T), con href=0 y sref=0 para líquido en el punto triple:

>	hl2:=c*(T2-T[f]);h2l_:=subs(dat,%):'h2l'=evalf(%,2);hlv2:=h[lv0]-(c-c[p])*(T2-T[f]);hlv2_:=subs(dat,%);h1:=h[lv0]+c[p]*(T1-T[f]);h1_:=subs(dat,%):'h1'=evalf(%,2);Q_:=subs(m=m__,x2=x2_,p2=pvT2,dat,Q):'Q'=evalf(%,2);

i.e., salen 37 kJ del sistema.

Con el gráfico, h2=-50 kJ/kg y h1=700 kJ/kg.

>	'm'=0.060*kg_,'x2'=0.55,h1=700e3*J_/kg_,h2=-50e3*J_/kg_;Q_:=subs(m=0.06*kg_,x2=0.55,h1=700e3*J_/kg_,h2=-50e3*J_/kg_,p2=pvT2_,dat,Q):'Q'=evalf(%,2);

i.e. realmente salen 39 kJ del interior (digamos 39+/-3 kJ).

f) De las familias de curvas que aparecen en el diagram p-h sólo una de ellas bastaría para obtener las otras; ¿cuál de ellas? ¿Cómo se obtendrían las densidades en función de la familia anterior?

La que corresponde a un potencial termodinámico es h(s,p), es decir, la familia de isoentrópicas, ya que dh=Tds+vdp.

La densidad es el inverso de v, que se obtendría de la familia de isoentrópicas como:

>	v:=Diff(h,p)[s];

>

i.e., haciendo gráficamente el límite del cociente incremental Dh/Dp a lo largo de una isoentrópica.