| > | restart:#"m04_p25" |
Dentro de las acciones contra el cambio climático, una de las propuestas contra el calentamiento global por efecto invernadero es la de quitar dióxido de carbono de la atmósfera y almacenarlo en las profundidades marinas. En las tablas adjuntas se resumen algunos datos de interés al respecto. Se pide:
a) Estimar la subida del nivel medio del mar por la dilatación térmica debida a un incremento medio de temperatura (para los valores numéricos puede considerarse una profundidad media de 3 km, una temperatura media del agua de 8 ºC, y un incremento de 0,5 ºC en el siglo XX).
b) Determinar el coeficiente de expansión térmica isobárico del dióxido de carbono a partir de los valores de la tabla.
c) Estimar a quĂ© profundidad del mar habrĂa que depositar el diĂłxido de carbono para que no tuviese flotabilidad.
Tabla 1. Datos del agua de mar.
T [ÂşC] 0 10 20
[kg/m3] 1028 1027 1025
c [m/s] 1450 1490 1520
Tabla 2. Datos del diĂłxido de carbono (a la presiĂłn de saturaciĂłn).
T [ÂşC] -56 -23 -3 7 17 27 31
[kg/m3] 1180 1050 950 880 800 680 470
c [m/s] 1030 730 550 460 360 250 0
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): |
| > | su1:="H2O":su2:="CO2":dat:=[z0=3000*m_,Tw0=(8+273)*K_,DTxx=0.5*K_]:tw:=[0,10,20]:'t[w]'=tw*'ÂşC';Tw:=seq(tw[i]+273,i=1..3):'T[w]'=Tw*K_;rhow:=[1028,1027,1025]:'rho[w]'=rhow*kg_/m_^3;cw:=[1450,1490,1520]:'c[w]'=cw*m_/s_;Tco2:=expand([217,250,270,280,290,300,304]*K_):tco2:=seq(Tco2[i]/K_-273,i=1..7):'t[CO2]'=tco2*'ÂşC';'T[CO2]'=Tco2;rhoco2:=[1179,1047,947,884,805,680,466]:'rho[CO2]'=rhoco2*kg_/m_^3;cco2:=[1030,730,550,460,365,250,0]:'c[CO2]'=cco2*m_/s_; |
Esquema:
| > |
| > |
Eqs. constit.:
| > | Wdat:=get_gas_data(su1),get_liq_data(su1):CO2dat:=get_gas_data(su2),get_liq_data(su2):dat:=op(dat),Const,SI2,SI1:get_pv_data(su2): |
a) Estimar la subida del nivel medio del mar por la dilatación térmica debida a un incremento medio de temperatura (para los valores numéricos puede considerarse una profundidad media de 3 km, una temperatura media del agua de 8 ºC, y un incremento de 0,5 ºC en el siglo XX).
La estimaciĂłn para el siglo XXI es de un incremento medio entre 2 ÂşC y 4 ÂşC; si fuese de 2 ÂşC, serĂa el máximo desde la RevoluciĂłn NeolĂtica, y si fuese de 4 ÂşC, serĂa volver al clima de hace 200 millones de años, cuando los dinosaurios.
En realidad, estos valores de incrementos de temperatura se refieren a la temperatura media del aire a nivel del mar, que pueden ser representativos también de los incrementos de temperatura del agua de mar en superficie. Sin embargo, se piensa que los valores de incrementos de temperatura global de todo el océano sean bastante menores (tal vez la décima parte).
Usamos el modelo de lĂquido dilatable perfecto (i.e. sin considerar el efecto de la presiĂłn), y un valor representativo del coeficiente de dilataciĂłn en el intervalo dado.
| > | eqMLD:=rho=rho0*(1-alpha*(T-T0));eq1:=alpha=-Diff(rho,T)/rho;eq1_:=alpha=(-(rhow[3]-rhow[1])/rhow[2])/(Tw[3]-Tw[1])/K_:evalf(%,2);eqBM:=rho0*V0=rho0*V0+rho0*A*Dz-Drho*V0;Drho:=rho0*alpha*DT;eqBM:=0=rho0*(V0/z0)*Dz-Drho*V0;Dz:=z0*alpha*DT;Dz_:=subs(eq1_,DT=DTxx,dat,Dz):'Dz'=evalf(%,2);Drho:='Drho': |
i.e., del orden de 20 cm. La incertidumbre de este resultado es grande debido a la no linealidad de alpha, pero inferior a la asociada al DT (el efecto de las variaciones de presión siempre será despreciable). Nótese que interviene la dilatación volumétrica y no meramente la dilatación lineal (que es 1/3 de aquélla).
Aunque el efecto directo del calentamiento del mar sobre su nivel no sea importante (el efecto de los hielos es mucho mayor), sà resulta detectable y puede servir para correlacionar modelos climáticos.
b) Determinar el coeficiente de expansión térmica isobárico del dióxido de carbono a partir de los valores de la tabla.
Como las variaciones de presiĂłn asociadas a los datos del CO2 serán muy grandes (desde la presiĂłn del punto triple a la del punto crĂtico, mientras que en el agua era un intervalo muy estrecho), vamos a tenerlas en cuenta.
| > | eqGEN:=dv=alpha*v*dT-kappa*v*dp;eqGEN:=-d(rho)/rho=alpha*dT-kappa*dp;eq2:=alpha=-Diff(rho,T)[sat]/rho-kappa*Diff(p,T)[sat];eq2:=alpha=-(Drho/DT)/rho+kappa*dp_dT_sat;eqc:=c=sqrt(1/(rho*kappa));kappa:=1/(rho*c^2);kappa_:=seq(1/(rhoco2[i]*cco2[i]^2),i=1..6)/Pa_:'kappa'=evalf(%,2); |
![alpha = `+`(`-`(`/`(`*`((Diff(rho, T))[sat]), `*`(rho))), `-`(`*`(kappa, `*`((Diff(p, T))[sat]))))](images/np25_23.gif) |
La pendiente de la curva de presión de vapor la obtenemos de la correlación de Antoine, que es más precisa que la ecuación integrada de Clapeyron en este intervalo tan grande.
| > | pvAnt:=p0u*exp(A-B/(T+C));dp_dT_sat:=diff(pvAnt,T);dp_dT_sat:=diff(pv(T),T):eq2_:='alpha[i]=-((rhoco2[i+1]-rhoco2[i-1])/rhoco2[i])/(Tco2[i+1]-Tco2[i-1])-kappa*dp_dT_sat';eq2__:=[seq(subs(T=Tco2[i],rho=rhoco2[i]*kg_/m_^3,c=cco2[i]*m_/s_,dat,eq2_),i=2..6)]:evalf(%,2); |
c) Estimar a quĂ© profundidad del mar habrĂa que depositar el diĂłxido de carbono para que no tuviese flotabilidad.
Tomamos la densidad del agua uniforme porque se ve que varĂa poco, e.g. rho(10 ÂşC). El CO2 quedará a la misma tempertura, luego T[CO2]=10 ÂşC. A esa temperatura, la presiĂłn de equilibrio bifásico es:
| > | T[eq]:=TKC(tw[2]);p[eq]:=p[v,CO2,Teq];peq_:=subs(dat,evalf(subs(dat,pv(Tw[2]*K_)))):'p[v,CO2,Teq]'=evalf(%,2); |
i.e., a 10 ÂşC el CO2 estarĂa lĂquido por debajo de los 450 m de profundidad (gaseoso a menos profundidad), pero la densidad del CO2 lĂquido saturado, de acuerdo con la tabla, es de unos 860 kg/m^3, asĂ que habrá que depositarlo a mucha mayor profundidad para que la compresibilidad en estado lĂquido eleve la densidad desde los 860 kg/m^3 hasta los 1027 kg/m^3..
| > | rhoco2_10_pv_:=evalf(rhoco2[4]+(10-tco2[4])*(rhoco2[5]-rhoco2[4])/(tco2[5]-tco2[4]),2)*kg_/m_^3;rhoco2_10_p:='rhoco2_10_pv*(1+kappa*(p-p[v,CO2,Teq]))';Dp:='(Drho/rho)/kappa';Drho_:=rhow[2]*kg_/m_^3-rhoco2_10_pv_;kappa_:=1/(rhoco2_10_pv_*(cco2[4]*m_/s_)^2);Dp_:=subs(dat,(Drho_/rhoco2_10_pv_)/kappa_):'Dp'=evalf(%,2);p_:=peq_+Dp_:'p'=evalf(%,2); |
que corresponde a una profundidad de:
| > | eqBH:=p=p0+rho*g*z;z[eq]:=(p-p0)/(rho*g);zeq_:=subs(dat,(p_-p0)/(rhow[2]*(kg_/m_^3)*g)):'z[eq]'=evalf(%); |
i.e., como mĂnimo hay que depositarlo a unos 4000 m de profundidad. Pero la incertidumbre puede ser muy grande (por ejemplo, no parece razonable tomar 10 ÂşC a esas profundidades). Mejor resulatado se obtendrĂa, y con muchĂsimo menos esfuerzo, buscando en un diagrama de propiedades del CO2 el punto de corte de la isoterma correspondiente (10 ÂşC, o mejor 2 ÂşC a las profundidades esperadas) con la isocora correspondiente (1027 kg/m^3, o mejor 1045 kg/m^3 a 2 ÂşC y a las presiones esperadas); se obtiene una presiĂłn de unos 30 MPa que corresponden a unos 3000 m de profundidad).
| > | Dp:='Dp':rhow3500:='rhow0*(1+kappa*Dp)';kappa_:=1/(rhow[1]*(cw[1]*m_/s_)^2);rhow3500_:=subs(z=3500*m_,dat,rhow[1]*(1+kappa_*rhow[2]*g*z))*kg_/m_^3;z[eq]:=evalf(subs(dat,30e6*Pa_/(1030*(kg_/m_^3))/(9.8*m_/s_^2))); |
En Hawai y en Noruega se han hecho ensayos para depositar CO2 lĂquido a 3000 m de profundidad en el mar, que se suspendieron por motivos medioambientales, pero sigue adelante un programa en la BahĂa de Monterrey (California). El secuestro o captura del CO2 atmosfĂ©rico, para evitar el calentamiento global por incremento antropogĂ©nico de la concentraciĂłn de gases de efecto invernadero (en inglĂ©s: CO2 capture or CO2 sequestration), es un problema que habrá que resolver en el prĂłximo futuro, tal vez almacenándolo en cavernas subterráneas (el problema no es tan abismal como pudiera parecer porque se trata de eliminar el CO2 generado desde la RevoluciĂłn Industrial hasta el 2100 o asĂ, ya que luego no habrá combustibles fĂłsiles que quemar.
Otra curiosidad serĂa calcular el efecto de la compresibilidad del agua sobre la altura del mar.
Con el modelo de lĂquido compresible perfecto, DV/V-kappa*Dp, y como el Dp es variable habrĂa que integrar, pero como varĂa linealmente, basta tomar el Dp medio (a 1500 m de profundidad).
| > | DV:='DV':Dz:='Dz':eqCompr:=DV/V='-kappa*Dp';eqCompr:=DV/V='-kappa*Dp[mean]';eqCompr:=Dz/z0='-kappa*rho*g*z0/2';kappa_:=1/(rhow[2]*(cw[2])^2)/Pa_:'kappa'=evalf(%,2);Dz_:=subs(dat,Wdat,-z0*kappa_*rho*g*z0/2); |
i.e. el nivel del mar está 20 m más bajo, debido a la compresiĂłn por su propio peso, de lo que estarĂa sin peso o siendo indeformable.
| > |
Las gráficas de las funciones que han intervenido son:
Densidades del CO2 y del agua.
| > | plot(subs(SI0,[[seq([Tw[i]/K_,rhow[i]],i=1..3)],[seq([Tco2[i]/K_,rhoco2[i]],i=1..7)]]),T_K=200..305,'rho_kg_m3'=0..1100); |
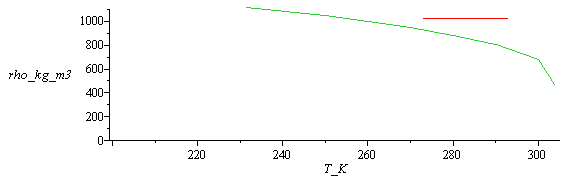 |
Velocidad del sonido en el CO2 y en el agua.
| > | plot(subs(SI0,[[seq([Tw[i]/K_,cw[i]],i=1..3)],[seq([Tco2[i]/K_,cco2[i]],i=1..7)]]),T_K=200..305,'c_m_s'=0..1500); |
 |
Presión de vapor del CO2 (la del agua es muy pequeña en ese intervalo, del orden de 1 kPa).
| > | plot(subs(CO2dat,SI0,[[[T[f],pv(T[f])/1e6],[T[f],pv(T[cr])/1e6]],pv(T_K)/1e6]),T_K=200..305,pv_MPa=0..10); |
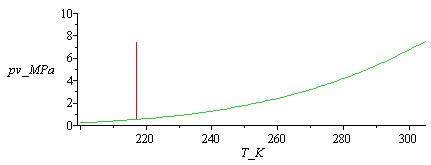 |
Coeficientes de compresibilidad del CO2 y del agua.
| > | kappa:=1/(rho*c^2);kappa_:=evalf(seq(1/(rhoco2[i]*cco2[i]^2),i=1..6)):'kappa[CO2]'=seq(evalf([kappa_][i],2)/Pa_,i=1..6);kappa__:=evalf(seq(1/(rhow[i]*cw[i]^2),i=1..3)):'kappa[agua]'=seq(evalf([kappa__][i],2)/Pa_,i=1..3);plot([[seq([Tco2[i]/K_,kappa_[i]],i=1..6)],[seq([Tw[i],kappa__[i]],i=1..3)]],T_K=200..305,'kappa_1_Pa'=1e-10..1e-8); |
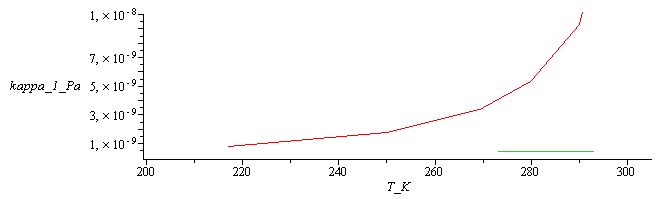 |
Coeficiente de dilatación del CO2 y del agua. Se va a dibujar alpha[CO2] obtenido por 3 procedimientos: en rojo el cálculo completo centrado, en amarillo el cálculo sin efectos de presión, avanzado, y en verde el cálculo completo avanzado.
| > | eq3:='alpha[i]=-((rhoco2[i+1]-rhoco2[i])/rhoco2[i])/(Tco2[i+1]-Tco2[i])+kappa*dp_dT_sat';eq3_:=[seq(subs(T=Tco2[i],rho=rhoco2[i]*kg_/m_^3,c=cco2[i]*m_/s_,dat,alpha[i]=op(1,op(2,eq3))),i=1..6)]:evalf(%,2);eq3__:=[seq(subs(T=Tco2[i],rho=rhoco2[i]*kg_/m_^3,c=cco2[i]*m_/s_,dat,eq3),i=1..6)]:evalf(%,2);alphaw_:=seq((-(rhow[i+1]-rhow[i])/rhow[i])/(Tw[i+1]-Tw[i]),i=1..2):'alpha[agua]'=evalf(expand([%]/K_),2);plot(subs(SI0,[[seq([Tco2[i],rhs(eq2__[i])],i=1..5)],[seq([Tco2[i],rhs(eq3_[i])],i=1..6)],[seq([Tco2[i],rhs(eq3__[i])],i=1..6)],[seq([Tw[i],alphaw_[i]],i=1..2)]]),T_K=200..305,'alpha_1_K'=0..0.01); |
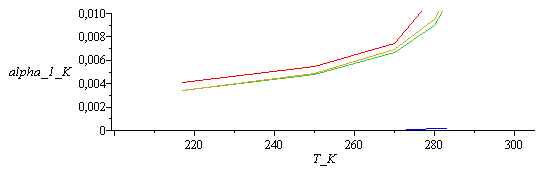 |
Se ve que, contrariamente a lo que se pensĂł al principio, los efectos de la presiĂłn no son importantes (excepto cerca del punto crĂtico).
| > |