>	restart:#"m03_p19"

Considérese una planta de potencia nuclear de 950 MW en la que el núcleo del reactor se mantiene a 320 ºC. Se pide:
a) Valores mínimos de la potencia térmica que debe generar el núcleo del reactor, y de la potencia térmica que es preciso evacuar.
b) Considerar que con el calor del núcleo se calienta una corriente de agua a presión desde la temperatura ambiente hasta 5 ºC por debajo de la del núcleo, y calcular el gasto másico necesario. Indicar la precisión esperada del modelo usado.
c) Trabajo máximo obtenible de la corriente de agua a la salida del núcleo.
d) Caudal de agua de refrigeración necesario para que éste no aumente más de 8 ºC su temperatura.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):

>	su1:="H2O":dat:=[Wdot=950e6*W_,T1=(320+273)*K_,DT1=5*K_,DT2=8*K_];

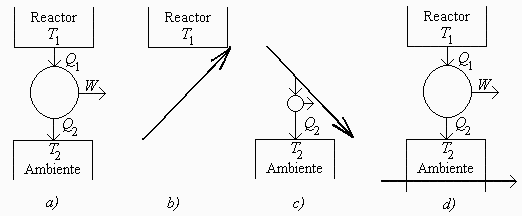
Esquema:

>

>

Ecs. const.:

>	dat:=op(dat),get_liq_data(su1),Const,SI2,SI1:

a) Valores mínimos de la potencia térmica que debe generar el núcleo del reactor, y de la potencia térmica que es preciso evacuar.

Se trata de un motor térmico que genera 950 MW de potencia mecánica a partir de la potencia térmica que recibe del reactor nuclear.

El mínimo será el correspondiente al rendimiento de Carnot.

>	eqBE:=Wdot=Q1dot-Q2dot;eqCarnot:=eta[max]=1-T2/T1;eqT0:=T2=T0;subs(dat,%);eqBEmin:=Wdot=Q1dot*eta[max];'Wdot'=subs(dat,Wdot);Q1dot_:=subs(eqCarnot,eqT0,solve(eqBEmin,Q1dot));'Q1dot'=subs(dat,%);Q2dot_:=solve(eqBE,Q2dot);Q2dot__:=subs(Q1dot=Q1dot_,eqCarnot,eqT0,dat,%);

i.e. el reactor debe dar como mínimo 1850 MW y la refrigeración al ambiente ha de ser como mínimo 900 MW.

b) Considerar que con el calor del núcleo se calienta una corriente de agua a presión desde la temperatura ambiente hasta 5 ºC por debajo de la del núcleo, y calcular el gasto másico necesario. Indicar la precisión esperada del modelo usado.

>	eqBE:=Q1dot=mdot*c*(T1-DT1-T0);mdot_:=subs(Q1dot=Q1dot_,dat,solve(%,mdot));

i.e. hay que bombear por lo menos 1470 kg/s de agua.

Se ha usado el modelo de líquido perfecto con c=4200 J/(kg*K), cuando en realidad c crece bastante con T (a 320 ºC vale 6200 J/(kg*K), con un valor medio de unos 4800 J/(kg*K)). Con la presión apenas varía.

c) Trabajo máximo obtenible de la corriente de agua a la salida del núcleo.

Será la exergía de la corriente.

>	Wmax:=mdot*(Dh-T0*Ds);Wmax:=mdot*(c*(T1-T0)-T0*c*ln(T1/T0));Wmax_:=subs(dat,evalf(subs(mdot=mdot_,dat,%)));

i.e. Wmax=600 MW, de donde se concluye que el núcleo ha de dar más calor, y ha de circular más agua por él.

d) Caudal de agua de refrigeración necesario para que éste no aumente más de 8 ºC su temperatura.

>	eqBE:=Q2dot=mdot*c*DT2;mdot_:=subs(Q2dot=Q2dot__,dat,solve(%,mdot));

i.e., como mínimo 27 m3/s.

>