>	restart:#"m3_p09"

Se dispone de dos vasos conteniendo un litro de agua cada uno en presencia de una atmsfera a 20 C. Se desea elevar la temperatura de una de las masas de agua hasta la de ebullicin. Se pide:
a)  Estimar la presin ambiente en el laboratorio sabiendo que est a unos 670 m de altitud sobre el nivel del mar.
b)  Determinar la temperatura de ebullicin y la energa que es preciso comunicar al agua para llegar a ella.
c)  Si se realizase el calentamiento directamente con una resistencia elctrica de 120 W, estimar el tiempo que se tardara, y definir y calcular el rendimiento energtico en este caso.

d) Trabajo mnimo necesario.
e)  Estimar el flujo mximo de prdida de calor al ambiente suponiendo que el coeficiente global de transmisin de calor desde el agua caliente al ambiente es de 10 W/(m2K) y un rea tpica del vaso.
f)  Suponiendo que se fuera a utilizar una bomba de calor funcionando entre la temperatura ambiente y la de ebullicin, calcular el trabajo mnimo necesario y el rendimiento energtico.
g)  Calcular la potencia que consumira la bomba si tardase en calentar el mismo tiempo que la resistencia elctrica.
h)  Razonar la validez prctica del resultado anterior.
i)  Razonar cuantitativamente la posibilidad de que la bomba de calor anterior hubiera tomado el calor del agua fra, estimando el estado final de sta..

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="H2O":su2:="Aire":dat:=[m1=1*kg_,m2=1*kg_,T0=(20+273)*K_,z1=670*m_,P=120*W_,h[a]=10*W_/(m_^2*K_)];

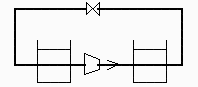
Esquema:

>

>

Eqs. const.:

>	eqETl:=eq1_15;eqEEl:=eq1_17;eqETg:=eq1_12;eqEEg:=eq1_16;ldat:=get_liq_data(su1):gdat:=get_gas_data(su2):dat:=op(dat),Const,gdat,ldat,SI2,SI1:get_pv_data(su1):

a)  Estimar la presin ambiente en el laboratorio sabiendo que Madrid est a unos 670 m de altitud sobre el nivel del mar.

Suponiendo que la densidad del aire no vara mucho en los 670 m (el valor verdadero es 94 kPa):

>	eqBF:=diff(p(z),z)=-rho*g;rho_:=subs(p=p0,T=T0,dat,rhs(eqETg)):'rho'=evalf(%,4);p1:=p0-rho*g*z1;p1_:=subs(rho=rho_,dat,p1):'p1'=evalf(%/(1000*Pa_/kPa_));rho_:=subs(p=p1_,T=T0,dat,rhs(eqETg)):'rho'=evalf(%,4);p1_:=subs(rho=rho_,dat,p1):'p1'=evalf(%/(1000*Pa_/kPa_));

b)  Determinar la temperatura de ebullicin y la energa que es preciso comunicar al agua para llegar a ella.

>	Tb1_:=solve(p1_=pv(T),T);Tb1_C:=TKC(Tb1_);eq1:=subs(m=m1,DT=Tb1_-T0,dat,eqEEl):'DU'=evalf(subs(eq1,DU)/(1000*J_/kJ_));

c)  Si se realizase el calentamiento directamente con una resistencia elctrica de 120 W, estimar el tiempo que se tardara, y definir y calcular el rendimiento energtico en este caso.

>	eq2:=DU=P*t1;t1_:=subs(dat,rhs(eq1)/P);eta[e]:=Q/W;eta[e]:=DU/(P*t);eta[e_]:=1;

d) Trabajo mnimo necesario.

>	DSuniv:=0;eq3:=DSuniv=m1*c*ln(Tb1/T0)+Q0/T0;Wmin:=m1*c*(Tb1-T0)-T0*m1*c*ln(Tb1/T0);Wmin_:=subs(dat,evalf(subs(Tb1=Tb1_,dat,Wmin))):'Wmin'=evalf(%/(1000*J_/kJ_));

e)  Estimar el flujo mximo de prdida de calor al ambiente suponiendo que el coeficiente global de transmisin de calor desde el agua caliente al ambiente es de 10 W/(m2K) y A un rea tpica del vaso.

>	A:=6*(m1/rho)^(2/3);A_:=subs(dat,SI0,A)*m_^2;Q1dot:='h[a]*A*(T1-T0)';Q1dot_:=subs(dat,h[a]*A_*(Tb1_-T0));

f)  Suponiendo que se fuera a utilizar una bomba de calor funcionando entre la temperatura ambiente y la de ebullicin, calcular el trabajo mnimo necesario y el rendimiento energtico.

>	eta[B]:=T1/(T1-T0);eta[B_]:=subs(T1=Tb1_,dat,eta[B]);eta[B]:=Q1/W;Q1:=DU;Q1_:=rhs(eq1):'Q1'=evalf(%/(1000*J_/kJ_));W_:=Q1_/eta[B_]:'W'=evalf(%/(1000*J_/kJ_));

g)  Calcular la potencia que consumira la bomba si tardase en calentar el mismo tiempo que la resistencia elctrica.

>	P[B]:=W/t;P[B_]:=subs(dat,W_/t1_);

h)  Razonar la validez prctica del resultado anterior.

No es prctico porque no tiene en cuenta los saltos trmicos necesarios para una Qdot finita.

Adems habra que poner un buen ventilador en el lado del aire.

i)  Razonar cuantitativamente la posibilidad de que la bomba de calor anterior hubiera tomado el calor del agua fra, estimando el estado final de sta.

>	Q2:=Q1-W;Q2_:=Q1_-W_:'Q2'=evalf(%/(1000*J_/kJ_));T2:=T0-Q2/(m2*c);T2_:=subs(Q2=Q2_,dat,T2);

pero como transpasa un cambio de fase no vale. Congelara parte del agua.

>	Q20:=m2*c*(T0-T[f]);Q20_:=subs(dat,Q20):'Q20'=evalf(%/(1000*J_/kJ_));m[ice]:=(Q2-Q20)/h[sl0];m[ice_]:=subs(dat,(Q2_-Q20_)/h[sl0]):'m[ice]'=evalf(%*1000*g_/kg_);

>