>	restart:#"m02_p18"

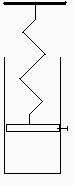
Dentro de un cilindro de 0,1 m2 de sección, un émbolo superior de 40 kg encierra una masa de un gas cuya capacidad térmica específica a presión constante y su masa molar son, respectivamente cp=1,92 kJ/(kg•K} y M=42 kg\kmol. El émbolo, cuyas superficies en contacto con el gas confinado y con el aire ambiente son adiabáticas, se encuentra unido a un punto fijo exterior por medio de un muelle perfectamente elástico cuya constante elástica es 225 kN\/m. Inicialmente el gas se encuentra a temperatura ambiente y a una presión de 2,25 MPa ocupando un volumen de 50 L, el émbolo se halla, también a temperatura ambiente y anclado al cilindro y el muelle en su longitud natural. A partir de estas condiciones iniciales se quitan los anclajes del émbolo y tras un proceso lo suficientemente rápido como para que el proceso de expansión subsiguiente del gas pueda considerarse adiabático, se alcanza el equilibrio mecánico. Después se deja que todo el dispositivo se atempere. Suponiendo que la energía mecánica disipada por la fricción entre el cilindro y el émbolo se concentra en el émbolo, sabiendo que las condiciones del ambiente son 300 K y 100 kPa y que la fuerza de fricción en reposo se considera despreciable, se pide:

a) Determinar la masa de gas confinado en el cilindro.

b) Establecer las ecuaciones que determinan la temperatura, la presión, y el volumen ocupado por el gas al alcanzarse el equilibrio mecánico.

c) Resolver el sistema anterior dando los valores de la temperatura, de la presión, y del desplazamiento del émbolo al alcanzarse el equilibrio mecánico.

d) Calcular la energía disipada por la fricción entre el émbolo y el cilindro.

e) Calcular el calor neto intercambiado con el ambiente en el proceso de atemperamiento.

f) Calcular la producción el proceso global descrito.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	dat:=[A=0.1*m_^2,mE=40*kg_,cp=1920*J_/(kg_*K_),M=0.042*kg_/mol_,k=0.225e6*N_/m_,T0=300*K_,p1=2.25e6*Pa_,V1=0.05*m_^3];

>	datgas:=R=subs(dat,Const,R[u]/M),gamma=subs(dat,Const,cp/(cp-R[u]/M));dat:=op(dat),datgas,Const,SI2,SI1:

a) Determinar la masa de gas confinado en el cilindro.

>	eqMGI:=m=p1*V1/(R*T0);eqMGI_:=subs(dat,%);eqz:=z=V/A;eqz1:=subs(V=V1,dat,%);

	(1)

b) Establecer las ecuaciones que determinan la temperatura, la presión y el volumen ocupado por el gas al alcanzarse el equilibrio mecánico.

>	eq1:=p2*A=p0*A+mE*g+k*(z2-z1);eq2:=p2*z2^gamma=p1*z1^gamma;

	(2)

c) Resolver el sistema anterior dando los valores de la temperatura, de la presión y del desplazamiento del émbolo al alcanzarse el equilibrio mecánico.

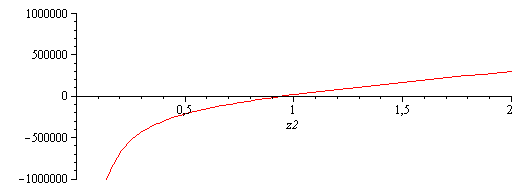
>	eq2_:=subs(z1=rhs(eqz1),dat,SI0,eq2);eq1_:=subs(z1=rhs(eqz1),p2=solve(eq2_,p2),dat,SI0,eq1);plot(rhs(%)-lhs(%),z2=0..2,-1e6..1e6);z2_:=fsolve(eq1_,z2)*m_;p2_:=evalf(subs(z2=z2_,dat,SI0,solve(eq2_,p2)))*Pa_;T2=p2*V2/(m*R);T2_:=subs(eqMGI_,dat,p2_*A*z2_/(m*R));

	(3)

i.e. el émbolo sube de 0,50 m a 0,95 m, la presión baja de 2,25 MPa a 1,11 MPa, y la temperatura baja de 300 K a 279 K.

d) Calcular la energía mecánica disipada por la fricción entre el émbolo y el ciclindro.

Será Emdf=mE*cE*DTE, en el balance energético global entre 1 y 2:

>	eqBE12:=m*(cp-R)*(T2-T1)+mE*cE*DTE+mE*g*(z2-z1)+(1/2)*k*(z2-z1)^2=0-p0*A*(z2-z1);Emdf12:=subs(z2=z2_,p2=p2_,T2=T2_,z1=rhs(eqz1),T1=T0,eqMGI,dat,-p0*A*(z2-z1)-m*(cp-R)*(T2-T1)-mE*g*(z2-z1)-(1/2)*k*(z2-z1)^2);

	(4)

i.e. se disipan 42 kJ por fricción.

e) Calcular el calor neto intercambiado con el ambiente en el proceso de atemperamiento

De 1 a 3, sea Q0 el calor que recibe el ambiente.

>

eq1:=p3*A=p0*A+mE*g+k*(z3-z1);eq2:=p3*A*z3=m*R*T0;eq1_:=subs(p3=solve(eq2,p3),z1=rhs(eqz1),T1=T0l,eqMGI,dat,SI0,eq1);z3_:=fsolve(%,z3=0.5..2)*m_;p3_:=subs(z3=z3_,eqMGI,dat,SI0,solve(eq2,p3))*Pa_;eqBE13:=m*(cp-R)*(T3-T1)+Q0+mE*g*(z3-z1)+(1/2)*k*(z3-z1)^2=0-p0*A*(z3-z1);Q0_:=subs(z3=z3_,p3=p3_,T3=T0,z1=rhs(eqz1),T1=T0,eqMGI,dat,-p0*A*(z3-z1)-m*(cp-R)*(T3-T1)-mE*g*(z3-z1)-(1/2)*k*(z3-z1)^2);

	(5)

i.e. el ambiente no recibe, sino que cede, 30 kJ.

f) Calcular la producción de entropía en el proceso global descrito

>	Sgen_univ=DS_univ;DS_univ:=DSgas+DSamb;DSgas:=-m*R*ln(p3/p1);DSgas_:=subs(eqMGI,dat,evalf(subs(dat,-m*R*ln(p3_/p1))));DSamb:=Q0/T0;DSamb_:=subs(dat,Q0_/T0);DS_univ_:=DSgas_+DSamb_;

	(6)

i.e. Sgen=150 J/K.

>