>	restart:#"m02_p16"

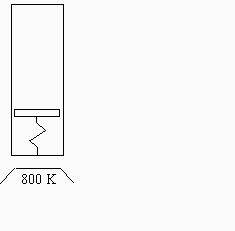
Dentro de un cilindro vertical de 60 cm de diámetro hay un émbolo de 10 kg que separa dos masas de gas. Inicialmente todo está a 15 ºC, la parte de abajo ocupa 100 litros y contiene 0,2 kg de nitrógeno, y la de arriba ocupa 300 litros y está a 90 kPa. El émbolo está unido a la base inferior mediante un muelle de constante 250 kN/m. Considérese que todas las superficies son adiabáticas excepto la de la base inferior del cilindro, y que se pone en contacto térmico con una fuente a 800 K y se deja que se alcance el equilibrio. Se pide:

a) Presión inicial del nitrógeno.

b) Presión final del nitrógeno.

c) Generación de entropía en el proceso.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aire":su2:="N2":dat:=[D=0.6*m_,mE=10*kg_,T0=(15+273.15)*K_,V_N1=0.1*m_^3,mN=0.2*kg_,V_A1=0.3*m_^3,p_A1=90e3*Pa_,k=0.25e6*N_/m_,T2=800*K_];

Ecs. const.:

>	Adat:=get_gas_data(su1):Ndat:=get_gas_data(su2):dat:=op(dat),A=evalf(subs(dat,Pi*D^2/4)),Const,SI2,SI1:

a) Presión inicial del nitrógeno.

>

eqmA:=mA=p_A*V_A/(R*T_A);eqmA1:=subs(p_A=p_A1,V_A=V_A1,T_A=T0,Adat,dat,%);eqmN:=mN=p_N*V_N/(R*T_N);eqN1:=p_N1=subs(V_N=V_N1,T_N=T0,Ndat,dat,solve(%,p_N));eqzN:=zN=V_N/A;eqzN1:=zN1=subs(V_N=V_N1,dat,rhs(%));eqzn:=p_N*A=p_A*A+mE*g+k*(z-zn);eqzn_:=zn=subs(eqN1,z=rhs(eqzN1),p_N=rhs(eqN1),p_A=p_A1,dat,solve(%,zn));

	(1)

i.e. 170 kPa. El muelle está inicialmente estitado desde su longitud natural zn=0,26 m hasta los 0,35 m en que está la cara inferior del émbolo (el espesor no influye en el problema).

>

T_N2=T2;eqmA2:=subs(p_A=p_A2,V_A=V_A2,T_A=T_A2,eqmA1,Adat,dat,SI0,eqmA);eqmN2:=subs(p_N=p_N2,V_N=V_N2,T_N=T2,Ndat,dat,SI0,eqmN);eqV:=subs(dat,SI0,V_N1+V_A1=V_N2+V_A2);eqk:=p_N2*A=p_A2*A+mE*g+k*(z2-zn);eqk_:=subs(eqzn_,dat,SI0,%);eqzN2:=z2=V_N2/A;eqzN2_:=subs(dat,SI0,%);eqBE:=p_A2*V_A2^gamma=p_A1*V_A1^gamma;eqBE_:=subs(Adat,dat,SI0,%);sol_:=fsolve({eqmA2,eqmN2,eqV,eqk_,eqzN2_,eqBE_},{z2,p_A2,p_N2,V_A2,V_N2,T_A2},{V_N2=0.11..0.39});

	(2)

Las 6 a la vez no sabe, pero es fácil pasar a una sola ecuación:

>

pA2:=evalf(solve(eqBE_,p_A2));VN2:=solve(eqV,V_N2);eqk__:=subs(p_A2=pA2,eqzN2_,V_N2=VN2,eqk_);pN2:=solve(%,p_N2);eqmN2_:=subs(V_N2=VN2,p_N2=pN2,eqmN2);VA2_:=fsolve(%,V_A2=0.1..0.3)*m_^3;pA2_:=subs(V_A2=VA2_,SI0,pA2)*Pa_;pN2_:=subs(V_A2=VA2_,SI0,pN2)*Pa_;TA2_:=subs(p_A2=pA2_,V_A2=VA2_,SI0,solve(eqmA2,T_A2))*K_;z2_:=subs(dat,V_A2=VA2_,(V_N1+V_A1-V_A2)/A);

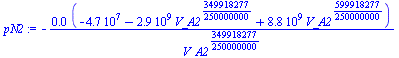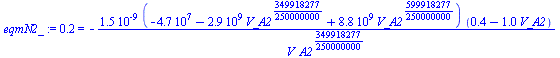	(3)

i.e. el nitrógeno pasa de 170 kPa a 350 kPa, el émbolo sube desde 0,35 m hasta 0,51 m, y el aire pasa a tener 110 kPa y 307 K.

c) Generación de entropía en el proceso:

>

Sgen_univ=DS_univ;DS_univ:=DS_DTR+DS_N+DS_A;DS_DTR:=-Q/T2;DS_N:=mN*(c[p]*ln(T2/T0)-R*ln(p_N2/p_N1));DS_A:=0;eqBEint:=mN*c[vN]*(T2-T0)+mE*g*(V_N2-V_N1)/A+mA*c[vA]*(T_A2-T0)=Q+0;DS_N_:=subs(dat,evalf(subs(Ndat,p_N2=pN2_,eqN1,dat,DS_N)));eqBEint_:=subs(c[vN]=c[v],Ndat,c[vA]=c[v],Adat,V_N2=V_N1+V_A1-VA2_,T_A2=TA2_,eqmA1,dat,eqBEint);DS_univ_:=subs(dat,Q=solve(eqBEint_,Q),DS_DTR+DS_N_+DS_A);

	(4)

i.e. la entropía se genera por transmisión de calor con salto térmico desde la fuente al nitrógeno, y es igual al aumento de entropía del nitrógeno menos la entropía que le llega de la fuente, o, lo que es lo mismo, la fuente pierde 100 J/K de entropía, el nitrógeno gana 173 J/K, y los demás subsistemas no varían de entropía por ser adiabáticos y sin fricción, luego, la generación es de 73 J/K.

>