>	restart:#"m02_p14"

Dentro de un cilindro vertical de 0,01 m2 de sección hay 0,01 kg de nitrógeno encerrado con un émbolo superior de 5 kg de acero. Considérese la siguiente evolución: 1) mediante las fuerzas apropiadas se obliga al pistón a reducir lentamente en un 10% el volumen ocupado por el gas, y 2) se libera el anclaje y se permite el libre movimiento del émbolo. Se pide:
a) Esquema de la evolución en un diagrama altura-tiempo.
b) Determinar el espesor del émbolo y su altura inicial.
c) Valores p-V-T en los estados de equilibrio considerados.
d) Variación de energía entre los estados antedichos y para todo el ciclo, así como calor y trabajo transferidos entre los sistemas involucrados.

e) Diagrama T-s de la evolución.
f) Variación de entropía y generación de entropía para todos los sistemas entre los estados antedichos y para todo el ciclo.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):

>	su1:="N2":su2:="Acero_inox":dat:=[A=0.01*m_^2,m=0.01*kg_,mE=5*kg_,V2_V1=0.9];

Esquema:

>

>

Ecs. const.:

>	eqET:=subs(eq1_11,eq1_12);eqEE:=eq1_16;gdat:=get_gas_data(su1):sdat:=get_sol_data(su2):rho[acero]:=subs(sdat,rho);dat:=op(dat),Const,gdat,sdat,SI2,SI1:

a) Esquema de la evolución en un diagrama altura-tiempo.

>

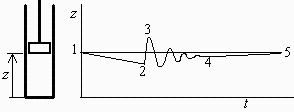
b) Determinar el espesor del émbolo y su altura inicial.

>

eqBF:=mE*diff(z(t),t,t)=(p-p0)*A-mE*g-Ff;eqBFint:=int(mE*diff(z(t),t,t)*diff(z(t),t),t)=Int((p-p0)*A-mE*g-Ff,z);T1:=T0:T2:=T0:p1:=p0+mE*g/A;p1_:=subs(dat,p1):'p1'=evalf(%,3);V1:=solve(subs(p=p1,T=T1,eqET),V);V1_:=subs(dat,subs(p1=p1_,dat,V1)):'V1'=evalf(V1_,2);z1_:=subs(dat,V1_/A):'z1'=evalf(z1_,3);e_:=mE/(rho*A);e__:=subs(dat,e_):'e'=evalf(e__,2);

b) Valores p-V-T en los estados de equilibrio considerados, numerándolos convenientemente.

>

V2_:=subs(dat,dat,V1*V2_V1):'V2'=evalf(V2_,2);p2:=solve(subs(T=T2,V=V2_,eqET),p):p2_:=subs(dat,dat,p2):'p2'=evalf(%,3);z2_:=subs(dat,V2_/A):'z2'=evalf(z2_,3);DU12:=0;W12:=Int(-p,V='V1..V2');W12:='Int(-m*R*T0/V,V=V1_..V2_)';W12_:=evalf(subs(dat,SI0,value(W12)))*J_:'W12'=evalf(W12_,2);Q12:='DU12-W12';Q12_:=DU12-W12_:'Q12'=evalf(Q12_,2);Fdedo:='(m*R*T0/V-p0)*A-mE*g';Wdedo:='Int(-Fdedo/A,V=V1..V2)';Wdedo_:=subs(dat,int(expand(subs(dat,V=V*m_^3,-Fdedo/A*m_^3)),V=V1_/m_^3..V2_/m_^3)):'Wdedo'=evalf(Wdedo_,2);Watm_:=subs(mE=mE_,dat,p0*A*(z1_-z2_)):'Watm'=evalf(Watm_,2);WE_:=subs(dat,mE*g*(z1_-z2_)):'WE'=evalf(WE_,2);Wneto_:=W12_-Watm_-WE_:'Wneto'=evalf(Wneto_,2);

De 2 a 3 integrando el balance de fuerzas y resolviendo a mano.

>

eqBE23:=0='p2*z2^gamma*(z3^(1-gamma)-z2^(1-gamma))*A/(1-gamma)-(p0*A+mE*g)*(z3-z2)';eqBE23_:=subs(z2=z2_,dat,SI0,eqBE23):evalf(%,4);z3aux:=2*z1-z2;z3aux_:=evalf(2*z1_-z2_,3);f(z)=subs(z3=z3aux_/m_,rhs(eqBE23_)):evalf(%,2);z3aux_:=0.850*m_;f(z)=subs(z3=z3aux_/m_,rhs(eqBE23_)):evalf(%,2);z3=0.850*m_;plot({2910-1891/z^0.4-1049*z,rhs(subs(z3=z,eqBE23_))},z=0..1,`f(z)`=-5..5,numpoints=100,tickmarks=[10,3]);

De 2 a 3, pero usando el balance energético.

>

eqBE23:=0=rhs(eqBFint);eqBE23:=m*c[v]*(T3-T2)=-p0*A*(z3-z2)-mE*g*(z3-z2);eqBE23_:=subs(T3=T2*(z2/z3)^(gamma-1),z2=z2_,dat,SI0,eqBE23):z3_:=fsolve(eqBE23_,z3=z2_/m_+1e-6..1)*m_:'z3'=evalf(z3_,3);T3_:=subs(dat,T2*(z2_/z3_)^(gamma-1)):'T3'=evalf(T3_,3);V3_:=subs(dat,z3_*A):'V3'=evalf(V3_,2);p3_:=subs(dat,m*R*T3_/V3_):'p3'=evalf(p3_/(1000*Pa_/kPa_),2);Q23_:=0;W23_:=subs(dat,m*c[v]*(T3_-T2)):'W23'=evalf(W23_,2);

>	p4_:=subs(dat,p1):'p4'=evalf(%/(1000*Pa_/kPa_),2);z4_:=subs(dat,dat,z2_*(p2/p4_)^(1/gamma)):'z4'=evalf(z4_,3);T4_:=subs(dat,T2*(z2_/z4_)^(gamma-1)):'T4'=evalf(T4_,3);V4_:=subs(dat,z4_*A):'V4'=evalf(V4_,2);Q24_:=0;W24_:=subs(dat,m*c[v]*(T4_-T2)):W24_:=evalf(W24_,2);

>	p5_:=subs(dat,p1):'p5'=evalf(%/(1000*Pa_/kPa_),2);z5_:=z1_:'z5'=evalf(z5_,3);T5_:=subs(dat,T1);V5_:=subs(dat,z5_*A):'V5'=evalf(V5_,2);W45_:=subs(dat,-p5_*(V5_-V4_)):'W45'=evalf(W45_,2);Q45_:=subs(dat,m*c[v]*(T5_-T4_)-W45_):'Q45'=evalf(Q45_,2);

c) Representación de la evolución en el diagrama p-V.

>	plot({[[V1_/m_^3,p1_/Pa_],[V2_/m_^3,p2_/Pa_]],p1_/Pa_*(V1_/m_^3/V_),[[V4_/m_^3,p4_/Pa_],[V5_/m_^3,p5_/Pa_]],[[.9*V2_/m_^3,p3_/Pa_],[V3_/m_^3,p3_/Pa_]],p2_/Pa_*(V2_/m_^3/V_)^subs(dat,gamma)},V_=.9*V2_/m_^3..1.1*V3_/m_^3,pre=0.9*p3_/Pa_..1.1*p2_/Pa_

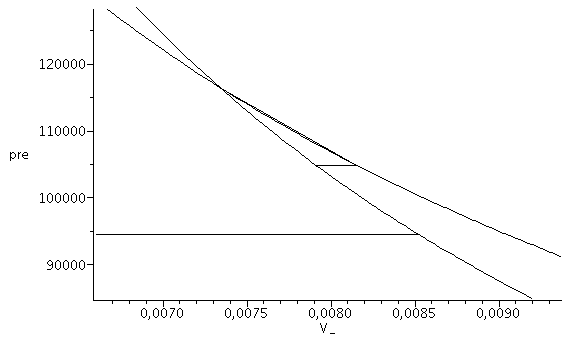>	,colour=black);

e) Diagrama T-s de la evolución.

Variaciones de entropía del gas:

>

eqDS:=DS12='m*(c[p]*ln(T2/T1)-R*ln(p2/p1))';DS12_:=subs(dat,m*(c[p]*ln(T2/T1)-R*ln(p2_/p1_))):DS12=evalf(%,3);DS24_:=subs(dat,dat,evalf(subs(dat,m*(c[p]*ln(T4_/T2)-R*ln(p4_/p2_))))):DS24=evalf(%,3);DS45_:=subs(dat,dat,evalf(subs(dat,m*(c[p]*ln(T5_/T4_)-R*ln(p5_/p4_))))):DS45=evalf(%,3);S0:=0.5*J_/K_:plot(subs(dat,SI0,{[S0+m*(c[p]*ln(T/T0)),T,T=270..300],[[S0,T0],[S0+DS12_,T2],[S0+DS12_,T3_]]}),S=0..1,T=250..300);

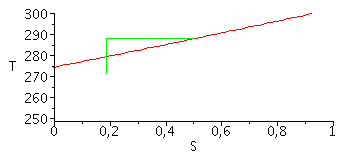f) Variación de entropía y generación de entropía para todos los sistemas entre los estados antedichos y para todo el ciclo..

De 1 a 2 hay un flujo de entropía isotermo con el ambiente, así que, despreciando la fricción, no habrá generación de entropía.

>	DS12amb:=Q12amb/Tamb;DS12amb_:=subs(dat,-Q12_/T0):'DS12amb'=evalf(%,3);Sgen:='DS+DSamb';Sgen12_:=DS12_+DS12amb_:'Sgen12'=evalf(%,2);Sgen12:=0;

ya que era la incertidumbre del redondeo.

De 2 a 4 se ha supuesto isoentrópica la evolución del gas, pero sí hay generación de entropía for fricción entre el émbolo y el cilindro, que se podrá aproximar suponiendo que esa disipación pasa al ambiente. La disipación viscosa a ambos lados del émbolo puede despreciarse.

>	DS24_:=subs(dat,dat,evalf(subs(dat,m*(c[p]*ln(T4_/T2)-R*ln(p4_/p2_))))):DS24=evalf(%,3);DS24:=0;DS24amb:=Q24amb/Tamb;DS24amb:=-W24/Tamb;DS24amb_:=subs(dat,-W24_/T0):'DS24amb'=evalf(%,3);Sgen24_:=DS24_+DS24amb_:'Sgen24'=evalf(%,3);

De 4 a 5 hay un flujo isobárico de entropía.

>	DS45amb:=Q45amb/Tamb;DS45amb_:=subs(dat,-Q45_/T0):'DS45amb'=evalf(%,3);Sgen45_:=DS45_+DS45amb_:'Sgen45'=evalf(%,2);

y para el ciclo completo:

>	DS15:='DS12+DS24+DS45';DS15_:=DS12_+DS24_+DS45_:'DS15'=evalf(%,3);DS15:=0;DS15amb:='DS12amb+DS24amb+DS45amb';DS15amb_:=DS12amb_+DS24amb_+DS45amb_:'DS15amb'=evalf(%,3);Sgen15:='Sgen12+Sgen24+Sgen45';Sgen15_:=Sgen12_+Sgen24_+Sgen45_:'Sgen15'=evalf(%,3);

>