>	restart:#"m02_p13"

En un cilindro horizontal abierto por un extremo, un mbolo de latn de 15 cm de diámetro y 3 cm de espesor, encierra 0,5 mol de argn inicialmente en equilibrio con el ambiente. A partir de un cierto instante, se ancla el mbolo y se eleva 15 C la temperatura mediante una fuente de calor, y despus se retira la fuente y se deja libre el mbolo. Se pide:
a) Determinar la posicin del mbolo, la presin tras el calentamiento, y el calor recibido por el argn
b) Diagramas esquemáticos p-V y T-s de la evolucin prevista del argn. Indicar la bondad de establecer un modelo matemático lineal de los procesos.
c) Energa cintica máxima alcanzada por el mbolo.

d) Presin, posicin del mbolo y temperatura en los estados de equilibrio mecánico y termodinámico.
e) Posiciones extremas del mbolo en su movimiento.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):

>	su1:="Ar":su2:="Laton":dat:=[D=0.15*m_,LE=0.03*m_,n=0.5*mol_,DT=15*K_]:dat:=[op(dat),evalf(subs(dat,A=Pi*D^2/4))]:evalf(%,2);

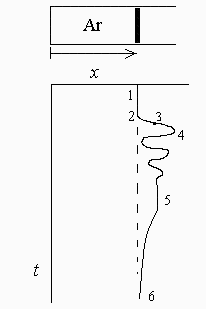
Esquema:

>

>

Ecs. const.:

>	eqET:=subs(eq1_11,eq1_12);eqEE:=eq1_16;gdat:=get_gas_data(su1):sdat:=get_sol_data(su2):dat:=op(dat),Const,gdat,SI2,SI1:

a) Determinar la posicin del mbolo, la presin tras el calentamiento, y el calor recibido por el argn.

>	eqET:=x1=n*R[u]*T1/(p1*A);x1_:=subs(T1=T0,p1=p0,dat,rhs(eqET));eq12:=V=cte;eq12:=p1/T1=p2/T2;p1_:=subs(dat,p0);T1_:=subs(dat,T0);T2_:=subs(dat,T0+DT);p2_:=subs(dat,p0*(T0+DT)/T0):'p2'=evalf(%,3);x2:='x1';eqBE:=DE=Q+W;eqBE:=Q=n*M*c[v]*DT;eqBE_:=subs(dat,eqBE):evalf(subs(Q=Q12,%));

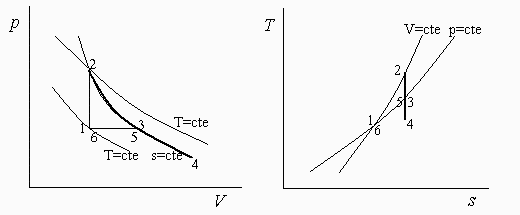
b) Diagramas esquemáticos p-V y T-s de la evolucin prevista del argn. Indicar la bondad de establecer un modelo matemático lineal de los procesos.

El forzamiento es un DT<<T0 (15/288) y por tanto la aproximacin lineal será muy buena. Tomando incrementos respecto al estado inicial:

>	eqET12lin:=Dp/p0=DT/T0;Dp12_:=subs(dat,p0*DT/T0);

Ntese que es mejor trabajar con los incrementos que con las funciones para evitar inconsistencias en el tratamiento de las incertidumbres.

c) Energa cintica máxima alcanzada por el mbolo.

La energa cintica máxima será cuando la velocidad sea máxima y por tanto la aceleracin nula, luego será p3=p0, despreciando la friccin.

>

eqBFemb:=mE*Diff(x,t,t)=(p-p0)*A+Ff;eqBEemb23:='mE*v3^2/2=Int((p-p0)*A,x=x2..x3)+Int(Ff,x=x2..x3)';eq2:=mE=rho*A*LE;mE_:=subs(sdat,dat,rhs(eq2)):'mE'=evalf(%,2);eq23:=pV^gamma=cte;p3:=p0;eq23:=x3=x2*(p2/p3)^(1/gamma);eq23_:=subs(x1=x1_,p2=p2_,dat,eq23):evalf(%,2);eqBEemb23_:=subs(p=p2*(x2/x)^gamma,eqBEemb23);eqBEemb23__:=subs(dat,evalf(subs(eq23_,p2=p2_,x1=x1_,Ff=0,dat,value(eqBEemb23_)))):evalf(%,2);

>

eq23lin:=p/p2=(x2/x)^gamma;eq23lin:=(p0+Dp)/(p0+Dp12)=(x1/(x1+Dx))^gamma;eq23lin:=(Dp-Dp12)/p0=-gamma*Dx/x1;Dx23_:=subs(dat,x1_*Dp12_/(gamma*p0)):'Dx23'=evalf(%,2);eqBEemb23lin:=lhs(eqBEemb23)=Int(Dp*A,Dx=0..Dx23);eqBEemb23lin_:=lhs(eqBEemb23)=int((Dp12-p0*gamma*Dx/x1)*A,Dx=0..Dx23);eqBEemb23lin__:=subs(Dp12=Dp12_,x1=x1_,Dx23=Dx23_,dat,eqBEemb23lin_):'Ec_max'=evalf(rhs(%),2);

d) Presin, posicin del mbolo y temperatura en los estados de equilibrio mecánico y termodinámico.

>	eq25:=pV^gamma=cte;p5:=p0;T5:='T2*(p5/p2)^((gamma-1)/gamma)';T5_:=subs(T2=T2_,p2=p2_,dat,T5);x5:='n*R[u]*T5/(p5*A)';x5_:=subs(T2=T2_,p2=p2_,dat,x5);p6:='p1';T6:='T1';x6:='x1';

e) Posiciones extremas del mbolo en su movimiento.

>

eq24:=p*V^gamma=cte;eq24:=p4*(A*x4)^gamma=p2*(A*x2)^gamma;eq24_:=subs(x1=x1_,p2=p2_,dat,SI0,eq24):'eq24'=evalf(%,2);eqBEemb24:=mE*g*(x4-x2)=Int((p-p0)*A,x=x2..x4);eqBE_:=subs(mE=mE_,x1=x1_,dat,SI0,value(subs(p=p2_*(x1_/x)^gamma,eqBEemb24))):'eqBE'=evalf(%,2);sol_:=fsolve({eq24_,eqBE_},{x4,p4},x4=.5..1.5);x4_:=subs(sol_,x4)*m_:'x4'=evalf(%,2);p4_:=subs(sol_,p4)*Pa_;T4_:=subs(dat,p4_*A*x4_/(n*R[u]));

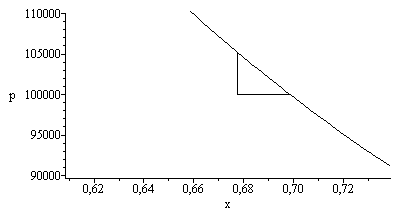
Representacin de la evolucin en el diagrama p-V (en realidad p-x).

>	pl12:=(subs(x1=x1_,dat,SI0,[[x1_,p1_],[x2,p2_]])):pl24:=(subs(x1=x1_,dat,SI0,p2_*(x2/x)^gamma),x=subs(x1=x1_,dat,SI0,x2)..subs(dat,SI0,x4_)):pl56:=(subs(x1=x1_,p1=p0,p2=p2_,T2=T2_,dat,SI0,[[x5,p5],[x6,p6]])):plot({pl12,pl24,pl56},x=0.9*x1_/m_..x4_/m_,'p'=0.9e5..1.1e5,colour=black);

Elijo un valor S=0 inicial.

>	S0:=0:S1:=S0:DS12:=n*M*c[v]*ln(T2_/T1_):DS23:=0:DS34:=0:DS45:=0:DS56:=n*M*c[p]*ln(T1_/T5_);plot(subs(dat,SI0,[[S0,T1_],[S0+DS12,T2_],[S0+DS12+DS23,T5_],[S0+DS12+DS23+DS34,T4_],[S0+DS12+DS23+DS34+DS45,T5_],[S0+DS12+DS23+DS34+DS45+DS56,T1_]]),'S'=0..0.35,T_K=250..310,colour=black);

>
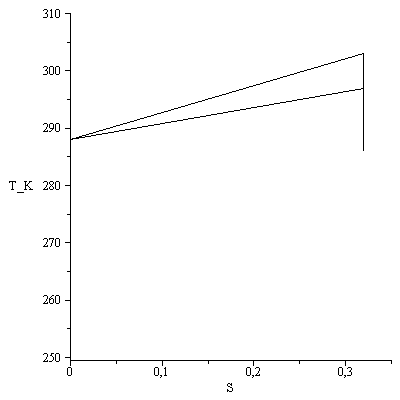