| > | restart:#"m02_p04" |
Sabiendo que para gases monoatómicos ideales en equilibrio, la energía cinética media del movimiento microscópico es Ec=(1/2)mv^2=(3/2)kT, se pide:
a) ¿Por qué no cesa ese movimiento relativo en el equilibrio termodinámico?
b) Determinar la distribución de máxima entropía de los módulos de las velocidades.
c) Determinar la distribución de máxima entropía de partículas según su velocidad.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots):assume(k>0,T>0,m>0,mu<0,v[max]>0,M>0,R>0,T>0);interface(displayprecision=4): |
| > | EqE:=[E[c,mean]=(3/2)*k*T];su:="Ar":dat:=get_gas_data(su),Const,SI2,SI1: |
a) ¿Por qué no cesa ese movimiento relativo en el equilibrio termodinámico?
Existe el movimiento microscópico molecular en el equilibrio porque el sistema está cargado de energía térmica que con el modelo de gas ideal monoatómico clásico sólo es energía cinética de traslación, que es directamente proporcional a la temperatura y solo depende de ella, luego, si se mantiene T=cte, se mantiene invariable el movimiento microscópico (movimiento térmico).
b) Determinar la distribución de máxima entropía de los módulos de las velocidades.
c) Determinar la distribución de máxima entropía de partículas según su velocidad.
Suponemos que las velocidades moleculares tienen módulo de cualquier valor, v (positivo y continuo) y en cualquier dirección (simetría esférica de los vectores velocidad en las coordenadas espaciales). Sea p(v)dv la probabilidad de que una partícula tenga un módulo de velocidad comprendido entre v y v+dv, y sea n(v)dv=p(v).4pv2dv)=máxima, sujeto a las condiciones de normalización Int(p.4pv2dv)=1 y de conservación de la energía Int(p(1/2)mv2.4pv2dv=E[c,mean].
| > | eqN:=Int(p(v)*4*Pi*v^2,v=0..infinity)=1;eqS:=Int(-k*p(v)*ln(p(v))*4*Pi*v^2,v=0..infinity)=S;eqE:=Int(p(v)*(1/2)*m*v^2*4*Pi*v^2,v=0..infinity)=E[c,mean]; |
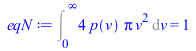 |
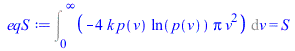 |
![Int(`+`(`*`(2, `*`(p(v), `*`(m, `*`(`^`(v, 4), `*`(Pi)))))), v = 0 .. infinity) = E[c, mean]](images/np04_4.gif) |
Este problema se resuelve por el método de los multiplicadores de Lagrange. Se construye la función de Lagrange, Phi, y se calcula su extremo no condicionado:
| > | Phi:=rhs(eqS+lambda*eqN+mu*eqE);Phi:=subs(p(v)=p,lhs(eqS+lambda*eqN+mu*eqE));DPhi:=diff(Phi,p)=0;DPhi_:=diff(subs(infinity=v,DPhi),v);p_:=solve(DPhi_,p); |
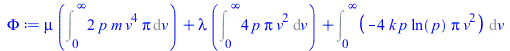 |
 |
Y después se determina el valor de los multiplicadores con las ecuaciones iniciales:
| > | eqN_:=subs(p(v)=p_,eqN);eqN_:=value(expand(eqN_));eqE_:=subs(p(v)=p_,eqE);eqE_:=value(expand(subs(EqE,eqE_)));sol1:=combine(allvalues(solve({eqN_,eqE_},{lambda,mu})));p__:=expand(subs(sol1,p_)):'p'=%;n:=expand(p__*4*Pi*v^2);Int('p',v=0..infinity)=simplify(int(p__,v=0..+infinity));Int('n',v=0..infinity)=simplify(int(n,v=0..+infinity)); |
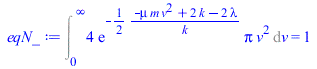 |
 |
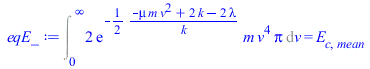 |
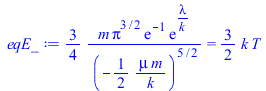 |
| Warning, solve may be ignoring assumptions on the input variables. |
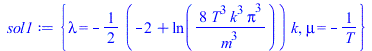 |
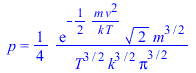 |
 |
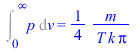 |
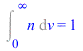 |
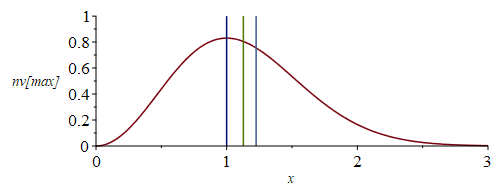
Conclusión, p es una probabilidad no normalizada, p(v^2) es una exponencial decreciente, p(v) es parecida pero con salida horizontal. Pero n si está normalizada, n(v) es creciente y luego decreciente como se apreciará en el gráfico abajo. Aunque no se ha deducido, la probabilidad que tiene una molécula de tener una componente de la velocidad (e.g. en la dirección x) vx es una distribución normal de Gauss.
Los momentos de la distribución son:
| > | intn:=simplify(int(n,v=0..infinity)):Int('n',v=0..infinity)=intn;intnv:=simplify(int(n*v,v=0..infinity)):Int('n*v',v=0..infinity)=intnv;intnvv:=simplify(int(n*v*v,v=0..infinity)):Int('n*v*v',v=0..infinity)=intnvv; |
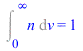 |
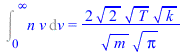 |
 |
Y los valores medios y el máximo:
| > | eqv_rms:=v[rms]=sqrt(Int('v^2*n',v=0..infinity)/Int('n',v=0..infinity));eqv_rms_:=v[rms]=sqrt(intnvv/intn);eqv_mean:=v[mean]=Int('v*n',v=0..infinity)/Int('n',v=0..infinity);eqv_mean_:=v[mean]=intnv/intn;eqv_max:=Diff('n',v)=0;eqDn0:=diff(n,v)=0:sol2:=solve({eqDn0},v):eqv_max_:=v[max]=subs(sol2[2],v); |
![v[rms] = `*`(`^`(`/`(`*`(Int(`*`(n, `*`(`^`(v, 2))), v = 0 .. infinity)), `*`(Int(n, v = 0 .. infinity))), `/`(1, 2)))](images/np04_22.gif) |
![v[mean] = `/`(`*`(Int(`*`(n, `*`(v)), v = 0 .. infinity)), `*`(Int(n, v = 0 .. infinity)))](images/np04_24.gif) |
![v[mean] = `+`(`/`(`*`(2, `*`(`^`(2, `/`(1, 2)), `*`(`^`(T, `/`(1, 2)), `*`(`^`(k, `/`(1, 2)))))), `*`(`^`(m, `/`(1, 2)), `*`(`^`(Pi, `/`(1, 2))))))](images/np04_25.gif) |
| Warning, solve may be ignoring assumptions on the input variables. |
Conviene trabajar con variables reducidas, i.e. von velocidades relativas a la máxima, o a la media, o a la rms, o a otra velocidad característica como vc=sqrt(kT/m). Aquí vamos a dividir por la vmax=sqrt(2kT/m).
| > | 'v[max]=sqrt(2*k*T/m)';eqx:=x='v/v[max]';'v[mean]/v[max]'=(simplify(subs(eqv_max_,eqv_rms_,eqv_mean_,v[mean]/v[max])));evalf(%);'v[rms]/v[max]'=simplify(subs(eqv_max_,eqv_rms_,eqv_mean_,v[rms]/v[max]));evalf(%); |
![`/`(`*`(v[mean]), `*`(v[max])) = `+`(`/`(`*`(2), `*`(`^`(Pi, `/`(1, 2)))))](images/np04_30.gif) |
Adimensionalizamos la distribución del número de partículas n(v):
| > | 'n'=n;'n'=simplify(subs(m=2*k*T/v[max]^2,n));eqx;nv[max]:=(4/sqrt(Pi))*x^2/exp(x^2);plot({[[1,0],[1,1]],[[1.128,0],[1.128,1]],[[1.225,0],[1.225,1]],nv[max]},x=0..3,'nv[max]'=0..1);Int_nv[max]:=simplify(int(nv[max],x=0..x));plot({[[1,0],[1,1]],[[1.128,0],[1.128,1]],[[1.225,0],[1.225,1]],[[0,0.5],[1.128,0.5]],Int_nv[max]},x=0..3,'Int_nv[max]'=0..1); |
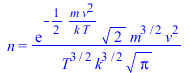 |
![n = `+`(`/`(`*`(4, `*`(exp(`+`(`-`(`/`(`*`(`^`(v, 2)), `*`(`^`(v[max], 2)))))), `*`(`^`(v, 2)))), `*`(`^`(Pi, `/`(1, 2)), `*`(`^`(v[max], 3)))))](images/np04_35.gif) |
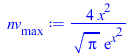 |
 |
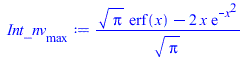 |
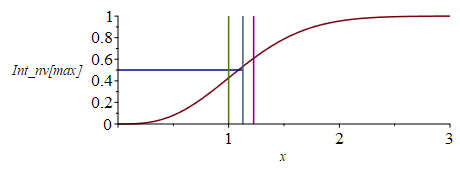 |
i.e. lo que es adimensional es la distribución del producto n(v)·v[max], y se ha dibujado su distribución y el valor acumulado. La p(v) es:
| > | 'p'=p__;'p'=simplify(subs(m=2*k*T/v[max]^2,p__));pv3[max]:=exp(-x^2)/Pi^(3/2);plot(pv3[max],x=0..3,'pv3[max]'=0..0.2); |
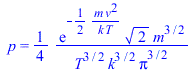 |
![p = `/`(`*`(exp(`+`(`-`(`/`(`*`(`^`(v, 2)), `*`(`^`(v[max], 2))))))), `*`(`^`(Pi, `/`(3, 2)), `*`(`^`(v[max], 3))))](images/np04_42.gif) |
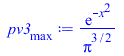 |
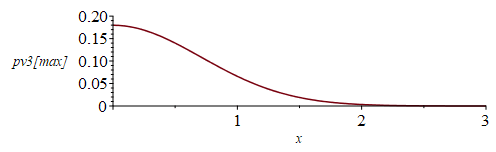 |
En resumen, el movimiento microscópico es con esa distribución de velocidades (y no todas las moléculas con igual velocidad v=v[sqr]) porque ésa es la distribución más probable, i.e. la de máxima entropía para la energía térmica dada.
Ejemplo para el argón a 15 ºC.
| > | eq0:=v[max]=sqrt(2*k*T/m);eq0:=v[max]=sqrt(2*R*T/M);R_:=subs(Const,R[u]);T_:=288*K_;M_:=subs(dat,M);eq0_:=v[max]=subs(dat,sqrt(2*R_*T_/M)):%;v[mean]=evalf(subs(k=R_,T=T_,m=M_,SI0,rhs(eqv_mean_)))*m_/s_;v[rms]=evalf(subs(k=R_,T=T_,m=M_,SI0,rhs(eqv_rms_)))*m_/s_;vmean_:=evalf(subs(k=R_,T=T_,m=M_,SI0,rhs(eqv_mean_))): |
i.e. si se tiene argón en equilibrio a 15 ºC, la probabilidad p(v)dv de que una molécula tenga un módulo de velocidad entre v y v+dv, es:
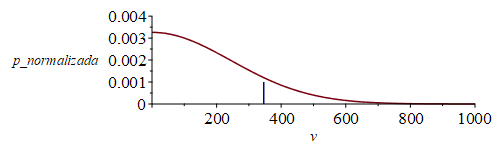
| > | 'pv3[max]'=pv3[max];'p_no_normalizada=pv3[max]/v[max]^3';p_normalizada:=2*Pi*subs(x=v/rhs(eq0),pv3[max])/rhs(eq0);p_normalizada:=evalf(subs(R=R_,T=T_,dat,SI0,%));plot({subs(SI0,[[rhs(eq0_),0],[rhs(eq0_),1e-3]]),%},v=0..1000,'p_normalizada'=0..0.004);Int('p_normalizada',v=0..v[max])=int(p_normalizada,v=0..subs(SI0,rhs(eq0_)));Int('p_normalizada',v=0..infinity)=int(p_normalizada,v=0..+infinity); |
![pv3[max] = `/`(`*`(exp(`+`(`-`(`*`(`^`(x, 2)))))), `*`(`^`(Pi, `/`(3, 2))))](images/np04_53.gif) |
![p_no_normalizada = `/`(`*`(pv3[max]), `*`(`^`(v[max], 3)))](images/np04_54.gif) |
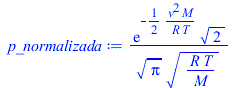 |
 |
![Int(p_normalizada, v = 0 .. v[max]) = .8427007928](images/np04_58.gif) |
 |
i.e. la p (normalizada o no) varía como una gaussiana, pero solo vale para v>0 porque son módulos. El módulo más probable es v=0, pero lo que interesa es la fracción de moléculas con módulo v entre v y v+dv, que es la n(v) y es:
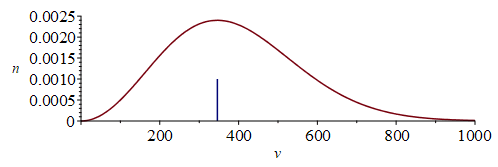
| > | 'nv[max]'=nv[max];n_:=subs(m=M,k=R,n);n__:=evalf(subs(R=R_,T=T_,M=M_,SI0,%));plot({subs(SI0,[[rhs(eq0_),0],[rhs(eq0_),1e-3]]),%},v=0..1000,'n'=0..0.0025);Int('n',v=0..v[max])=int(n__,v=0..subs(SI0,rhs(eq0_)));Int('n',v=0..v[mean])=int(n__,v=0..vmean_);Int('n',v=0..v[rms])=int(n__,v=0..subs(SI0,subs(k=R_,T=T_,m=M_,SI0,rhs(eqv_rms_))));Int('n',v=0..infinity)=int(n__,v=0..+infinity);n___:=subs(v=y,n__):vmedian:=fsolve(1/2=int(n___,y=0..y),y=300..500):v[median]:=%*m_/s_;Int('n',v=0..'v[median]')=int(n___,y=0..vmedian);eq_sigma:=sigma=sqrt(R*T/M)*sqrt(3-8/Pi);eq_sigma:=sigma=evalf(subs(SI0,sqrt(R_*T_/M_)*sqrt(3-8/Pi)))*m_/s_;eq_sigma_check:=sqrt(Int('n*(v-v[mean])',v=0..infinity))=sqrt(int(n___*(y-390.43)^2,y=0..+infinity))*m_/s_; |
![nv[max] = `+`(`/`(`*`(4, `*`(`^`(x, 2))), `*`(`^`(Pi, `/`(1, 2)), `*`(exp(`*`(`^`(x, 2)))))))](images/np04_60.gif) |
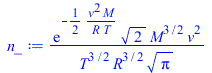 |
 |
![Int(n, v = 0 .. v[max]) = .4275932955](images/np04_64.gif) |
![Int(n, v = 0 .. v[mean]) = .5330502003](images/np04_65.gif) |
![Int(n, v = 0 .. v[rms]) = .6083748236](images/np04_66.gif) |
 |
![Int(n, v = 0 .. v[median]) = .5000000002](images/np04_69.gif) |
![`*`(`^`(Int(`*`(n, `*`(`+`(v, `-`(v[mean])))), v = 0 .. infinity), `/`(1, 2))) = `+`(`/`(`*`(164.7668793, `*`(m_)), `*`(s_)))](images/np04_72.gif) |
i.e. el número de átomos de argón con módulo de velocidad v<v[max]=346 m/s es del 43 % del total. Nótese que:
-v[max]=346 m/s es el módulo más frecuente, i.e. la moda, pero no la velocidad máxima, que es infinito en este modelo clásico.
-v[median]=376 m/s es el módulo que divide el total de átomos en dos mitades iguales: la mitad tiene v<376 m/s y la otra mitad tiene v>376 m/s.
-v[mean]=390 m/s es la media, tal que el primer momento a cada lado coincide.
-v[rms]=424 m/s es la media cuadrática, tal que el segundo momento a cada lado coincide.
-sigma=sqrt(RT/M)·sqrt(3-8/Pi)=165 m/s es la desviación estándar de la distribución de M-B.
-No tiene sentido preguntarse por qué fracción de átomos tienen una cierta velocidad (e.g. la v[max], o 500 m/s). Se trata de una distribución continua y la probabilidad de un punto es nula. Sí es calculable la fracción de átomos con v=376+/-1 m/s, o entre vmean-sigma y vmean+sigma:
| > | n_mol:=p*V/(R/T);p_:=1e5*Pa_;V_:=0.001*m_^3;n_mol_:=subs(dat,p_*V_/(R_*T_));n_atom:='n_mol*N[A]';n_atom_:=subs(dat,n_mol_*N[A]);'v[mean]'=vmean_*m_/s_; |
Entre vmean+1 m/s y vmean-1 m/s hay:
| > | eq_vmean_mm_1:=Int('n',v=v[mean]-1..v[mean]+1)=int(n___,y=vmean_-1..vmean_+1);;Delta*'n_mol'=rhs(eq_vmean_mm_1)*n_mol_;Delta*'n_atom'=rhs(eq_vmean_mm_1)*n_atom_; |
![Int(n, v = `+`(v[mean], `-`(1)) .. `+`(v[mean], 1)) = 0.4649176005e-2](images/np04_80.gif) |
i.e. para argón a 15 ºC, la fracción de átomos con v=390+/-1 m/s es del 0,46 % (en 1 L a 100 kPa, de los 40 mmol total, 0,02 mmol, o 1,2e20 átomos de los 2,5e22 totales).
Entre vmean+sigma y vmean-sigma hay:
| > | eq_vmean_mm_sigma:=Int('n',v=v[mean]-sigma..v[mean]+sigma)=int(n___,y=vmean_-rhs(eq_sigma)*s_/m_..vmean_+rhs(eq_sigma)*s_/m_);Delta*'n_mol'=rhs(eq_vmean_mm_sigma)*n_mol_;Delta*'n_atom'=rhs(eq_vmean_mm_sigma)*n_atom_; |
![Int(n, v = `+`(v[mean], `-`(sigma)) .. `+`(v[mean], sigma)) = .6761227949](images/np04_83.gif) |
i.e. para vmean+/-sigma, que para la distribución gaussiana sería el 68,2 % del total, para esta de M-B es casi igual, 67,6 % (en 1 L a 100 kPa, de los 40 mmol total, 28 mmol, o 1,7e22 átomos de los 2,5e22 totales).
| > |