>	restart:#"m01_p39"

En un recipiente esférico de vidrio de 10 cm de diámetro exterior, abierto al exterior por un tubo de vidrio de 10 mm de diámetro exterior y 20 cm de longitud, se vierten 10 cm3 de agua y, tapando con el dedo la boca del tubo, se le da la vuelta y se introduce la boca 1 cm por debajo del nivel del agua en un gran depósito, y se retira el dedo. Suponiendo que todo el vidrio es de 1 mm de espesor uniforme, se pide:
a) Sea z la altura a la que ha quedado el menisco en el tubo, respecto al nivel del agua exterior, y V0 la capacidad del recipiente (supóngase medio litro). Deducir expresiones linealizadas para las variaciones de z con la presión y temperaturas atmosféricas. Calcular los valores numéricos de los coeficientes de sensibilidad anteriores.
b) Calcular la altura de equilibrio en condiciones estándar.
c)   Calcular la variación de temperatura que experimentará el aire encerrado al quitar el dedo.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):

>	su1:="Aire":su2:="H2O":dat:=[De=0.1*m_,de=0.01*m_,L=0.2*m_,Vl1=10e-6*m_^3,Lsub=0.01*m_,ev=1e-3*m_,V0=0.5e-3*m_^3]:A=Pi*(de-2*ev)^2/4;dat:=[op(dat),evalf(subs(dat,%))];

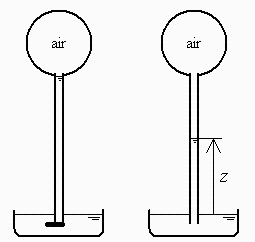
Esquema:

>

>

Ecs. const.:

>	eqET:=eq1_14;Adat:=get_gas_data(su1):Wdat:=get_liq_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Sea z la altura a la que ha quedado el menisco en el tubo, respecto al nivel del agua exterior, y V0 la capacidad del recipiente (supóngase medio litro). Deducir expresiones linealizadas para las variaciones de z con la presión y temperaturas atmosféricas. Calcular los valores numéricos de los coeficientes de sensibilidad anteriores.

Considerando como sistema el aire atrapado, y llamando p0 y T0 a lo valores stándar:atmosféricos:

>	eqETlin:=Dp/p0+DV/V0=DT/T0;eqBF:=p=patm-rho*g*z;eqBF:=Dp=Dpatm-rho*g*Dz;eqV:=DV=-A*Dz;eqT:=DT=DTatm;eqETlin_:=subs(eqBF,eqV,eqT,eqETlin);eq_p_sen:=(Dz/Dpatm)[T]=subs(DTatm=0,solve(eqETlin_,Dz)/Dpatm);subs(Wdat,dat,%);eq_T_sen:=(Dz/Tpatm)[p]=subs(Dpatm=0,solve(eqETlin_,Dz)/DTatm);subs(Wdat,dat,%);

e.g. para una disminución típica de 1 kPa al pasar de buen tiempo a mal tiempo, el menisco bajaría 50 mm, pero para una variación típica de 10 ºC, el menisco intentaría moverse 175 mm y se saldría del tubo, rompiendo el sello hidráulico (escapándose burbujas) si se calienta o empezando a llenar la parte esférica, si se enfría.

b) Calcular la altura de equilibrio en condiciones estándar.

La presión en la boca ha de ser la misma que un poco más afuera a esa misma profundidad de 1 cm (no cae toda el agua porque aparece una depresión en el aire encerrado).

Sea z ahora la altura del nivel interior del agua desde la boca (no desde el nivel exterior).

>

eqBF:=rho*g*Lsub+p0=rho*g*z2+p2;eqBM:=p1*V1=p2*V2;eq0:=p1=p0;eq1:=V2=Vtot-z2*Pi*(de-2*ev)^2/4;eqVtot:=Vtot=Vesf+Vtub;Vesf:=Pi*(De-2*ev)^3/6;Vesf_:=evalf(subs(dat,%))*1e6*cm_^3/m_^3;Vtub:=L*Pi*(de-2*ev)^2/4;Vtub_:=evalf(subs(dat,%))*1e6*cm_^3/m_^3;subs(Vesf=Vesf_,Vtub=Vtub_,eqVtot);V1:=Vtot-Vl1;V1_:=evalf(subs(eqVtot,dat,%))*1e6*cm_^3/m_^3;sol_:=fsolve(subs(Wdat,eq0,eq1,eqVtot,dat,SI0,{eqBF,eqBM}),{z2,p2}):z2_:=subs(sol_,z2)*m_;p2_:=subs(sol_,p2)*Pa_;

Linealizando es más sencillo:

>	eqBF:=rho*g*Lsub+p0=rho*g*z2+p0+Dp2;eqBMlin:=Dp/p0+DV/Vtot=0;eqBMlin:=Dp2/p0+(Vl1-z2*A)/Vtot;sol_lin:=collect(solve({eqBF,eqBMlin},{z2,Dp2}),p0);sol_lin_:=subs(dat,evalf(subs(Wdat,eqVtot,dat,sol_lin)));

i.e. al darle la vuelta al recipiente, el nivel del agua se queda prácticamente justo en la unión del tubo y la esfera (caben 10.1 cm3 y hay 10 cm3), y al quitar el dedo de la boca, sale agua hasta que el nivel baja de los 20 cm iniciales a los 10,5 cm finales, produciéndose una depresión en al aire encerrado de casi 1 kPa.

c) Calcular la variación de temperatura que experimentará el aire encerrado al quitar el dedo.

La salida del agua es rápida y por tanto puede suponerse una expansión isoentrópica para el aire encerrado.Despreciando el posible efecto de la pequeña oscilación del nivel tras la suelta:

>	eqS:=p*V^gamma=cte;eqS:=T/p^((gamma-1)/gamma)=cte;eqSlin:=dT/T0-((gamma-1)/gamma)*dp/p0=0;DT:=T0*((gamma-1)/gamma)*Dp2/p0;DT_:=evalf(subs(sol_lin_,Adat,dat,DT),2);

i.e. el aire se enfriaría unos 0,8 ºC (y luego se atemperaría, descendiendo el nivel del menisco más lentamente otro poco.

>	Dz_:=-DT*(Dz/Tpatm)[p];Dz__:=evalf(subs(sol_lin_,eq_T_sen,Wdat,Adat,dat,%),2);

¡Vaya! como al final ha de bajar casi 10 cm, resulta que bajará 9 cm rápidamente y luego seguirá bajando todavía más de otro centímetro lentamente (a medida que le llegue calor del ambiente).

También se podría calcular la fuerza con que hay que mantener el recipiente y compararla con el peso del vidrio vacío, pero éste no es un problema térmico.

>