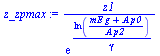>	restart:interface(warnlevel=0):#"m01_p08"

En un cilindro vertical de 5 cm de diámetro, abierto por arriba, un émbolo de 10 kg encierra una masa de 0,2 gramos de una mezcla gaseosa reactiva, que en un cierto instante se hace reaccionar, desprendiéndose 200 J en un intervalo de tiempo muy pequeño. Suponiendo que se puede considerar en todo momento (antes y después de reaccionar) que las propiedades medias de la mezcla gaseosa son cv=717 J.kg 1.K 1 y M=0,029 kg/mol, se pide:

a) Altura inicial del émbolo y presión inicial del gas.

b) Estado termodinámico que alcanzaría el gas encerrado inmediatamente después de la reacción (supuesto que no ha tenido tiempo de moverse).

c) Altura final que alcanzará el émbolo al cabo de mucho tiempo.

d) Altura máxima alcanzada por el émbolo y estado del gas en ese instante.

e) Altura alcanzada después de las oscilaciones, pero antes del equilibrado térmico, y estado del gas.

f) Velocidad máxima alcanzada por el émbolo.

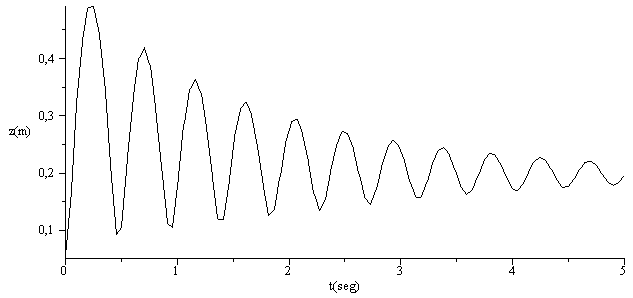
g) Integrar las ecuaciones del movimiento del émbolo y representar la posición en función del tiempo, suponiéndo que la fuerza de fricción es proporcional a la velocidad del émbolo, con un coeficiente de 10 N/(m/s).

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	dat:=[Di=0.05*m_,mE=10*kg_,m=0.2e-3*kg_,DUq=-200*J_,coe=10*N_/(m_/s_),c[v]=717*J_/(kg_*K_),M=0.029*kg_/mol_]:dat:=[op(dat),R=subs(Const,R[u])/subs(dat,M)]:dat:=[op(dat),gamma=subs(dat,(c[v]+R)/c[v]),A=evalf(subs(dat,(Pi*Di^2/4)))]:evalf(%,3);

Esquema:

>

>

Eqs. const.:

>	eqET:=subs(eq1_11,eq1_12);eqEE:=eq1_16-(DUq=0);dat:=[op(dat),Const,SI2,SI1]:

a) Altura inicial del émbolo y presión inicial del gas.

>	T1:=T0;p1:=p0+mE*g/A;p1_:=subs(dat,SI1,p1):p1__:=evalf(%/(1000*Pa_/kPa_));V1_:=solve(subs(p=p1,T=T1,dat,SI2,eqET),V):V1__:=evalf(%*(1e6*cm_^3/m_^3));z1_:=subs(dat,V1_/A):z1__:=evalf(%,2);dat:=[op(dat),'p1'=p1_,'z1'=z1_]:

b) Estado termodinámico que alcanzaría el gas encerrado inmediatamente después de la reacción (supuesto que no ha tenido tiempo de moverse).

>	eqBE:=eq1_5;eqBE:=subs(eqBE,subs(DE[m]=0,eq1_9));eqBE_:=subs(eqBE,W=0,Q=0,eqEE);T2_:=solve(subs(DT=T2-T1,dat,eqBE_),T2);p2_:=subs(SI0,dat,solve(subs(V=V1_,T=T2_,dat,Const,eqET),p))*Pa_:p2__:=evalf(%/(1000*Pa_/kPa_));dat:=[op(dat),'p2'=p2_,'z2'=z2_,'T2'=T2_]:

c) Altura final que alcanzará el émbolo al cabo de mucho tiempo.

>	T5:=T0;p5:=p0;z5:=z0;

d) Altura máxima alcanzada por el émbolo y estado del gas en ese instante.

>	deq1:=diff(z(t),t)=zp(t);deq2:=mE*diff(zp(t),t)=-mE*g+(p-p0)*A-coe*zp(t);ic1:=z(0)='z1';ic2:=zp(0)=0;

>	eqs:=subs(dat,SI0,{deq1,subs(p=p2*(z1/z(t))^gamma,deq2),ic1,ic2});

>	dsol1:=dsolve(eqs,{z(t),zp(t)},numeric):

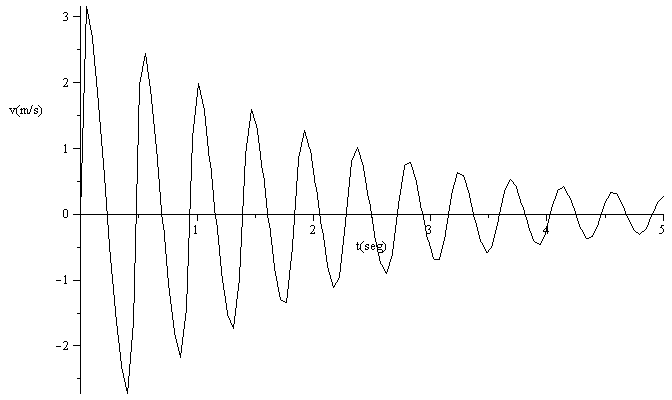
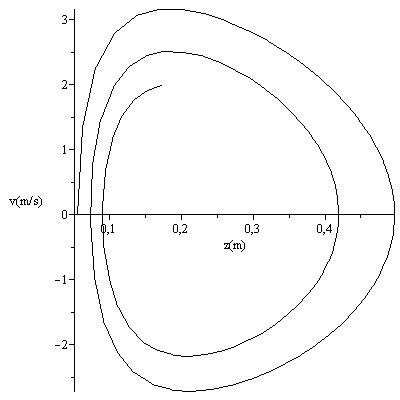
>	with(plots):odeplot(dsol1,[t,z(t)],0..5,numpoints=100,labels=["t(seg)","z(m)"],colour=black);odeplot(dsol1,[t,zp(t)],0..5,numpoints=100,labels=["t(seg)","v(m/s)"],colour=black);odeplot(dsol1,[z(t),zp(t)],0..1,numpoints=100,labels=["z(m)","v(m/s)"],colour=black);

>	eq1:=m*c[v]*(T3-T2)+mE*g*(z3-z1)=-p0*A*(z3-z1);eq1_:=subs(dat,SI0,eq1);eq2:=subs(p=p3,V=A*z3,T=T3,eqET);eq2_:=subs(p=p3,V=A*z3,T=T3,dat,SI0,eq2);eq3:=p3*z3^gamma=p2*z1^gamma;eq3_:=subs(dat,SI0,eq3);sol1:=fsolve({eq1_,eq2_,eq3_},{z3,p3,T3},z3=0..1):assign(sol1);

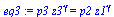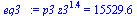>	z3_=evalf(z3,3)*m_;T3_=evalf(T3)*K_;p3_=evalf(p3/(1e3*Pa_/kPa_))*Pa_;

e) Altura alcanzada después de las oscilaciones, pero antes del equilibrado térmico, y estado del gas.

>	p4:=p1;z4_:=evalf(fsolve(subs(dat,SI0,p4*z4^gamma=p2*z1^gamma),z4=0..1))*m_:'z4'=evalf(%,3);T4_:=subs(dat,SI0,T2*z1^(gamma-1)/z4_^(gamma-1))*K_;

f) Velocidad máxima alcanzada por el émbol

>	z_zpmax:=solve(subs(p=p2*(z1/z)^gamma,coe=0,0=rhs(deq2)),z);z_zpmax_:=evalf(subs(dat,SI0,z_zpmax)):z_zpmax:=evalf(z_zpmax_)*m_;

>	eq1:=m*c[v]*(T6-T2)+mE*g*(z6-z1)+(1/2)*mE*zp^2=-p0*A*(z6-z1);eq1_:=subs(dat,SI0,eq1);eq2:=subs(p=p6,V=A*z6,T=T6,eqET);eq2_:=subs(p=p6,V=A*z6,T=T6,dat,SI0,eq2);eq3:=p6*z6^gamma=p2*z1^gamma;eq3_:=subs(dat,SI0,eq3);sol1:=fsolve(subs(z6=z_zpmax_,{eq1_,eq2_,eq3_}),{zp,p6,T6},zp=0..10):assign(sol1):

>	p6_:=evalf(p6/1000)*kPa_;T6_:=evalf(T6)*K_;zp_:=evalf(zp)*m_/s_;

el máximo de velocidad ocurre para t=0,06 s y el de altura para t=0,25

>