SI units |
The name Système International d’Unités (SI Units, in short) was adopted at the 11th General Assembly on Weights and Measures in 1960 (11th CGPM, Conférence Générale des Poids et Mesures), but, in spite of its name, it is not in common use in some places and instances, notably in the USA industry.
Physical sciences are based on measurable magnitudes, i.e. magnitudes that admit unambiguous size-comparison between those of the same class. Metrology is the science of measurement. Perhaps the crucial milestone in metrology took place in 1799, under the French Revolution, when scientists proposed to unify all different weights and measures into the decimal metric system.
A physical magnitude needs to be specified by three items: a unit of that dimension, a number indicating the ratio between the magnitude and the unit used, and a quantification of the accuracy or uncertainty in the previous number (measuring uncertainties can be reduced but never eliminated). It is common practice to implicitly include the uncertainty information in the number by limiting its number of significant figures accordingly, reducing the three parameters above to just two: the number and the unity, what might be further reduced to one if the unit were unambiguously understood (not several different units for the same magnitude, not multiples and submultiples).
Types of magnitude are length, time, volume, mass, temperature, etc. Quoting e.g. L=2.5 m refers to a magnitude L two-and-a-half times the length of the unit metre (m). Notice that the decimal sign is a point (.) in English language but a comma (,) for non-English texts; in any case, if there is no significant figure to the left of the decimal point, a zero must always be placed there (e.g. 0.3 and not .3).
Under the SI Units system, seven magnitudes are chosen to form a basic set (metre, kilogramme, second, ampere, kelvin, mole and candela), and all the others (e.g. hertz, newton, volt, radian) are regarded as being derived from this set by appropriate definitions involving only multiplication, division, differentiation or integration (thus, arguments of functions such as sin(x) or log(x) must be nondimensional; e.g. sin(wt), log(p/p0)).
The units quoted below are the basic units of
the Système International d’Unités.
NOTE: see 2019 redefinition of the SI base units (Wiki),
and non-SI units mentioned there (Wiki).
Length: The unit of length called the metre is the length of the path travelled by light in vacuum during a time interval of 1/299 792 458 of a second (17th CGPM, 1983).
Mass: The unit of mass called the kilogramme is the mass of the international prototype which is in the custody of the Bureau International des Poids et Mesures (BIPM) at Sévres, near Paris, France (3rd CGPM, 1901).
Time: The unit of time called the second is the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom (13th CGPM, 1967).
Temperature: The unit of temperature called the kelvin is the fraction 1/273.16 of the temperature of the triple point of water (13th CGPM, 1967).
Electric current: The unit of electric current called the ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 metre apart in a vacuum, would produce a force equal to 2´10-7 newton per metre of length between these conductors (9th CGPM, 1948).
Luminous intensity: The unit of luminous intensity called the candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540´1012 hertz and that has a radiant intensity in that direction of (1/683) watt per steradian (16th CGPM, 1970).
Amount of substance: The mole is the amount of substance of a system which contains as many elementary entities as there are atoms in 0.012 kilogramme of carbon 12 (14th CGPM, 1971). When the mole is used, the elementary entities must be specified and may be atoms, molecules, ions, electrons, other particles, or specified groups of such particles.
All derived units are products or ratios of basic units without numeric factors, most of them are dimensional (but radian, steradian and others are nondimensional) and some have special names (radian, steradian, hertz, newton, pascal, joule, watt, coulomb, volt, farad, ohm, siemens, weber, tesla, henry, degree Celsius, lumen and lux).
All basic units and derived units with special names have special symbols (m, kg, s, A, K, mol, cd, rad, sr, Hz, N, Pa, J, W, C, V, F, W, S, Wb, T, H, ºC, lm and lx).
Symbols for derived units are formed by appropriate combination of the special symbols above (e.g. m/s for velocity).
Instead of using raw numbers and base units (e.g. 6.380´106 m, 0.628´10-6 m, 0.012 V, 0.1´106 Pa), some multiples or submultiples of the base unit can be used in speech and writing (e.g. 6 380 km, 0.628 µm, 12 mV, 0.1 MPa), although care must be taken not to forget the factors during numerical calculations. In any case, be it as numerical exponents or as multiples of base units, it is recommended to use powers three order of magnitude apart, beginning on the base unit (e.g. 6.380´106 m and not 0.6380´107 m, 0.628´10-6 m and not 6.28´10-7 m). The prefix and value for the accepted multiples are:
Prefix
| Name | Symbol | Value |
| exa | E | 1018 |
| peta | P | 1015 |
| tera | T | 1012 |
| giga | G | 109 |
| mega | M | 106 |
| kilo | k | 103 |
| milli | m | 10-3 |
| micro | µ | 10-6 |
| nano | n | 10-9 |
| pico | p | 10-12 |
| fempto | f | 10-15 |
| atto | a | 10-18 |
Prefixes are applied to just one symbol-unit, and thus any exponent applies to the combination prefix-unit (e.g. 5 kN/m2=5´103 N/m2=0.5 N/cm2)
One exception to the use of prefixes occurs with the unit kilogramme, where the prefixes are applied to the unit gramme (e.g. 5 mg=5´10-6 kg).
Unit symbols must be written in normal upright characters without an end period (unless it is the end of the sentence), separated from the numeric quantity by one non-wrapable space, and remain unaltered in the plural (in writing, not in pronunciation).
Derived units which are products of base units must be
written with a period in between (e.g. N.m, or better N´m), those which are ratios can be written in one of the
three forms shown in the example for speed: m.s-1, m/s or
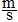 , although
the first one is preferable. These rules may be extended to more complex
grouping but more than one solidus (/) should never be used in the same
expression unless parentheses are used to avoid ambiguity.
, although
the first one is preferable. These rules may be extended to more complex
grouping but more than one solidus (/) should never be used in the same
expression unless parentheses are used to avoid ambiguity.
| magnitude |
symbol |
unit |
symbol |
equivalence |
| length |
l, L |
metre |
m |
|
| mass |
m |
kilogramme |
kg |
|
| time |
t |
second |
s |
|
| electric current |
i |
ampere |
A |
|
| temperature |
T |
kelvin |
K |
|
| luminous intensity |
I,Iv |
candela |
cd |
|
| amount of substance |
n |
mole |
mol |
|
| angle (plane) |
a,b,g,q,f |
radian |
rad |
|
| solid angle |
w,W |
steradian |
sr |
|
| frequency |
n,f |
hertz |
Hz |
s-1 |
| force |
F |
newton |
N |
kg.m.s-2 |
| pressure |
p |
pascal |
Pa |
N.m-2 |
| energy |
E |
joule |
J |
kg.m2.s-2 |
| power |
P |
watt |
W |
J.s-1 |
| electric charge |
q,Q |
coulomb |
C |
A.s |
| el. potential difference |
V,f |
volt |
V |
W.A-1 |
| electric capacitance |
C |
farad |
F |
A.s.V-1 |
| electric resistance |
R |
ohm |
W |
V.A-1 |
| electric conductance |
G |
siemens |
S |
W -1 |
| magnetic flux |
F |
weber |
Wb |
V.s |
| magnetic flux density |
B |
tesla |
T |
Wb.m-2 |
| inductance |
L,M |
henry |
H |
Wb.A-1 |
| degree Celsius |
t |
degree Celsius |
ºC |
a) |
| luminous flux |
F |
lumen |
lm |
cd.sr |
| illumination |
E,i |
lux |
lx |
lm.m-2 |
a) There are two possibilities: for single temperature values, t, the numerical equivalence is t ºC=(t+273.15) K, whereas for differences in temperature, t, the numerical equivalence is t ºC=t K. For this reason it is impossible to automatically replace degree Celsius by kelvin in a text.
Other names and symbols that are temporarily accepted, but do not belong to the SI units are:
| magnitude | symbol | unit | equivalence |
| volume | V | litre | 1 l=10-3 m3 |
| mass | m | gramme | 1 g=10-3 kg |
| mass | m | tonne | 1 t=103 kg |
| time | t | minute | 1 min=60 s |
| time | t | hour | 1 h=3 600 s |
| time | t | day | 1 d=86 400 s |
| angle | a,b,g,q,f | degree | 1 º=p /180 rad |
| angle | a,b,g,q,f | minute | 1 '=p /10 800 rad |
| angle | a,b,g,q,f | second | 1 ''=p /648 000 rad |
| energy | e | electronvolt | 1 eV=1.602´10-19 J |
| length | L | Astronomic unit | 1 AU=149.598´109 m |
| length | L | parsec | 1 pc=30.857´1015 m |
| mass | m | atomic mass unit | 1 u=1.661´10-27 kg |
Physical equations represent natural laws or define new magnitudes.
They must be written in terms of physical magnitudes, that is, by means of symbols that represent at the same time a unit and a number.
All numeric factors appearing in a physical equation must be nondimensional.
When physical equations have empirical coefficients with dimensions, they must be represented by physical constants (symbols, comprising the unit and the number, made explicit apart).
Symbols for physical magnitudes should preferably be formed by one latin or greek letter, sometimes with subindices and other modifiers and must be printed in italic characters (symbols for units must be printed in normal upright font). A period should not follow to a symbol except for grammatical rules. To help on reading numbers with many figures, a small space may be used to separate groups of three figures at either side of the decimal sign (but never used a comma or a point).
Some nondimensional physical magnitudes are traditionally represented by a two-letter symbol (e.g. Re, Nu) and care must be taken not to take it as a product of two one-letter symbols in physical equations (a small space should be used). Notice that Re is in italics if it refers to the variable called Reynolds number but in upright Re if it refers to the function named real part.
Subindices can be used to distinguish different physical magnitudes with the same letter (e.g. cp, cv) or to represent the same physical magnitude applied to different systems or different times (e.g. m1, m2, for the mass of gas, mH2O). As shown above, literal names and numbers used as subindices are printed upright, but if variables are used to represent them (e.g. mi) they must be printed in italic.
Numbers must be printed in upright characters using a point at the baseline as decimal sign (a comma in non-English texts). The multiplication sign for numbers is a cross (e.g. 6.02´1023) for English texts and a mid-point or a cross for non-English texts (e.g. 6,02× 1023 or 6.02´1023).
Coefficients and factors (e.g. thermal expansion coefficient, a , dV/V=a dT are used to name dimensional magnitudes that appear in physical equations that show proportional dependence of the form A =KB.
Parameters, ratios and numbers (e.g. thermal capacity ratio g =cp/cv, Reynolds number Re=VL/n ) are used to name nondimensional magnitudes.
Fractions (e.g. mole fraction, xi) are used to name nondimensional magnitudes that are lower than unity.
Constants (e.g. Boltzmann constant, k=R/NA) are used to name dimensional magnitudes that do not vary with experimental circumstances. A bad usage occurs in the so called "chemical equilibrium constant", which is dependent on temperature.
Concentrations (e.g. mass concentration of a component B, r B=mB/V) are used to name a dimensional magnitude in a mixture divided by the volume of the mixture.
Densities (e.g. charge density, r =dQ/dV) are used to name a dimensional magnitude in a sufficiently small system divided by the volume of that system..
Flux densities (e.g. thermal flux density,
 ) are used to name the dimensional magnitude obtained by
division of a flux magnitude (one that pierces a control surface) by the area of
the surface.
) are used to name the dimensional magnitude obtained by
division of a flux magnitude (one that pierces a control surface) by the area of
the surface.
The adjective "specific" (e.g. specific volume, v=V/m) refers to the original magnitude divided by the mass of the system.
The adjective "molar" (e.g. molar volume, v=V/n) refers to the original magnitude divided by the amount of substance in the system.
Miscellaneous units and conversion values
The units listed below are grouped in:
- Light and thermal radiation units.
| Non-SI units of length |
name |
symbol |
equivalence |
| 1 angstrom |
Å |
= 10-10 m | |
| 1 astronomical unit |
AU |
= 1.496´1011 m | |
| 1 foot international |
ft (or ') |
= 0.3048 m | |
| 1 inch |
in (or '') |
= 0.0254 m | |
| 1 light year |
ly |
= 9.4605´1015 m | |
| 1 micron |
µ |
= 10-6 m | |
| 1 mil | = 2.54´10-5 m | ||
| 1 geographical mile |
mi |
= 1.853 184´103 m | |
| 1 imperial mile |
mi |
= 1.609 344´103 m | |
| 1 imperial nautical mile |
mi |
= 1.853 184´103 m | |
| 1 international nautical mile |
mi |
= 1.852´103 m | |
| 1 sea mile |
mi |
= 1.8288´103 m | |
| 1 parsec |
pc |
= 3.085 72´1016 m | |
| 1 yard |
yd |
= 0.9144 m | |
| Non-SI units of area | |||
| 1 square foot |
ft2 |
= 0.092 903 m2 | |
| 1 square inch |
in2 |
= 6.4516´10-4 m2 | |
| Non-SI units of volume | |||
| 1 cubic foot |
ft3 |
= 0.028 316 8 m3 | |
| 1 cubic inch |
in3 |
= 1.638 71´10-5 m3 | |
| 1 imperial gallon , UK |
gal |
= 4.546 091´10-3 m3 | |
| 1 dry gallon USA |
gal |
= 4.404 883 77´10-3 m3 | |
| 1 liquid gallon USA |
gal |
= 3.785 411´10-3 m3 | |
| 1 litre, liter |
l (or L) |
= 1.0´10-3 m3 | |
| Non-SI units of angle (plane) | |||
| 1 degree |
º |
= 0.017 453 3 rad | |
| 1 minute |
' |
= 2.908 88´10-4 rad | |
| 1 second |
'' |
= 4.848 14´10-6 rad | |
| Non-SI units of solid angle | |||
| 1 hemisphere | = 6.283 185 3 sr | ||
| Non-SI units of time | |||
| 1 day solar mean |
d |
= 8.6400´104 s | |
| 1 day sideral |
d |
= 8.6164´104 s | |
| 1 minute solar mean |
min |
= 60 s | |
| 1 second sidereal |
s |
= 0.997 269 56 s | |
| 1 year solar mean, tropical |
yr |
= 3.155 692 6´107 s | |
| 1 year sidereal |
yr |
= 3.155 815´107 s | |
| 1 year calendar (365 mean solar days) |
yr |
= 3.1536´107 s | |
| Non-SI units of velocity (linear) | |||
| 1 foot per second |
ft.s-1 |
= 0.3048 m.s-1 | |
| 1 inch per second |
in.s-1 |
= 0.0254 m.s-1 | |
| 1 kilometre per hour |
km.h-1 (or km/h) |
= 0.277 778 m.s-1 | |
| 1 knot international |
kn |
= 0.514 444 m.s-1 | |
| 1 knot UK |
kn |
= 0.514 773 m.s-1 | |
| 1 mile per hour |
mi.h-1 or (mph) |
= 0.447 04 m.s-1 | |
| Non-SI units of velocity (angular) | |||
| 1 cycle per second |
rev.s-1 |
= 6.283 185 rad.s-1 | |
| 1 hertz |
(Hz) |
= 6.283 185 rad.s-1 | |
| 1 revolution per minute |
rev.min-1 (or rpm) |
= 0.104 720 rad.s-1 | |
| Non-SI units of frequency | |||
| 1 radian per second |
rad.s-1 |
= 0.159 155 Hz | |
| 1 revolution per minute |
rev.min-1 (or rpm) |
= 0.016 667 Hz | |
| Non-SI units of acceleration | |||
| 1 foot per square second |
ft.s-2 |
= 0.304 800 m.s-2 | |
| 1 gravity, free fall standard |
g |
= 9.806 650 m.s-2 | |
| 1 Galileo |
Gal |
= 0.010 m.s-2 | |
| 1 inch per square second |
in.s-2 |
= 0.025 400 m.s-2 | |
| Non-SI units of mass | |||
| 1 atomic mass unit |
u |
= 1.661´10-27 kg | |
| 1 pound |
lb (or lbm) |
= 0.453 592 kg | |
| 1 slug | = 14.593 881 kg | ||
| 1 long ton, UK |
ton |
= 1.016 046´103 kg | |
| 1 metric tonne |
t |
= 1.0´103 kg | |
| Non-SI units of force | |||
| 1 dyne |
dyn |
= 1.0´10-5 N | |
| 1 kilogramme-force or kilopond |
kgf (or kp) |
= 9.806 N | |
| 1 pound-force |
lbf |
= 4.448 22 N | |
| Non-SI units of pressure | |||
| 1 atmosphere |
atm |
= 1.013 25´105 Pa | |
| 1 bar |
bar |
= 105 Pa | |
| 1 atmosphere technical |
at |
= 0.980 665´105 Pa | |
| 1 barye |
dyn.cm-2 |
= 0.1 Pa | |
| 1 inch of water at 4 ºC |
inH2O |
= 249.089 Pa | |
| 1 inch of mercury at 32 ºF |
inHg |
= 3.386 39´103 Pa | |
| 1 millibar |
mbar |
= 100.0 Pa | |
| 1 millimetre of mercury |
mmHg |
= 133.322 Pa | |
| 1 millimetre of water |
mmH2O |
= 9.806 65 Pa | |
| 1 pound-force per square inch |
psi |
= 6.894 76´103 Pa | |
| 1 torricelli |
tor |
= 133.322 Pa | |
| Non-SI units of viscosity (dynamic) | |||
| 1 centipoise |
cP |
= 10-3 Pa.s | |
| Non-SI units of viscosity (kinematic) | |||
| 1 centistokes |
cSt |
= 100 m2.s-1 | |
| Non-SI units of surface tensión | |||
| 1 dyne per centimetre |
dyn.cm-1 |
= 10-3 N.m-1 | |
| Non-SI units of energy, heat and work | |||
| 1 British thermal unit international |
Btu |
= 1.055 75´103 J | |
| 1 calorie thermal international |
calIT |
= 4.1868 J | |
| 1 kilocalorie |
kcal |
= 4.1868´103 J | |
| 1 gross calorie |
Cal |
= 4.1868´103 J | |
| 1 electronvolt |
eV |
= 1.602 1917´10-19 J | |
| 1 erg |
erg |
= 1.0´10-7 J | |
| 1 frigorie |
fr |
= -4.1855´103 J | |
| 1 therm | = 1.055´108 J | ||
| 1 thermie |
th |
= 4.1868´106 J | |
| 1 ton of refrigeration, US |
ton |
= 3.038 318´108 J | |
| Non-SI units of power | |||
| 1 British thermal unit per hour |
Btu/h |
= 0.293071 W | |
| 1 horsepower electric |
hp |
= 746.00 W | |
| 1 horsepower imperial |
hp |
= 745.70 W | |
| 1 horsepower metric |
hp |
= 735.499 W | |
| 1 horsepower water |
hp |
= 746.043 W | |
| 1 kilocalorie per hour |
kcal/h |
= 1.1630 W | |
| 1 ton of refrigeration per day, US |
ton |
= 3.516 85´103 W | |
| Non-SI units of specific energy | |||
| 1 British thermal unit per pound |
Btu/lb |
= 2.326´103 J.kg-1 | |
| 1 calorie (I.T.) per gramme |
calIT/g |
= 4.1868´103 J.kg-1 | |
| 1 kilocalorie (I.T.) per kilogramme |
kcalIT/kg |
= 4.1868´103 J.kg-1 | |
| Non-SI units of heat flux density | |||
| 1 British thermal unit per square foot hour |
Btu.ft-2.h-1 |
= 3.15459 W.m-2 | |
| 1 kilocalorie (I.T.) per square metre hour |
kcalIT.m-2.h-1 |
= 1.163 W.m-2 | |
| Non-SI units of temperature | |||
| t degree Celsius |
ºC |
= t + 273.15 K | |
| t degree Fahrenheit |
ºF |
= 5t/9 + 459.67 K | |
| t degree Rankine |
ºR |
= 5t/9 K | |
| Non-SI units of specific heat capacity | |||
| 1 British thermal unit per pound degree Celsius |
Btu.lb-1.ºC-1 |
= 2.326´103 J.kg-1.K-1 | |
| 1 British thermal unit per pound degree Fahrenheit |
(Btu.lb-1.ºF-1) |
=4.1868´103 J.kg-1.K-1 | |
| 1 kilocalorie per kilogramme kelvin |
kcalIT.kg-1.K-1 |
= 4.1868´103 J.kg-1.K-1 | |
| Non-SI units of thermal conductivity | |||
| 1 British thermal unit per foot second degree Fahrenheit |
Btu.ft-1.s-1.ºF-1 |
=6.23064´103 W.m-1.K-1 | |
| 1 British thermal unit per inch hour degree Fahrenheit |
Btu.in-1.h-1.ºF-1 |
= 20.7688 W.m-1.K-1 | |
| 1 kilocalorie (I.T.) per metre hour degree Celsius |
kcal.m-1.h-1.ºC-1 |
= 1.1630 W.m-1.K-1 | |
| Non-SI units of thermal conductance | |||
| 1 British thermal unit per square foot hour degree Fahrenheit |
Btu.ft-2.h-1.ºF-1 |
= 5.67826 W.m-2.K-1 | |
| 1 kilocalorie (I.T.) per square metre hour kelvin |
kcal.m-2.h-1.K-1 |
= 1.1630 W.m-2.K-1 | |
| Non-SI units of thermal diffusivity | |||
| 1 foot squared per hour |
ft2.h-1 |
= 2.58064´10-5 m2.s-1 | |
| 1 inch squared per hour |
in2.h-1 |
= 1.79211´10-7 m2.s-1 | |
| Non-SI units of luminance, brightness, illumination | |||
| 1 lux, lumen per square metre |
lx (or lm.m-2) |
= 0.159 155 cd.m-2 | |
| Non-SI units of luminous flux | |||
| 1 candle power spherical |
cd |
= 12.566 lm | |
| 1 watt of maximum visible radiation |
W |
= 683 lm | |
| 1 watt of solar radiation |
W |
= 96 lm | |
| 1 watt of 0.632 µm laser light |
W |
= 140 lm | |
| 1 watt of incandescent lamp at 300 K |
W |
= 15 lm | |
| Non-SI units of luminous intensity | |||
| 1 lumen of spherical luminous flux |
lm |
= 0.079 577 cd | |
| 1 lumen per steradian |
lm.sr-1 |
= 1 cd | |
| Non-SI units of illuminance, illumination | |||
| 1 candle per square meter |
cd.m-2 |
= 6.283 185 lx |
aThe above conversion applies to single temperature values, when dealing with differences in temperature, the relationship is 1 K = 1 ºC = 9/5 ºF = 9/5 ºR.
Fundamental physical constants
| Quantity |
Symbol |
Value |
Unit |
Uncertainty (ppm) |
| atomic mass unit |
mu |
1.660 565 5´10-27 |
kg |
5 |
| Avogadro constant |
NA |
6.022 045´1023 |
mol-1 |
5 |
| Boltzmann constant |
k |
1.380 662´10-23 |
J.K-1 |
8.5 |
| proton charge |
e |
1.602 189 2´10-19 |
C |
3 |
| curie |
Ci |
3.7´1010 |
disintegrations.s-1 |
exact |
| Einstein constant |
c2 |
8.987 551 79´1016 |
J.kg-1 |
exact |
| electron rest mass |
me |
9.109 534´10-31 |
kg |
0.6 |
| electronvolt |
eV |
1.602 189 2´10-19 |
J |
3 |
| electronic charge |
e |
1.602 189 2v10-19 |
C |
3 |
| Faraday constant |
F |
9.648 456´104 |
C.mol-1 |
3 |
| fine structure constant |
a |
7.297 350 6´10-3 |
- |
0.6 |
| first radiation constant |
c1 |
3.741 832´10-16 |
W.m2 |
0.6 |
| gas constant |
R |
8.314 41 |
J.mol-1.K-1 |
40 |
| gravitational acceleration |
g0 |
9.806 65 |
m.s-2 |
exact |
| universal gravitational constant |
G |
6.672´10-11 |
N.m2.kg-2 |
600 |
| ice-point temperature |
Tst |
273.15 |
K |
exact |
| Planck constant |
h |
6.626 076´10-34 |
J.s |
0.6 |
| proton rest mass |
mp |
1.672 648 5´10-27 |
kg |
0.6 |
| second radiation constant |
c2 |
0.014 387 86 |
m.K |
8.5 |
| speed of light in vacuum |
c |
2.997 924 58´108 |
m.s-1 |
exact |
| standard acceleration of free fall |
g0 |
9.806 65 |
m.s-2 |
exact |
| standard molar volume of ideal gas (at Tst and pst) |
Vst |
0.022 413 83 |
m3.mol-1 |
0.6 |
| standard pressure |
pst |
1.013 25´105 |
Pa |
exact |
| standard temperature |
Tst |
273.15 |
K |
exact |
| Stefan-Boltzmann constant |
s |
5.670 32´10-8 |
W.m-2.K-4 |
34 |
| triple point of water |
Ttr |
273.16 |
K |
exact |
| Wien’s radiation constant |
c3 |
2.897 790´10-3 |
m.K |
0.6 |