| > | restart:#"m18_p58" |
Se quiere estudiar la conveniencia de disponer una máquina de refrigeración con R134a que enfríe en verano la entrada de aire a una turbina de gas natural que aspira 50 m3/s de aire. La turbina tiene una relación de presiones de 20 y una temperatura máxima de 1500 K. Se piensa enfriar el aire de entrada desde 30 ºC hasta 10 ºC. Suponer rendimientos isoentrópicos del 85 % para compresores y turbina, y un salto mínimo de 5 ºC en los cambiadores de calor. Se pide:
a) Si no se pone la máquina de refrigeración, calcular el gasto másico de aire, el consumo de combustible, y la potencia neta, en verano (30 ºC).
b) Lo mismo, pero para entrada a 10 ºC.
c) Estados termodinámicos en el ciclo refrigerante.
d) Calor a extraer del aire en verano para que la entrada sea a 10 ºC, y gasto de refrigerante necesario.
e) Potencia necesaria para la máquina de refrigeración, y potencia neta de la instalación conjunta.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(RealDomain):interface(displayprecision=2): |
| > | su1:="CF3CH2F":su2:="Aire":dat:=[V=50*m_^3/s_,pi[12]=20,T3=1500*K_,T0=(30+273.15)*K_,T1=(10+273.15)*K_,eta=0.85,DT=5*K_,PCI=50e6*J_/kg_]; |
Tomamos PCI=50 MJ/kg para el gas natural, pues lo aproximamos a metano puro, CH4+2·O2=CO2+2·H2O, y PCI=2·242+394-75=802 kJ/mol=50 MJ/kg.
| > | dat:=op(dat),Const,SI2,SI1:Rdat:=get_gas_data(su1),get_liq_data(su1):pv:=get_pv_data(su1):Adat:=get_gas_data(su2): |
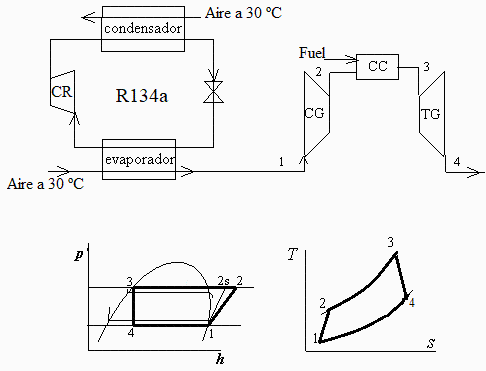
a) Si no se pone la máquina de refrigeración, calcular el gasto másico de aire, el consumo de combustible, y la potencia neta, en verano (30 ºC).
| > | T1_:=subs(dat,T0);p1_:=subs(dat,p0);ma=p1*V/(R*T1);ma_:=subs(Adat,dat,p0*V/(R*T1_));p2=p1*pi[12];p2_:=subs(dat,p0*pi[12]);eq5_59;eq5_61;T2_:=subs(eta[C]=eta,T1=T1_,p1=p1_,p2=p2_,Adat,dat,rhs(eq5_61));T3_:=subs(dat,T3);eqBEf:=mf*PCI=ma*c[p]*(T3-T2);mf_:=subs(Adat,dat,ma_*c[p]*(T3_-T2_)/PCI);eq5_60;eq5_62;p3=p2;p4=p0;T4_:=subs(eta[T]=eta,p4=p0,p3=p2_,Adat,dat,rhs(eq5_62));eqBE:=W=ma*c[p]*((T3-T4)-(T2-T1));eqBE_:=W=subs(Adat,dat,ma_*c[p]*((T3_-T4_)-(T2_-T1_)));eqeta:=eta=W/(mf*PCI);eqeta_:=eta=subs(eqBE_,dat,W/(mf_*PCI));ma30_:=ma_: |
![eta = `/`(`*`(`+`(`^`(pi[12], `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))), `*`(`+`(`/`(`*`(T2), `*`(T1)), `-`(1))))](images/p58_9.gif) |
![T2 = `*`(T1, `*`(`+`(1, `/`(`*`(`+`(`^`(`/`(`*`(p2), `*`(p1)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))), `*`(eta[C])))))](images/p58_10.gif) |
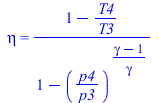 |
![T4 = `*`(T3, `*`(`+`(1, `-`(`*`(eta[T], `*`(`+`(1, `-`(`^`(`/`(`*`(p4), `*`(p3)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma)))))))))))](images/p58_16.gif) |
i.e. con entrada a 30 ºC, la turbina aspira 57,5 kg/s de aire, consume 0,83 kg/s de fuel, y da 14,5 MW de potencia con un rendimiento del 35 %.
b) Lo mismo pero para entrada a 10 ºC.
| > | T1_:=subs(dat,T1);p1_:=subs(dat,p0);ma=p1*V/(R*T1);ma_:=subs(Adat,dat,p0*V/(R*T1_));p2=p1*pi[12];p2_:=subs(dat,p0*pi[12]);eq5_61;T2_:=subs(eta[C]=eta,T1=T1_,p1=p1_,p2=p2_,Adat,dat,rhs(eq5_61));T3_:=subs(dat,T3);eqBEf:=mf*PCI=ma*c[p]*(T3-T2);mf_:=subs(Adat,dat,ma_*c[p]*(T3_-T2_)/PCI);eq5_60;p3=p2;p4=p0;eq5_62;T4_:=subs(eta[T]=eta,p4=p0,p3=p2_,Adat,dat,rhs(%));eqBE:=W=ma*c[p]*((T3-T4)-(T2-T1));eqBE_:=W=subs(Adat,dat,ma_*c[p]*((T3_-T4_)-(T2_-T1_)));eqeta:=eta=W/(mf*PCI);eqeta_:=eta=subs(eqBE_,dat,W/(mf_*PCI)); |
![T2 = `*`(T1, `*`(`+`(1, `/`(`*`(`+`(`^`(`/`(`*`(p2), `*`(p1)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))), `*`(eta[C])))))](images/p58_30.gif) |
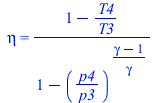 |
![T4 = `*`(T3, `*`(`+`(1, `-`(`*`(eta[T], `*`(`+`(1, `-`(`^`(`/`(`*`(p4), `*`(p3)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma)))))))))))](images/p58_38.gif) |
i.e., con entrada a 10 ºC, la turbina aspira 61,6 kg/s de aire, consume 0,95 kg/s de fuel, y da 17,5 MW de potencia con un rendimiento del 37 %. Vemos que en invierno la turbina funciona mejor, dando mayor potencia (17,5 MW frente a 14,5 MW), y con mayor rendimiento (37 % ahora frente a 35 % antes).
c) Estados termodinámicos en el ciclo refrigerante.
Para enfriar a 10 ºC debe vaporizarse a 5 ºC, y para evacuar el calor al ambiente a 30 ºC debe estar el condensar a 35 ºC.
| > | T1=T0-DT;T1_:=subs(dat,T1-DT);'T1_'=TKC(%);T3=T0+DT;T3_:=subs(dat,T0+DT);'T3_'=TKC(%);;p1=p[v](T1);p1_:=subs(dat,pv(T1_));p3_:=subs(dat,pv(T3_));p2_:=p3_;eq5_61;gamma=subs(Rdat,gamma);T2_:=subs(eta[C]=eta,T1=T1_,p1=p1_,p2=p2_,Rdat,dat,rhs(eq5_61));'T2_'=TKC(%);h1_:=subs(Rdat,T=T1_,dat,hv(T));h2_:=subs(Rdat,T=T2_,dat,hv(T));h3_:=subs(Rdat,T=T3_,dat,hl(T));h4_:=h3_;;h1l_:=subs(Rdat,T=T1_,dat,hl(T));x4=(h4-h1l)/(h1-h1l);x4_:=(h4_-h1l_)/(h1_-h1l_); |
![T2 = `*`(T1, `*`(`+`(1, `/`(`*`(`+`(`^`(`/`(`*`(p2), `*`(p1)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))), `*`(eta[C])))))](images/p58_54.gif) |
i.e. el compresor toma vapor saturado a 5 ºC y 353 kPa, lo comprime hasta 896 kPa y 36 ºC, sale del condensador como líquido saturado a 896 kPa y 35 ºC, pasa por la válvula al evaporador, donde entra a 353 kPa, 5 ºC, y con un 19 % de fracción másica de vapor.
d) Calor a extraer del aire en verano para que la entrada sea a 10 ºC, y gasto de refrigerante necesario.
La entrada a la turbina de gas será de 50 m3/s de aire a 10 ºC, i.e. 61,6 kg/s (de aire ambiente se aspirarán más: V·T0/T1=53,5 m3/s).
| > | 'ma'=ma_;eqQR:=QR=ma*c[p]*(T0-T1);QR_:=subs(ma=ma_,Adat,dat,rhs(eqQR));QR__:=subs(ma=ma30_,Adat,dat,rhs(eqQR)); |
i.e. para enfriar los 61,6 kg/s de aire desde 30 ºC a 10 ºC hay que quitarle 1,24 MW de calor (nótese que si se solo se aspiraran 50 m3/s a 30 ºC, 57,5 kg/s, habría que extraer solo 1,16 MW.
e) Potencia necesaria para la máquina de refrigeración, y potencia neta de la instalación conjunta..
| > | eqmR:=QR=mR*(h1-h4);mR_:=subs(dat,QR_/(h1_-h4_));eqWC:=WR=mR*(h2-h1);WR_:=subs(dat,mR_*(h2_-h1_));eqetaR:=eta[R]=QR/WR;eqetaR:=eta[R]=QR_/WR_;eqWnet:=Wnet=W_TG-W_CR;Wnet_:=rhs(eqBE_)-WR_; |
i.e. han de circular 7,65 kg/s de R134a para quitarle al aire los 1,24 MW antes calculados, lo que consume 0,2 MW en el compresor, así que la potencia neta se reduce de 17,5 MW a 17,3 MW, casi un 20 % mayor que sin la máquina de refrigeración (14,5 MW), aunque la pérdida de presión en los cambiadores, sobre todo en el evaporador con aire, disminuirán esta ventaja.
Más ventajoso sería usar una máquina refrigerante de absorción (e.g. de LiBr) que aprovechase el calor de los gases de escape de la turbina, en lugar de gastar potencia mecánica para mover el compresor de R134a. En Ibrahim et al (2011) se analizan otros sistemas de enfriamiento del aire de entrada a una turbina de gas.
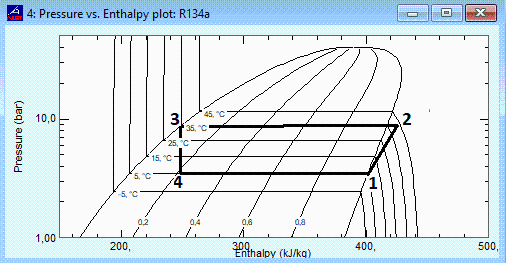
Para comparar este modelo de sustancia perfecta con datos más precisos, los valores del NIST para T1=5 ºC y T3=35 ºC son:
| > | datNIST:=p1=350e3*Pa_,h1=401.49e3*J_/kg_,p2=887e3*Pa_,T2s=38.3*degC,T2=42.8*degC,h2=425.65e3*J_/kg_,h3=247.93e3*J_/kg_,x4=0.21;mR_:=subs(datNIST,dat,QR_/(h1-h3));WR_:=subs(datNIST,dat,mR_*(h2-h1));eqetaR:=eta[R]=QR_/WR_;Wnet_:=rhs(eqBE_)-WR_; |
como se ve, apenas hay diferencia en prestaciones (pese a que el modelo sencillo predice una T2 mucho menor (apenas 36 ºC, frente a los casi 43 ºC reales.
| > |