>	restart:#"m18_p56"

Considérese un ciclo de refrigeración con R134a para evacuar 1 kW de una carga a 15 ºC ºC usando un compresor de rendimiento isoentrópico del 65 %, en un ambiente a 25 ºC, dejando un salto térmico mínimo de 5 ºC en los cambiadores. Se pide:
a) Coste energético y rendimiento (COP) en el límite de Carnot (con o sin el salto térmico mínimo)
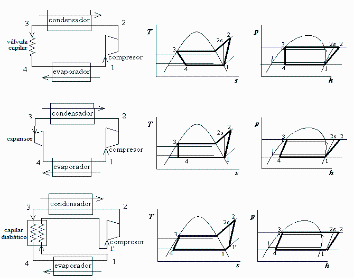
b) Coste energético y rendimiento de la máquina simple de R134a.
c) Coste energético y rendimiento en el caso de sustituir la válvula por un expansor isoentrópico.
d) Coste energético y rendimiento en el caso de que, antes de introducirlo en el compresor, se hiciese circular el vapor a contracorriente alrededor del tubo capilar que forma la válvula, tomando calor de éste hasta elevarse 5 ºC la temperatura del vapor.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(RealDomain):

>	su:="CF3CH2F":dat:=[QR=1e3*W_,T1=(-15+273.15)*K_,eta[C]=0.65,T0=(25+273.15)*K_,DT=5*K_];

>	dat:=op(dat),get_gas_data(su),get_liq_data(su),Const,SI2,SI1:get_pv_data(su):

a) Coste energético y rendimiento (COP) en el límite de Carnot (con o sin el salto térmico mínimo)

>	Tv1:=T1-DT;Tv1_:=subs(dat,%);'Tv1_'=TKC(%);Tv2:=T0+DT;Tv2_:=subs(dat,%);'Tv2_'=TKC(%);eta=Q2/W;eqCarnot:=eta=T1/(T2-T1);eqCarnotSin:=subs(T2=T0,dat,eqCarnot);WCsin:=subs(eqCarnotSin,dat,QR/eta);eqCarnotCon:=subs(T2=T0+DT,T1=T1-DT,dat,eqCarnot);WCcon:=subs(eqCarnotCon,dat,QR/eta);

	(1)

i.e. sin saltos, el COP de Carnot sería 6,5 y el consumo 155 W, y con los saltos sería eta=5,7 y W=174 W.

b) Coste energético y rendimiento de la máquina simple de R134a.

>

pv1_:=subs(dat,evalf(subs(dat,pv(Tv1_))));T1=Tv1_;pv2_:=subs(dat,evalf(subs(dat,pv(Tv2_))));T2:=T1*(1+((p2/p1)^((gamma-1)/gamma)-1)/eta[C]);T2_:=subs(T1=Tv1_,p1=pv1_,p2=pv2_,dat,%);'T2_'=TKC(%);h1_:=subs(dat,T=Tv1_,dat,hv(T));h2_:=subs(dat,T=T2_,dat,hv(T));h3_:=subs(dat,T=Tv2_,dat,hl(T));h4_:=h3_;eqetaR:=eta=(h1-h4)/(h2-h1);eqetaR_:=eta=(h1_-h4_)/(h2_-h1_);mR=QR/(h1-h4);mR_:=subs(dat,QR/(h1_-h4_));'mR_'=%*1000*g_/kg_;W=mR*(h2-h1);W_:=subs(dat,mR_*(h2_-h1_));

	(2)

i.e. con la máquina simple de R134a, sería COP=2,4 y W=414 W, circulando 6,8 g/s de R134a.

c) Coste energético y rendimiento en el caso de sustituir la válvula por un expansor isoentrópico.

Varía la h4.

>

s3_:=subs(dat,evalf(subs(dat,T=Tv2_,dat,sl(T))));s1l_:=subs(dat,evalf(subs(dat,T=Tv1_,dat,sl(T))));s1v_:=subs(dat,evalf(subs(dat,T=Tv1_,p=pv1_,dat,sv(T,p))));eqx4:=s3=(1-x4)*s1l+x4*s1v;x4_:=(s3_-s1l_)/(s1v_-s1l_);h4=(1-x4)*h1l+x4*h1v;h1l_:=subs(dat,T=Tv1_,dat,hl(T));h4_:=(1-x4_)*h1l_+x4_*h1_;eqetaR:=eta=(h1-h4)/(h2-h1-h3+h4);eqetaR_:=eta=(h1_-h4_)/(h2_-h1_-h3_+h4_);mR=QR/(h1-h4);mR_:=subs(dat,QR/(h1_-h4_)):'mR_'=%*1000*g_/kg_;W=mR*(h2-h1)-mR*(h3-h4);W_:=subs(dat,mR_*((h2_-h1_)-(h3_-h4_)));

	(3)

i.e. ahora no es h4=h3=164 kJ/kg sino h4=159 kJ/kg, y el COP aumenta de 2,4 a 2,5, reduciéndose el consumo desde 414 W a 363 W (y el flujo de 6,8 g/s a 6,6 g/s).

d) Coste energético y rendimiento en el caso de que, antes de introducirlo en el compresor, se hiciese circular el vapor a contracorriente alrededor del tubo capilar que forma la válvula, tomando calor de éste hasta elevarse 5 ºC la temperatura del vapor.

Ahora cambia también h4 pero por enfriamiento en el tubo capilar que hace de válvula. Habría que estudiar si el enfriamiento del capilar llega a subenfriar la entrada desde el condensador, que se supone saturada. Si no es así, la h3 no varía. El otro caso extremo sería que el enfriamiento tenga lugar en fase líquida justo tras el condensador y antes de entrar en el capilar. En la práctica suele haber un poco subenfriamiento en fase líquida con poca pérdida de presión, seguido de un subenfriamiento adicional metastable (también con poca caída de presión), y luego ya el ptoceso de vaporización con caída exponencial de presión debido al progresivo aumento de la velocidad del flujo bifásico (cada vez con mayor fracción de vapor y menor presión); la transmisión de calor es preponderante en esta región por el gran aumento del coeficiente convectivo por el interior del capilar, aunque el salto de temperatura hacia el vapor succionado por el compresor es menor.

Tomando el primer caso por ser el más sencillo, sean 1' y 2' los nuevos estados de entrada y salida del compresor.

>

T1p=T1+DT;T1p_:=subs(dat,T1+DT);T2p:=T1p*(1+((p2/p1)^((gamma-1)/gamma)-1)/eta[C]);T2p_:=subs(T1p=T1p_,p1=pv1_,p2=pv2_,dat,%);'T2p_'=TKC(%);h1p_:=subs(dat,T=T1p_,dat,hv(T));h2p_:=subs(dat,T=T2p_,dat,hv(T));h3_:=subs(dat,T=Tv2_,dat,hl(T));eqh4:=mR*(h3-h4)=mR*(h2p-h1);h4_:=h3_-(h1p_-h1_);eqetaR:=eta=(h1-h4)/(h2p-h1p);eqetaR_:=eta=(h1_-h4_)/(h2p_-h1p_);mR=QR/(h1-h4);mR_:=subs(dat,QR/(h1_-h4_));'mR_'=%*1000*g_/kg_;W=mR*(h2p-h1p);W_:=subs(dat,mR_*(h2p_-h1p_));

	(4)

i.e. con el capilar diabático ya no es h4=h3=164 kJ/kg sino h4=156 kJ/kg, y el COP aumenta de 2,40 a 2,45, reduciéndose el consumo desde 414 W a 407 W.

>

>