>	restart:#"m18_p42"

Se quiere obtener una corriente de 1 kg/s de aire hasta -25 ºC a partir del ambiente, que se supondrá a 20 ºC y 94 kPa. Para ello se piensa usar una máquina refrigerante de compresión de vapor de NH3 (R-717), con presiones máxima y mínima de 1 MPa y 0,1 MPa, con un compresor de rendimiento isoentrópico 0,8. Se pide:

a) Calor a evacuar, y potencia mecánica mínima necesaria para refrigerar el aire (límite termodinámico).

b) Temperaturas de cambio de fase del NH3, saltos térmicos en los cambiadores, y diagramas T-s y p-h de la evolución.

c) Potencia demandada por el compresor, temperatura a la salida, y gasto másico de refrigerante necesario.

d) Determinar, usando el modelo de sustancia perfecta, la fracción másica de vapor de NH3 a la salida de la válvula.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aire":su2:="NH3":dat:=[ma=1*kg_/s_,Ta2=(-25+273.15)*K_,Ta1=(20+273.15)*K_,T0=(20+273.15)*K_,p1=94e3*Pa_,p1=0.1e6*Pa_,p2=1e6*Pa_,etaC=0.8];

>	Adat:=get_gas_data(su1):Rdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):dat:=[op(dat),Const,SI2,SI1]:

a) Calor a evacuar, y potencia mecánica mínima necesaria para refrigerar el aire (límite termodinámico).

Se supone aire seco, pues si no habría problemas de formación de hielo.

El trabajo mínimo es la exergía de la corriente (respecto al ambiente).

>	T0=subs(dat,Ta1);p0=subs(dat,p0);QdotR:=ma*c[p]*(Ta1-Ta2);QdotR_:=subs(dat,Adat,dat,QdotR);Wdot_min:=ma*(psi2-psi1);Wdot_min:=ma*(h2-h1-T0*(s2-s1));Wdot_min:=ma*(c[p]*(Ta2-Ta1)-T0*(c[p]*ln(Ta2/Ta1)-R*ln(pa2/pa1)));pa2:=pa1;Wdot_min_:=subs(dat,evalf(subs(Adat,dat,Wdot_min)));

i.e. hay que evacuar 45 kW en forma de calor, para lo que hará falto aportar un mínimo de 3,9 kW de trabajo.

b) Temperaturas de cambio de fase del NH3, saltos térmicos en los cambiadores, y diagramas T-s y p-h de la evolución.

Usando la Ec. de Anyoine:

>	T1:=Tv(p1);T1:=evalf(subs(dat,solve(pv(T)=subs(dat,p1),T)));'T1'=TKC(%);T3:=evalf(subs(dat,solve(pv(T)=subs(dat,p2),T)));'T3'=TKC(%);

i.e. en el vaporizador hierve a T1=238 K (-35 ºC; bueno mejor a 240 K=-33 ºC que es la temperatura de ebullición normal que viene en las tablas), con un salto de -25-(-33)=8 K desde la temperatura del refrigerante hasta la temperatura mínima del aire, apropiado para la transmisión de calor.

En el condensador condensa a T3=298 K (25 ºC), con un salto de 25-20=5 ºC sobre la temperatura ambiente, apropiado para la transmisión de calor si se ayuda con un ventilador.

(Diagramas arriba.)

c) Potencia demandada por el compresor, temperatura a la salida, y gasto másico de refrigerante necesario.

Del balance energético del vaporizador:

>

eqEB41:='QdotR=mdotR*(h1-h4)';'QdotR'=QdotR_;h1=hv(p1);h1:=subs(Rdat,T=T1,Rdat,hv(T));h3:=subs(Rdat,T=T3,Rdat,hl(T));h4:=h3;mR:=subs(dat,QdotR_/(h1-h4));Wdot:='mR*c[p]*(T2-T1)';T2_:='T1*(1+((p2/p1)^((gamma-1)/gamma)-1)/etaC)';cpR:=subs(Rdat,c[p]);gammaR:=subs(Rdat,gamma);T2:=subs(Rdat,dat,T2_);'T2'=TKC(%);Wdot_:=subs(c[p]=cpR,dat,Wdot);

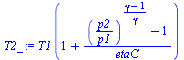i.e., para evacuar los 45 kW hace falta un flujo de NH3 de 0,042 kg/s, y el compresor necesita 19 kW, comprimiendo el gas hasta 445 K (171 ºC).

d) Determinar, usando el modelo de sustancia perfecta, la fracción másica de vapor de NH3 a la salida de la válvula.

>	eqx:='h4=(1-x4)*h4l+x4*h4v';h4l:=subs(Rdat,T=T1,Rdat,hl(T));h4v:='h1';x4:=solve(eqx,x4);

i.e. x4=0.20 (un 20% de fracción másica de vapor).

Con datos del NIST, T1=239,6 K, T3=298,1 K, h1=1561 kJ/kg, h3=460,3 kJ/kg, s1=6598 J/(kg·K), h2s=1907 kJ/kg, h2=1994 kJ/kg, T2=441,5 K (168 ºC), mR=Q(h1-h3)=0,041 kg/s, W=mR(h2-h1)=17,7 kW, x4=0,197.

>