>	restart:#"m18_p37"

Un equipo de aire acondicionado debe tomar 0,25 kg/s de aire de un local a 25 ºC, y enfriarlo hasta 5 ºC. Sabiendo que la potencia de refrigeración necesaria para ese cometido (teniendo en cuenta la condensación del aire húmedo) es de 11 kW, que se va a usar una máquina de R134a con saltos mínimos de 5 ºC en los cambiadores, y que el aire ambiente está a 35 ºC, se pide:
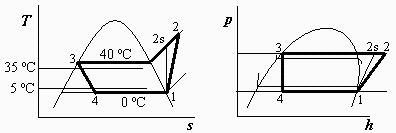
a) Esquema de los procesos en el diagrama T-s, indicando los valores de las temperaturas representativas.
b) Calcular el gasto másico de gas circulante requerido, usando el modelo de sustancia perfecta (MSP).
c) Calcular la potencia necesaria del compresor (tómese un rendimiento del 75%), y la eficiencia energética de la máquina (modelo MSP).
d) Volver a resolver el problema con ayuda del diagrama p-h del R134a.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="CF3CH2F":dat:=[TR=(5+273.15)*K_,QR=11e3*W_,DT=5*K_,T0=(35+273.15)*K_,etaC=0.75];

>	dat:=op(dat),get_gas_data(su),get_liq_data(su),Const,SI2,SI1:get_pv_data(su):

a) Esquema de los procesos en el diagrama T-s, indicando los valores de las temperaturas representativas.

(Ver arriba.)

Nótese que la máquina ha de trabajar entre el foco frío y el ambiente, independientemente de las condiciones de entrada del aire.

>	T1:=TR-DT;T1_:=subs(dat,%);'T1'=TKC(%);T3:=T0+DT;T3_:=subs(dat,%);'T3'=TKC(%);p1_:=evalf(subs(T=T1_,pv(T)));p2_:=evalf(subs(T=T3_,pv(T)));

i.e., el vaporizador debe estar a 0 ºC (0,3 MPa), y el condensador a 40 ºC (1 MPa).

b) Calcular el gasto másico de gas circulante requerido, usando el modelo de sustancia perfecta (MSP).

Será QR=mR*(h1-h4).

>	eqBEvap:='QR'=mR*(h1-h4);h1_:=subs(dat,T=T1_,dat,hv(T));h3_:=subs(dat,T=T3_,dat,hl(T));h4=h3;mR_:=subs(dat,QR/(h1_-h3_));

i.e. hay que hacer circular 73 g/s de R134a.

c) Calcular la potencia necesaria del compresor (tómese un rendimiento del 75%), y la eficiencia energética de la máquina (modelo MSP).

>	WR:='mR*c[p]*(T2-T1)';T2s:='T1*(p2/p1)^((gamma-1)/gamma)';T2s_:=subs(p2=p2_,p1=p1_,dat,%);eqetaC:=eta='(T2s-T1)/(T2-T1)';T2_:=subs(dat,T1_+(T2s_-T1_)/etaC);WR_:=subs(dat,mR_*c[p]*(T2_-T1));eqetaR:=eta='QR/WR';subs(dat,eta=QR/WR_);

i.e. el compresor consumirá 2,9 kW, y la eficiencia energética de refrigeración es de 3,8.

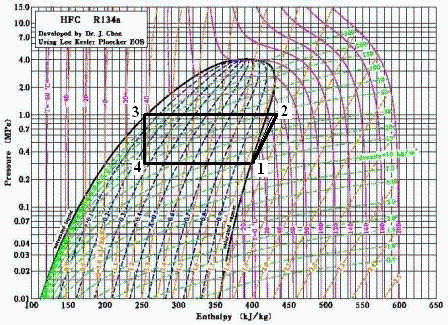
d) Volver a resolver el problema con ayuda del diagrama p-h del R134a.

Tomando valores del diagrama adjunto:

>	p1:=1e6*Pa_;p2:=0.3e6*Pa_;h1:=400e3*J_/kg_;s1:=1860*J_/(kg_*K_);h3:=250e3*J_/kg_;h2s:=430e3*J_/kg_;h2:=subs(dat,h1+(h2s-h1)/etaC);mR:=subs(dat,QR/(h1-h3));WR:=subs(dat,mR*(h2-h1));eta=subs(dat,QR/WR);

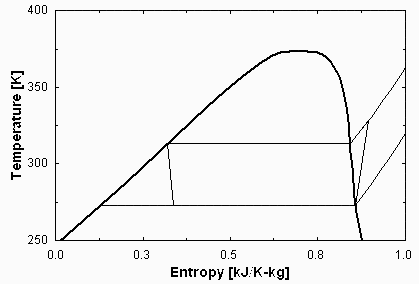
Con los datos más precisos del NIST:

>	p1:=1013e3*Pa_;p2:=291.2e3*Pa_;h1:=232.7e3*J_/kg_;s1:=858.1*J_/(kg_*K_);h3:=90.38e3*J_/kg_;T2s:=317.5*K_;h2s:=258.8e3*J_/kg_;h2:=subs(dat,h1+(h2s-h1)/etaC);mR:=subs(dat,QR/(h1-h3));WR:=subs(dat,mR*(h2-h1));eta=subs(dat,QR/WR):evalf(%,2);

En resumen, el modelo MSP es sencillo y versátil, y no predice mal: 2,9 kW para el compresor, en vez del más exacto 2,7 kW (la incertidumbre en el valor del rendimiento isoentrópico puede que sea mayor). La resolución gráfica, si el diagrama de propiedades está disponible, es la más directa y cómoda (la precisión depende del tamaño del gráfico). La solución programada con datos precisos es la más exacta, pero no es versátil (sólo vale para resolver problemas estándar), y, si no se controlan sus resultados puede ser arriesgada (no saber si es válida, o siquiera razonable).

>