>	restart:#"m18_p33"

Para un túnel de congelación, se quiere obtener un flujo de 1 kg/s de aire a -35 ºC a partir de aire ambiente a 20 ºC. Se piensa usar una máquina de refrigeración por compresión mecánica de vapor de amoniaco con rendimiento isoentrópico del compresor del 75% y 5 ºC de salto mínimo en los cambiadores. Se pide:
a) Determinar el calor a evacuar y el trabajo mínimo necesario (límite termodinámico).
b) Determinar las presiones de funcionamiento de la máquina.
c) Determinar las entalpías en los puntos característicos del ciclo.
d) Determinar el flujo de refrigerante necesario.
e) Determinar el consumo del compresor.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aire":su2:="NH3":dat:=[ma=1*kg_/s_,Tload=(-35+273)*K_,T0=(20+273)*K_,eta=0.75, DT=5*K_];

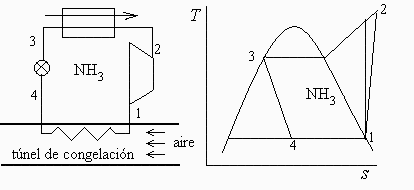
Esquema:

>

>

Eqs. const.:

>	Adat:=get_gas_data(su1):Rdat:=get_gas_data(su2),get_liq_data(su2):dat:=op(dat),Const,SI2,SI1:get_pv_data(su2):[M,c[p],rho,c,T[b],h[lv0]]=subs(Rdat,[M,c[p],rho,c,T[b],h[lv0]]);p[v](T)=pv(T);

a) Determinar el calor a evacuar y el trabajo mínimo necesario (límite termodinámico).

>	QR:=ma*Dh;QR:=ma*c[p]*(T0-Tload);QR_:=subs(Adat,dat,QR);Wmin:=ma*(Dh-T0*Ds);Wmin:=ma*(c[p]*(Tload-T0)-T0*c[p]*ln(Tload/T0));Wmin_:=subs(dat,evalf(subs(Adat,dat,Wmin)));

i.e. hay que evacuar 55 kW, y el coste mínimo es de 5,9 kW.

El aire deberá estar suficientemente seco para que no se forme escarcha, o disponer de un sistema apropiado de desescarchado.

b) Determinar las presiones de funcionamiento de la máquina.

>	T1:=Tload-DT;T1_:=subs(dat,%);p1_:=subs(dat,evalf(pv(T1_)));T3:=T0+DT;T3_:=subs(dat,%);p2_:=subs(dat,evalf(pv(T3_)));

i.e. el compresor trabajará entre 70 kPa y 1,0 MPa.

c) Determinar las entalpías en los puntos característicos del ciclo.

Tomando como nivel de referencia h=0 y s=0 para la fase líquida en el punto triple:

>	h[L]=hl(T);h[V]=hv(T);h3_:=subs(Rdat,T=T3_,dat,hl(T));h4_:=h3_;h1_:=subs(Rdat,T=T1_,dat,hv(T));gamma=subs(Rdat,gamma);eq5_59;T2_:=subs(Rdat,dat,T1_*(1+((p2_/p1_)^((gamma-1)/gamma)-1)/eta));h2_:=subs(Rdat,T=T2_,dat,hv(T));

NOTA: los valores de h dependen del estado de referencia (no así sus diferencias).

d) Determinar el flujo de refrigerante necesario,

>	mR:='QR/(h1-h4)';mR_:=subs(dat,QR_/(h1_-h4_));

e) Determinar el consumo del compresor.

>	WC:='mR*(h2-h1)';WC_:=subs(dat,mR_*(h2_-h1_));

i.e. el compresor consume 28 kW (mucho más de los 6 kW de mínimo).

Si se usan los datos del NIST para el NH3, los resultados serían:

A 233 K, pv=71,12 kPa, y a 298 K, pv=998,6 kPa.

h1=1359 kJ/kg, h2s=1764 kJ/kg, h2=1899 kJ/kg, h3=h4=-30,26 kJ/kg. T2s=425.9 K y T2=480,4 K.

mR=0.0397.

WC=21,5 kW.

Conclusión: El modelo de sustancia perfecta puede ser adecuado para una primera aproximación, pues aunque el eroor en el cálculo de la potencia del compresor es de un 30%, es por el lado conservativo.

>	h2:=(1359+(1764-1359)/0.75)*1e3*J_/kg_;mR:=(55.2/(1359-(-30.26)))*kg_/s_;WC:=subs(dat,mR*(1899-1359)*1e3*J_/kg_);

>