>	restart:#"m18_p13"

Para un sistema de acondicionamiento de aire se utiliza una bomba térmica de R 12 cuyo compresor (volumétrico) tiene 1 litro de cilindrada total, funciona a 3000 rpm y da una relación de presiones de 4, suponiéndose que tanto el rendimiento volumétrico como el isoentrópico son la unidad. El aire se toma de la atmósfera a 94 kPa, 5 °C y 20% de humedad relativa y, tras pasar por la bomba de calor y por un humidificador adiabático, sale a 23 °C. Sabiendo que los cambiadores de calor de la bomba requieren un salto mínimo de 5 °C y que ésta incorpora un intercambiador para subenfriar el condensado y a la vez sobrecalentar el vapor de R 12 en 5 °C antes de la entrada al compresor, se pide;
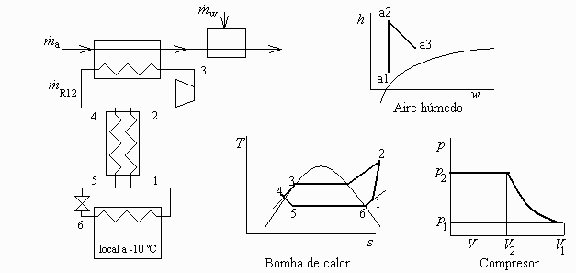
a) Esquema de las evoluciones de R 12 y el aire húmedo en los diagramas T s y h w, respectivamente.
b) Potencia necesaria, eficiencia energética y exergética de la bomba.
c) Gasto de aire.
d) Humedad relativa del aire a la salida y consumo de agua.
e) Trabajo mínimo necesario disponiendo libremente de la atmósfera..
Datos::

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="CCl2F2":su2:="H2O":su3:="Aire":dat:=[V1=1e-3*m_^3,N=(3000/60)/s_,pi[12]=4,p0=94e3*Pa_,T0=(5+273)*K_,phi0=0.2,Ta3=(23+273)*K_,DT=5*K_];

Esquema:

>	Sistemas:=[compresor,cambiadores,válvula,humidificador_adiabático]:

>	Componentes:=[CCl2F2, Aire]:

>	Estados:=[1,2,3,4,5,6,a1,a2,a3]:

>	dat:=op(dat),Const,SI2,SI1:R12dat:=get_gas_data(su1),get_liq_data(su1):pvR12:=get_pv_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):Adat:=get_gas_data(su3):

a) Esquema de las evoluciones de R 12 y el aire húmedo en los diagramas T s y h w, respectivamente.

>

b) Potencia necesaria, eficiencia energética y exergética de la bomba.

La potencia necesaria es la del compresor volumétrico, que tome una masa m1 de vapor de R12 en condiciones (p1,T1) y la suelta en condiciones (p2,T2), con p2/p1=pi12 y T2/T1=1+(pi12^((g-1)/g)-1)/eta, pero no en regimen continuo sino N veces por segundo.

El trabajo en una embolada es el recibido por el fluido en la compresión adiabática W=m1*cv*(T2-T1) más el recibido por el fluido para su expulsión W=p2*V2, menos el realizado por la atmósfera en total W=p1*V1.

>

Wdot:=N*(m1*c[v]*(T2-T1)+p2*V2-p1*V1);Wdot:=N*m1*c[p]*(T2-T1);Wdot:=N*((p1*V1)/(R*T1))*c[p]*T1*(pi[12]^((gamma-1)/gamma)-1);p1=p[v](T1);T1=T0-DT[cambiad]+DT[sobre];T1_:=subs(dat,T0-DT+DT);p1_:=evalf(subs(T=T1_,pvR12(T))):'p1'=evalf(%,2);p2=p1*pi[12];p2_:=subs(dat,p1_*pi[12]):'p2'=evalf(%,2);Wdot_:=subs(dat,evalf(subs(p1=p1_,R12dat,dat,Wdot))):'Wdot'=evalf(%,2);

Ahora resolvemos la bomba de calor. Usamos el modelo de sustancia perfecta. Ver nomenclatura en Fig. 1.

>

h1_:=subs(R12dat,T=T1_,dat,hv(T)):'h1'=evalf(%,2);T2:=subs(eta[C]=1,T1*(1+((p2/p1)^((gamma-1)/gamma)-1)/eta[C]));T2_:=subs(T1=T1_,p1=p1_,p2=p2_,R12dat,T2):'T2'=evalf(%,3);h2_:=subs(R12dat,T=T2_,dat,hv(T)):'h2'=evalf(%,2);T3:=Ta3+DT;T3_:=subs(dat,T3);h3_:=subs(R12dat,T=T3_,dat,hl(T)):'h3'=evalf(%,2);mR12:=Wdot/(h2-h1);mR12_:=subs(dat,Wdot_/(h2_-h1_)):'mR12'=evalf(%,2);T6=T0-DT;T6_:=subs(dat,T0-DT);h6_:=subs(R12dat,T=T6_,dat,hv(T)):'h3'=evalf(%,2);eqBEHX:=h3-h4=h1-h6;h4_:=h3_-(h1_-h6_):'h4'=evalf(%,2);h5:=h4;Qa:='mR12*(h2-h3)';Qa_:=subs(dat,mR12_*(h2_-h3_)):'Qa'=evalf(%,2);

Las eficiencias energéticas y exergéticas de la bomba son:

>	eqetae:=eta[e]='Qa/Wdot';eqetae_:=eta[e]=Qa_/Wdot_:evalf(%,2);eqetax:=eta[x]=eta[e]/eta[Carnot];eqetaC:=eta[Carnot]=Ta3/(Ta3-T0);eqetaC_:=eta[Carnot]=subs(dat,Ta3/(Ta3-T0)):evalf(%,2);eqetax_:=subs(eqetae_,eqetaC_,eqetax):evalf(%,2);

donde la referencia de Carnot se ha tomado entre el ambiente a 5 ºC y el objetivo de disponer de una fuente a 23 ºC, aunque se podrñia haber tomado el de calentar la corriente directamente.

c) Gasto de aire.

>	eqBEcond:='ma*c[p]*(Ta2-Ta1)=Qa';eqBEcond:='ma*(ha3-ha1)=Qa';h=h(T,w);w=w(phi,T,p);Ta1:=T0;phi1:=phi0;w1_:=subs(dat,evalf(subs(dat,w(phi1,Ta1,p0)))):'w1'=evalf(%,2);ha1_:=subs(c[pa]=c[p],Adat,c[pv]=c[p],Wdat,T=T0,dat,h(T,w1_)):'ha1'=evalf(%,2);

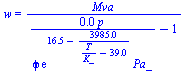NOTA. No queda determinada la solución de encontrar ma y phi3, pues sólo se dispone del balance energético (el másico daría luego el mw).

Supongamos que se desea que salga con phi3=0.5.

>	phi3_:=0.5;w3_:=subs(dat,evalf(subs(dat,w(phi3_,Ta3,p0)))):'w3'=evalf(%,2);ha3_:=subs(c[pa]=c[p],Adat,c[pv]=c[p],Wdat,T=Ta3,dat,h(T,w3_)):'ha3'=evalf(%,2);ma:='Qa'/(ha3-ha1);ma_:=subs(dat,Qa_/(ha3_-ha1_)):'ma'=evalf(%,2);

d) Humedad relativa del aire a la salida y consumo de agua.

>	'phi3'=phi3_;meqBMw:='ma*w1+mw=ma*w3';mw_:=ma_*(w3_-w1_):'mw'=evalf(%,2);

e) Trabajo mínimo necesario disponiendo libremente de la atmósfera.

Se trata de obtener una corriente ma de aire húmedo (phi3,T3a,p0) a partir del aire ambiente (phi0,T0,p0), obteniendo también el agua de allí. Por unidad de gasto molar

Si los flujos molares de aire seco y vapor de agua son na y nv, el trabajo mínimo (la exergía de la corriente) es:

>

Phi03:=n*xa3*(c[pa]*(Ta3-T0)-T0*(c[pa]*ln(Ta3/T0)+R[u]*ln(xa3/xa0)))+n*xv3*(c[pv]*(Ta3-T0)-T0*(c[pv]*ln(Ta3/T0)+R[u]*ln(xv3/xv0)))+n*R[u]*ln(p3/p0);x[v]=phi*p[v](T)/p;xv0_:=evalf(subs(dat,phi0*pv(T0)/p0)):'xv0'=evalf(%,2);xa0_:=1-xv0_:'xa0'=evalf(%,2);xv3_:=evalf(subs(dat,phi3_*pv(T3_)/p0)):'xv3'=evalf(%,2);xa3_:=1-xv3_:'xa3'=evalf(%,2);na:='ma/M[a]';na_:=subs(Adat,dat,ma_/M):'na'=evalf(%,2);nv:='xv3*na';nv_:=xv3_*na_:'nv3'=evalf(%,2);

>	Phi03a:=n*xa3*(c[pa]*(Ta3-T0)-T0*(c[pa]*ln(Ta3/T0)));Phi03b:=n*xv3*(c[pv]*(Ta3-T0)-T0*(c[pv]*ln(Ta3/T0)));Phi03c:=n*R[u]*T0*(ln(p3/p0)+xa3*ln(xa3/xa0)+xv3*ln(xv3/xv0));

>

Phi03a_:=subs(dat,evalf(subs(dat,Adat,na_*xa3_*(c[p]*M*(Ta3-T0)-T0*(c[p]*M*ln(Ta3/T0)))))):'Phi03a'=evalf(%,2);Phi03b_:=subs(dat,evalf(subs(dat,Wdat,na_*xv3_*(c[p]*M*(Ta3-T0)-T0*(c[p]*M*ln(Ta3/T0)))))):'Phi03b'=evalf(%,2);Phi03c_:=subs(dat,na_*R[u]*T0*(ln(p0/p0)+xa3_*ln(xa3_/xa0_)+xv3_*ln(xv3_/xv0_))):'Phi03c'=evalf(%,2);Phi03_:=Phi03a_+Phi03b_+Phi03c_:'Phi03'=evalf(%,2);

i.e., el límite termodinámico es de 13 kW. Aquí se han gastado 27 kW más la exergía asignable al agua de aporte.

>