>	restart:#"m18_p12"

En una piscina cubierta climatizada se necesita renovar 1,3 kg/s de aire. La entrada del exterior es a 5 °C, =0,2, y la salida a 29 °C, =0,98, siendo la presión ambiente 90 kPa. Para ahorrar combustible se piensa utilizar una bomba de calor de R 12, para recuperar el calor del aire eliminado. El compresor de la bomba es movido por un motor de explosión de cuatro tiempos que funciona a 1500 rpm, tiene una cilindrada de 950 cm3, una relación de compresión de 9, y alcanza una presión máxima de 40 bar. Se desea calcular:
a) Energía que hay que aportar en ausencia de la bomba de calor.
b) Calor que debe proporcionar el combustible en el motor y trabajo al eje.
c) Calor que es capaz de bombear la bomba de calor.
d) Energía que hay que aportar, en total, usando la bomba de calor, sabiendo que el 90% del calor evacuado por el motor (refrigeración más escape) es aprovechado también mediante un cambiador de calor para calentar el aire a la entrada de la piscina.
Datos::

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="CCl2F2":su2:="H2O":su3:="Aire":dat:=[ma=1.3*kg_/s_,Ta1=(5+273)*K_,phi1=0.2,Ta3=(29+273)*K_,phi3=0.98,p0=90e3*Pa_,N=(1500/60)/s_,V=950e-6*m_^3,r=9,pmax=40e5*Pa_,eta[Rec]=0.9];

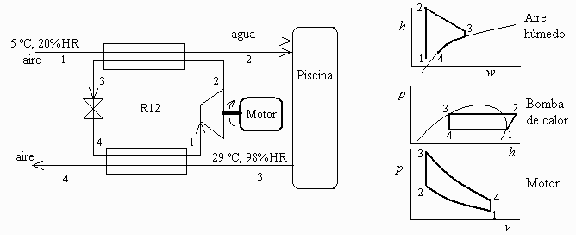
Esquema:

>	Sistemas:=[compresor,cambiadores,válvula,motor,piscina]:

>	Componentes:=[Aire_humedo,CCl2F2,Aire_estandar]:

>	Estados:=[1,2,3,4]:# Para cada circuito: aire húmedo, refriferante, aire estándar.

>	dat:=op(dat),Const,SI2,SI1:R12dat:=get_gas_data(su1),get_liq_data(su1):pvR12:=get_pv_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):Adat:=get_gas_data(su3):

a) Energía que hay que aportar en ausencia de la bomba de calor.

No se consideran aportes energéticos dentro del recinto de la piscina.

No se tiene en cuenta la entalpía del agua de aporte en el balance energético.

Se aproxima el gasto de aire de entrada al gasto de aire seco, ma.

La energía que hay que aportar en ausencia de la bomba de calor será:

>

eqBE:=Qa=ma*(ha2-ha1);ha2:=ha3;h=h(T,w);eq8_8;;w1_:=subs(dat,evalf(subs(dat,w(phi1,Ta1,p0)))):'w1'=evalf(%,2);w3_:=subs(dat,evalf(subs(dat,w(phi3,Ta3,p0)))):'w3'=evalf(%,2);ha1_:=subs(c[pa]=c[p],Adat,c[pv]=c[p],Wdat,T=Ta1,dat,h(T,w1_)):'ha1'=evalf(%,2);ha3_:=subs(c[pa]=c[p],Adat,c[pv]=c[p],Wdat,T=Ta3,dat,h(T,w3_)):'ha3'=evalf(%,2);Qa:=ma*(ha3-ha1);Qa_:=subs(dat,ma*(ha3_-ha1_)):'Qa'=evalf(%,2);

i.e., hay que comunicar al aire 98 kW, además de añadirle agua:

>	eqBMw:=mw=ma*(w3-w2);w2:=w1;eqBMw:=subs(w3=w3_,w1=w1_,dat,eqBMw):evalf(%,2);

i.e. el aire recibe 0,035 kg/s de agua de la piscina.

b) Calor que debe proporcionar el combustible en el motor y trabajo al eje.

El motor es para mover el compresor, así que hay que resolver el ciclo de R12 primero, para ver cuánto trabajo necesita.

Aunque en la práctica habrá que dejar un poco de salto térmico en el evaporador y condensador, no lo consideramos aquí.

El condensador ha de trabajar como mínimo a 29 ºC.

El evaporador ha de trabajar a bastante menos de 29 ºC para poder tomar el calor. En lugar de optimizar de entrada, supongamos que la Tevap=15 ºC y luego veremos si es posible y si queda margen para optimizar.

Resolvamos el refrigerador. Usaremos el modelo de sustancia perfecta.

>

T1_:=288*K_;T3_:=subs(dat,Ta3);p1_:=pvR12(T1_):'p1'=evalf(%,2);p2_:=pvR12(T3_):'p2'=evalf(%,2);h1_:=subs(R12dat,T=T1_,dat,hv(T)):'h1'=evalf(%,2);T2:=subs(eta[C]=1,T1*(1+((p2/p1)^((gamma-1)/gamma)-1)/eta[C]));T2_:=subs(T1=T1_,p1=p1_,p2=p2_,R12dat,T2):'T2'=evalf(%,3);h2_:=subs(R12dat,T=T2_,dat,hv(T)):'h2'=evalf(%,2);h3_:=subs(R12dat,T=T3_,dat,hl(T)):'h3'=evalf(%,2);mR12:=Qa/(h2-h3);mR12_:=subs(dat,Qa_/(h2_-h3_)):'mR12'=evalf(%,2);Wcomp:='mR12*(h2-h1)';Wcomp_:=subs(dat,mR12_*(h2_-h1_)):'Wcomp'=evalf(%,2);

Ahora, resolvamos el motor de explosión.

>

T2:='T2':Wnet:=(N/2)*rho*V*(w34-w12);eqET:=rho=subs(Adat,dat,p0/(R*T0)):evalf(%,2);w12:=c[v]*(T2-T1);w12:=c[v]*T0*(r^(gamma-1)-1);w12_:=subs(Adat,dat,w12):'w12'=evalf(%,2);w34:=c[v]*(T3-T4);w34:=c[v]*T3*(1-1/r^(gamma-1));T3=T2*pmax/p2;T3=(T0*r^(gamma-1))*pmax/(p0*r^gamma);T3:=T0*(pmax/p0)/r;T3_:=subs(dat,T3):'T3'=evalf(%,3);w34_:=subs(Adat,dat,c[p]*T3_*(1-1/r^(gamma-1))):'w34'=evalf(%,2);Wnet_:=subs(eqET,dat,(N/2)*rho*V*(w34_-w12_)):'Wnet'=evalf(%,2);

Resulta que, suponiendo el motor ideal, daría un trabajo al eje de 7 kW, y el compresor (que también se ha supuesto ideal) demandaría 5.4 kW. La combinación puede ser aceptable porque un motor real dará menos potencia (ya las pérdidas por fricción pueden ser del 10%) y un compresor real consumirá más potencia..

El consumo de combustible de ese motor ideal vendría dado por:

>	eqeta:='Wnet/Qcomb=1-1/r^(gamma-1)';Qcomb_:=subs(Adat,dat,Wnet_/(1-1/r^(gamma-1))):'Qcomb'=evalf(%,2);mF:='Qcomb/PCI';PCI:=40e6*J_/kg_;mF_:=subs(dat,Qcomb_/PCI):'mF'=evalf(%,2);

c) Calor que es capaz de bombear la bomba de calor.

Con un compresor ideal de 5,4 kW la bomba ya suministraría los 98 kW necesarios al ire de entrada.

d) Energía que hay que aportar, en total, usando la bomba de calor, sabiendo que el 90% del calor evacuado por el motor (refrigeración más escape) es aprovechado también mediante un cambiador de calor para calentar el aire a la entrada de la piscina.

Si ya se calienta el aire de entrada con los gases y el agua del motor, la bomba de calor puede ser más pequeña.

>	eqRec:='Q_Rec=ma*c[p]*(Tai-Ta1)';Q_rec:='(Qcomb-Wnet)*eta[Rec]';Q_Rec_:=subs(dat,(Qcomb_-Wnet_)*eta[Rec]):'Q_Rec'=evalf(%,2);Tai_:=subs(Adat,dat,Ta1+Q_Rec_/(ma*c[p])):'Tai'=evalf(%,3);

En efecto, se podrían aprovechar hasta 4,5 kW de energía sobrante del motor, con la que se calentaría fácilmente el aire desde 5 ºC hasta 11 ºC, y la bomba ya sólo tendría que aportar Qa-Q_Rec=94 kW en vez de los 98 kW, con lo que ahora sólo consumiría5,4*(94/98)=5,2 kW en vez de 5,4 kW, pues es lineal.

En resumen, hay que aportar unos 12 kW de energía del combustible (al motor) para que funcione toda la instalación; un ahorro muy considerable, frente a los más de 98 kW de combustible si se quemase en una caldera (pero hay que comprar el motor y la bomba de calor).

Nótese que al recuperar el calor del aire húmedo a la salida, éste se saturará y condensará agua (hasta el punto 4 del diagrama del aire húmedo esquematizado).