>	restart:#"m18_p08"

Se desea obtener 20 kg/h de etileno líquido a 100 kPa a partir de gas a 30 °C y 100 kPa. El etileno (gas) se comprime isotérmicamente hasta 1 MPa. La expansión tiene un rendimiento adiabático de 0,6, y el gas que sale del licuador regresa a la entrada del equipo de compresores a temperatura ambiente. Se pide:
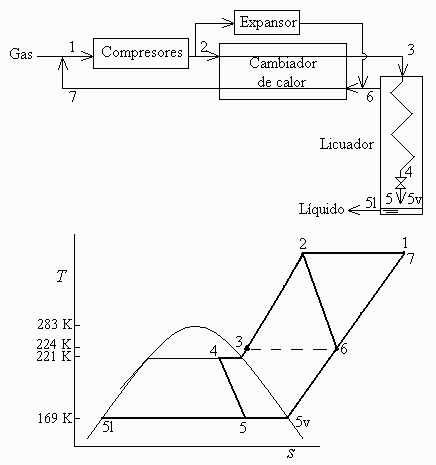
a) Representación del proceso en el diagrama T s.
b) Potencia mínima necesaria teniendo como única fuente térmica la atmósfera.
c) Potencia necesaria para la compresión.
d) Temperatura a la salida del expansor.
e) Sabiendo que se va a obligar a que la temperatura de entrada al licuador sea la misma que la de salida del expansor, calcular la fracción licuada.
f) Fracción que debe ser derivada hacia el expansor para conseguir las condiciones expuestas en e).
g) Potencia real consumida.
Datos::

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="C2H4":dat:=[ml=(20/3600)*kg_/s_,T0=(30+273)*K_,p2=1e6*Pa_,eta[E]=0.6]:evalf(%,2);

Esquema:

>

>

>	Estados:=[1,2,3,4,5,6,7]:

>	Edat:=get_gas_data(su1),get_liq_data(su1):evalf([%],3);dat:=op(dat),Edat,Const,SI2,SI1:get_pv_data(su1):

a) Representación del proceso en el diagrama T s.

Lo de la expansión significa que se trata de un proceso Claude, como el esquematizado en la Fig. 1, en lugar del método Linde.

Ver arriba.
b) Potencia mínima necesaria teniendo como única fuente térmica la atmósfera.

Usando el modelo de sustancia perfecta:

>	Wmin:=m*Dphi;Wmin:=m*(Dh-T0*Ds);Dh:=-h[lv0]+c[p]*(T[b]-T0);Ds:=-h[lv0]/T[b]+c[p]*ln(T[b]/T0);Dh_:=subs(dat,Dh):'Dh'=evalf(%,2);Ds_:=subs(dat,evalf(subs(dat,Ds))):'Ds'=evalf(%,2);ml_:=subs(dat,ml):'ml'=evalf(%,2);Wmin_:=subs(dat,ml_*(Dh_-T0*Ds_)):'Wmin'=evalf(%,2);

i.e. el coste mínimo es de 2,5 kW para los 20 kg/h de líquido (450 kJ/kg de líquido obtenido).

c) Potencia necesaria para la compresión

>	p1:=p0;T1:=T0;T2:=T1;Wisot:=Wmin12;Wisot:=m*(Dh12-T0*Ds12);Wisot:=m*(c[p]*(T2-T1)-T0*(c[p]*ln(T2/T1)-R*ln(p2/p1)));wisot_:=subs(dat,evalf(subs(dat,Wisot/m))):'wisot'=evalf(%,2);

i.e., 210 kJ/kg de gas.

Nótese que no se puede poner m=ml porque habrá que comprimir mucho gas para licuar un poco.

La compresión isoterma es impracticable, pero se puede aproximar con múltiples compresiones con enfriamiento intermedio.

d) Temperatura a la salida del expansor.

Con el modelo de gas perfecto para la expansión en una turbina:

>	eqetaE:='eta[E]=(1-T1/T2)/(1-(p1/p2)^((gamma-1)/gamma))';eqetaE:=eta[E]=(1-T2/T6)/(1-(p2/p6)^((gamma-1)/gamma));T6_:=subs(p6=p0,dat,solve(%,T6)):'T6'=evalf(%,3);Tvp2_:=subs(dat,evalf(subs(dat,solve(p2=pv(T),T)))):'Tvp2'=evalf(%,3);

e) Sabiendo que se va a obligar a que la temperatura de entrada al licuador sea la misma que la de salida del expansor, calcular la fracción licuada.

Con el modelo de sustancia perfecta:

>	T3:=T6;eqBE_L:=h3=(1-x5)*h5l+x5*h6;x5_:=solve(%,x5);'x5'=simplify(subs(h3=h6,%));

i.e. el modelo de sustancia perfecta no es aplicable; hay que corregir por efectos de compresibilidad, sea por el método de estados correspondientes, o a partir de datos gráficos o tabulados del comportamiento real del etileno.

Tomando los datos del diagrama adjunto:

>	eqDAT:=[h5l=400e3*J_/kg_,h3=920e3*J_/kg_,h6=950e3*J_/kg_,h1=1060e3*J_/kg_,h2=1040e3*J_/kg_]:evalf(%,3);'x5'=x5_;x5__:=subs(eqDAT,x5_):'x5'=evalf(%,3);

i.e. licúa un 5,5%

f) Fracción que debe ser derivada hacia el expansor para conseguir las condiciones expuestas en e).

Sea lambda la fracción derivada. Con T7=T0 por la aproximaci\363n dicha en el enunciado:

>	eqBE_HX:=(1-lambda)*(h2-h3)=((1-lambda)*x5+lambda)*(h7-h6);lambda_:=solve(%,lambda):lambda__:=subs(h2=c[p]*T2,h3=c[p]*T3,h6=c[p]*T6,h7=c[p]*T7,T7=T0,T6=T6_,x5=x5__,dat,lambda_):'lambda[MGP]'=evalf(%,2);lambda___:=subs(h7=h1,eqDAT,x5=x5__,lambda_):'lambda[DAT]'=evalf(%,2);

i.e. habría que derivar un 13%, según los datos del diagrama (el modelo de gas perfecto da un 5%).

g) Potencia real consumida.

>

Wnet:=Wmp-Wexp;Wcomp:=mcomp*wisot;Wexp:=mexp*(h2-h6);eqBM_L:=ml=mcomp*(1-lambda)*(1-x5);mcomp_:=subs(x5=x5__,lambda=lambda___,dat,solve(%,mcomp)):'mcomp'=evalf(%,2);Wcomp_:=subs(dat,mcomp_*wisot_):'Wcomp'=evalf(%,2);mexp:='lambda*mcomp';mexp_:=lambda___*mcomp_:'mexp'=evalf(%,2);Wexp_:=subs(eqDAT,dat,mexp_*(h2-h6)):'Wexp'=evalf(%,2);Wnet_:=Wcomp_-Wexp_:'Wnet'=evalf(%,2);;

i.e., incluso con la aproximación isoterma, ya se consumirían 23 kW frente a los 2,5 kW del límite termodinámico.

>