>	restart:#"m18_p03"

Se desea enfriar una corriente fluida desde T1 a T2 (sin cambio de fase) en dos escalones. Con un refrigerador, R1, se enfriará hasta Ti (intermedia entre T1 y T2) y con otro, desde Ti hasta T2. Se pide:
a) Ti óptima suponiendo que ambas máquinas R1 y R2 son de Carnot.
b) Ti óptima suponiendo que las máquinas tienen rendimiento proporcional al de Carnot.
c) Ti óptima suponiendo máquinas de Carnot endo reversibles con transmisión de calor proporcional al salto de temperatura en las fuentes.
d) ¿Cuál sería el coste energético mínimo usando infinitas máquinas de Carnot?
e) Hacer aplicación para 1 kg/s de aire desde 16 ºC hasta -25 ºC.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):assume(m>0,c[p]>0,T1>0,T2>0,T>0):

>	su1:="Aire":dat:=[m=1*kg_/s_,T1=(15+273)*K_,T2=(-25+273)*K_];

>

>

>

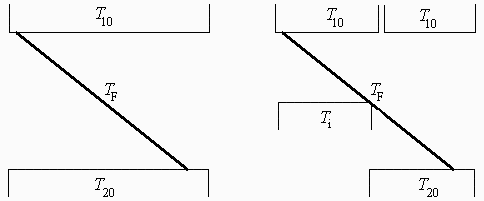
Esquema:

Eqs. const.:

>	dat:=op(dat),get_gas_data(su1),Const,SI2,SI1:

a) Ti óptima suponiendo que ambas máquinas R1 y R2 son de Carnot.

Suponemos que la temperatura de partida es la temperatura ambiente.

Para enfriar una corriente fluida desde T1 a T2 (sin cambio de fase) hay que quitarle una energía:

>	Q2:=m*c[p]*(T1-T2);Q2_:=subs(dat,%);

i.e. unos 40 kW que, si se utilizase una única fuente térmica, como habría de operar como mínimo entre T1 y T2, consumiría un trabajo mínimo (proporcional a las temperaturas absolutas, según Carnot):

>	Wmin:='Q2*(T1-T2)/T2';Wmin_:=subs(dat,%);

i.e. unos 6,5 kW, con un rendimiento de refrigeración de 6,2 (cada kW rinde 6,2 kW):

>	eta[R]:='Q2/W';eta[R,Carnot]:=T2/(T1-T2);eta[R,Carnot]:=evalf(subs(dat,%));

Si se usan 2 máquinas, sin embargo, una puede trabajar ebtre T1 y una Tintermedia, mientras que la otra deberá trabajar entre T1 y T2, pues si lo hiciera entre esa Tintermedia y T2 el conjunto sería idéntico a una sóla máquina.

La primera máquina sólo puede enfriar hasta Tintermedia, luego:

>	Qi:=m*c[p]*(T1-Ti);WminM1:='Qi*(T1-Ti)/Ti';

mientras que para la segunda máquina:

>	WminM2:='(Q2-Qi)*(T1-T2)/T2';

Luego el trabajo mínimo total es:

>	Wmin:='WminM1+WminM2';'Wmin'=Wmin;eqmin:=Diff('Wmin',Ti)=0;eqmin_:=diff(Wmin,Ti)=0;Ti_Wmin:=solve(%,Ti)[1];Ti_Wmin_:=evalf(subs(dat,%));Wmin_:=evalf(subs(Ti=Ti_Wmin,dat,SI0,Wmin))*W_;

Se deduce que la Tintermedia óptima es la media geométrica de las temperaturas extremas, 267 K, y que el trabajo mínimo se reduce de 6,5 kW a 4,7 kW.

b) Ti óptima suponiendo que las máquinas tienen rendimiento proporcional al de Carnot.

>	WminM1:='(Qi*(T1-Ti)/Ti)/alpha1';WminM2:='((Q2-Qi)*(T1-T2)/T2)/alpha2';Wmin:='WminM1+WminM2';'Wmin'=Wmin;eqmin:=Diff('Wmin',Ti)=0;eqmin_:=diff(Wmin,Ti)=0;Ti_Wmin:=solve(%,Ti)[2];

Puede comprobarse que si los coeficientes de proporcionalidad son iguales, se recupera el resultado anterior para la Ti.

>	assume(alpha>0):Ti_Wmin_alpha:=simplify(subs(alpha1=alpha,alpha2=alpha,Ti_Wmin));Wmin_:=evalf(subs(alpha1=alpha,alpha2=alpha,alpha=0.5,Ti=Ti_Wmin_alpha,dat,SI0,Wmin))*W_;

e.g. si las máquinas sólo dan el 50%de las de Carnot, en vez de 4,7 kW harían falta 9,5 kW.

c) Ti óptima suponiendo máquinas de Carnot endo reversibles con transmisión de calor proporcional al salto de temperatura en las fuentes.

Sea Ti la que alcanza el fluido tras la primera máquina, habiendo evacuado Qi=mc(T1-Ti), pero ahora la primera máquina trabajará entre T11>T1 y Ti1<Ti tal que Qi=Ki(Ti-Ti1) y (Qi+WminM1=K1(T11-T1).

Para la Máquina1:

>	Qi:=m*c[p]*(T1-Ti);eqHTi:='Qi'=Ki*(Ti-Ti1);WM1:='Qi*(T11-Ti1)/Ti1';eqHT1:='Qi+WM1'=K1*(T11-T1);Ti1_:=solve(eqHTi,Ti1);T11_:=solve(subs(Ti1=Ti1_,eqHT1),T11);WM1_:=subs(Ti1=Ti1_,T11=T11_,WM1);

Puede comprobarse que en el límite de gran transmitancia térmica se recupera el primer caso.

>	WM1_Kgrande:=convert(series(subs(Ki=1/iKi,convert(series(subs(K1=1/iK1,WM1_),iK1,1),polynom)),iKi,2),polynom);

Para la Máquina2:

>	T11_:='T11_':Qi2:=m*c[p]*(Ti-T2);eqHT2:='Qi2'=K2*(T2-T21);WM2:='Qi2*(T11_-T21)/T21';eqHT1:='Qi2+WM2'=K1_*(T11_-T1);T21_:=solve(eqHT2,T21);T11__:=solve(subs(T21=T21_,eqHT1),T11_);WM2_:=subs(T21=T21_,T11_=T11__,WM2);

Puede comprobarse que en el límite de gran transmitancia térmica se recupera el primer caso.

>	WM2_Kgrandes:=convert(asympt(convert(asympt(WM2_,K2,2),polynom),K1_,1),polynom);

El valor de Ti que minimiza el trabajo total es:

>	Wt:='WM1+WM2';Wt_:=WM1_+WM2_:eqmin:=Diff('Wt',Ti)=0;#eqmin_:=diff(Wt_,Ti)=0;Ti_Wtmin:=solve(%,Ti)[1];

Bueno, se hace así, pero no queda una expresión sencilla.

d) ¿Cuál sería el coste energético mínimo usando infinitas máquinas de Carnot?
Sea un proceso de enfriamiento infinitesimal desde T hasta T-dT, con una máquina de Carnot genérica, que trabajará entre T y T1.

>	eta:=dQ/dW;eta:=T/(T1-T);dQ:=-m*c[p]*dT;W12:=Int(1,W);W12:=Int((T1-T)/T,Q);W12:=Int(-m*c[p]*(T1-T)/T,T=T1..T2);W12_:=collect(value(%),{m,c[p]});W12__:=evalf(subs(dat,SI0,%))*W_;

i.e. el coste energético con infinitas máquinas de Carnot sería de 3 kW. Puede comprobarse con coincide con la exergía de la corriente:

>	Dpsi:=Dh-T0*Ds;Wmin:=m*(c[p]*(T2-T1)-T0*c[p]*ln(T2/T1));Wmin_:=subs(dat,evalf(subs(dat,%)));

Resulta interesante comparar el rendimiento frigorífico global éste, con el de una sola máquina de Carnot, que era de 6,2.

>	eta[R,Carnot,infinity]:='Q12/W12';eta[R,Carnot,infinity]:=Q2_/Wmin_;

que muestra que la eficiencia con infinitas máquinas sería mayor; si la diferencia de temperaturas no es grande, el rendimiento sería el doble.

>	eq:=eta[R,Carnot]/eta[R,Carnot,infinity]='Wmin[infinity]/Wmin';eq:=eta[R,Carnot]/eta[R,Carnot,infinity]=(m*c[p]*(T1-T2)/(T2/(T1-T2)))/Wmin;eq_:=simplify(subs(T0=T1,T2=T1*(1-delta),%));lhs(%)=convert(series(rhs(%),delta=0,4),polynom);

>