Considérese una planta de potencia nuclear de 50 kW eléctricos para un futuro sistema de propulsión espacial. Se trata de un ciclo Brayton cerrado, con CO2 como fluido de trabajo, el cual entra a 10 MPa y 500 K al compresor (C), saliendo a 20 MPa y pasando luego por un recuperador de calor (HX) donde alcanza 1000 K antes de entrar al reactor nuclear (RN), de donde sale a 1200 K para entrar en la turbina (T). Después el gas pasa a contracorriente por el intercambiador de calor HX, y finalmente por un radiador (R) donde se enfría hasta los 500 K antes de entrar al compresor. Tomando para los rendimientos isoentrópicos de compresor y turbina un valor de 0,85, despreciando la caída de presión en los cambiadores, y con unos valores medios para el CO2 como gas ideal en todo el proceso de cp=1250 J/(kg·K) y =1,20, se pide:
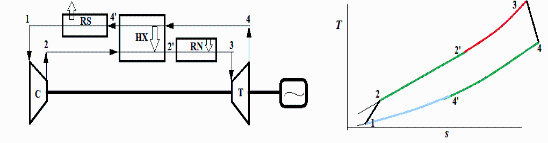
a) Esquema de la instalación, y diagrama T-s del proceso.
b) Temperatura a la salida del compresor, y trabajo unitario necesario.
c) Temperatura a la salida de la turbina, y trabajo unitario.
d) Gasto másico de gas necesario.
e) Potencia térmica del reactor nuclear.
Datos:
| > |
read`../therm_chem.m`:with(therm_chem):with(therm_proc): |
| > |
su1:="CO2":dat:=[Wele=50e3*W_,T2p=1000*K_,T3=1200*K_,p2=20e6*Pa_,p1=10e6*Pa_,T1=500*K_,eta[C]=0.85,eta[T]=0.85,c[p]=1250*J_/(kg_*K_),gamma=1.20,M=0.044*kg_/mol_];dat:=op(dat),Const,SI2,SI1: |
a) Esquema de la instalación, y diagrama T-s del proceso.
b) Temperatura a la salida del compresor, y trabajo unitario necesario.
| > |
eq5_59;eq5_61;T2_:=subs(dat,rhs(%));wC=c[p]*(T2-T1);wC_:=subs(dat,c[p]*(T2_-T1)); |
i.e. del compresor sale a 572 K, necesitando un trabajo de 90 kJ/kg.
c) Temperatura a la salida de la turbina, y trabajo unitario.
| > |
eq5_60;eq5_62;p4=p1;p3=p2;T4_:=subs(p3=p2,p4=p1,dat,rhs(eq5_62));wT=c[p]*(T3-T4);wT_:=subs(dat,c[p]*(T3-T4_)); |
i.e. de la turbina sale a 1090 K, produciendo un trabajo de 139 kJ/kg. Con el modelo de gas ideal, las diferencias de temperatura en el cambiador HX serán iguales por ser el mismo gasto másico, luego si el flujo de alta presión se calienta de T2=572 K hasta T2'=1000 K (DT=428 K), el de baja presión se enfriará desde T4=1089 K hasta T4'=T4-DT=1089-428=661 K, antes de pasar por el radiador y enfriarse hasta los 500 K de entrada al compresor.
d) Gasto másico de gas necesario.
| > |
Wele='m*(wT-wC)';mCO2_:=subs(dat,Wele/(wT_-wC_)) |
i.e. el flujo de gas circulante ha de ser de 1 kg/s.
e) Potencia térmica del reactor nuclear.
| > |
QRN=m*c[p]*(T3-T2p);QRN_:=subs(dat,mCO2_*c[p]*(T3-T2p)); |
i.e. en el RN deben liberarse 255 kW para generar los 50 kW de electricidad, por lo que el rendimiento de esta planta de potencia es de 50/255=20 %, no muy bueno; con otros ciclos de potencia se llega a rendimientos del 40 %, si bien para aplicaciones espaciales pudiera ser competitivo este ciclo, que puede hacerse muy compacto y relativamente ligero, y ahorrar mucho combustible en su puesta en órbita.
Nota. Este problema está inspirado en una propuesta de Sondelski-2019, donde calculan que la masa total (radiador, recuperador, reactor nuclear, turbomáquinas...) podría ser inferior a 500 kg; también pueden encontrarse muchos otros datos de diseño.

![eta = `/`(`*`(`+`(`^`(pi[12], `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))), `*`(`+`(`/`(`*`(T2), `*`(T1)), `-`(1))))](images/p60_4.gif)
![T2 = `*`(T1, `*`(`+`(1, `/`(`*`(`+`(`^`(`/`(`*`(p2), `*`(p1)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))), `*`(eta[C])))))](images/p60_5.gif)
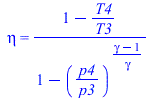
![T4 = `*`(T3, `*`(`+`(1, `-`(`*`(eta[T], `*`(`+`(1, `-`(`^`(`/`(`*`(p4), `*`(p3)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma)))))))))))](images/p60_10.gif)