>	restart:#m17_p48.mw"

Se trata de calcular las pérdidas de exergía en el intercambiador de calor de un ciclo combinado en el que se vaporiza 1 kg/s de agua a 10 MPa que entra a 50 ºC y sale a 500 ºC, lo que se consigue con un flujo a contracorriente de gases de escape que entran al cambiador a 1000 ºC y salen a 100 ºC, todo ello en un ambiente a 25 ºC. Se pide:
a) Calcular la temperatura de vaporización del agua y las variaciones de entalpía y de entropía del agua entre la entrada y la salida.
b) Calcular las variaciones de entalpía y de entropía de los gases entre la entrada y la salida.
c) Generación de entropía en el cambiador, y pérdida de exergía.
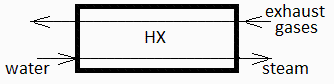
d) En una publicación se dice que la exergía perdida,  , en un cambiador sin cambio de fase es  , siendo   el calor intercambiado, T0 la temperatura ambiente, y Thot and Tcold las temperaturas medias logarítmicas del fluido caliente y del fluido frío, respectivamente; e.g. Thot=(Thot,inThot,out)/ln(Thot,inThot,out). Aplicar la fórmula dada a cada uno de los tres tramos en que puede dividirse el cambiador: calentamiento del agua, ebullición, y sobrecalentamiento, y comparar con el resultado del apartado anterior.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="H2O":su2:="Aire":dat:=[mw=1*kg_/s_,p1=10e6*Pa_,T0=(50+273.15)*K_,T4=(500+273.15)*K_,T1g=(1000+273.15)*K_,T2g=(100+273.15)*K_,p0=100e3*Pa_,T0=(25+273.15)*K_];

Usaremos el modelo de aire estándar para los gases de escape (i.e. gas perfecto con cp=1000 J/(jg·K) constante).

>	datW:=gamma=1.33,get_gas_data(su1),get_liq_data(su1):datG:=get_gas_data("Aire"):dat:=op(dat),SI1,SI2:get_pv_data(su1):

a) Calcular la temperatura de vaporización del agua y las variaciones de entalpía y de entropía del agua entre la entrada y la salida.

Sea 1-2-3-4 los estados del agua, y 2g-1gsegunda-1gprima-1g los correspondientes al gas (que va a contracorriente).

Usaremos el modelo de sustancia perfecta para ambos fluidos, pese a que para el agua 10 MPa es ya casi la mitad de la pcr=22 MPa.

La temperatura de entrada de los gases parece muy alta (1000 ºC), lo que implicaría una relación de presiones muy baja en la turbina de gas.

>

hliq=hl(T);hvap=hv(T);T1_:=subs(dat,T0);p1_:=subs(dat,p1);T2=Tv(p1);h1_:=subs(datW,T=T1_,dat,hl(T));s1_:=subs(dat,evalf(subs(datW,T=T1_,p=p1,dat,sl(T))));T2_:=solve(subs(dat,pv(T)=p1),T);'T2_'=TKC(%);h2_:=subs(datW,T=T2_,dat,hl(T));s2_:=subs(dat,evalf(subs(datW,T=T2_,p=p1,dat,sl(T))));T3_:=T2_;h3_:=subs(datW,T=T3_,dat,hv(T));s3_:=subs(dat,evalf(subs(datW,T=T3_,p=p1,dat,sv(T,p))));T4_:=subs(dat,T4);h4_:=subs(datW,T=T4_,dat,hv(T));s4_:=subs(dat,evalf(subs(datW,T=T4_,p=p1,dat,sv(T,p))));DH=mw*(h4-h1);DH_:=subs(dat,SI1,mw*(h4_-h1_));DS=mw*(s4-s1);DS_:=subs(dat,SI1,mw*(s4_-s1_));

i.e. a 10 MPa el agua hierve a 583 K (310 ºC), y el proceso global desde 50 ºC hasta 500 ºC tiene un salto de entalpía de 3,3 MW (este es el calor que recibe el agua), y un salto de entropía de 6 kW/K.

b) Calcular las variaciones de entalpía y de entropía de los gases entre la entrada y la salida.

Hay que determinar primero el flujo de gases involucrado. Las propiedades las aproximaremos por las del aire, aunque la composición de los gases de escape de una turbina de gas suele ser  77%N2+14%O2+4.6%CO2+4.6%H2O+0.04%NOx. Tampoco corregiremos por temperatura, pese a que a 1000 ºC es cp=1200 J/(kg·K) en vez de 1000 J/(kg·K) y convendría tomar un valor intermedio.

>	eqmg:=mg=mw*(h4-h1)/(c[p]*(T1g-T2g));eqmg_:=subs(h1=h1_,h4=h4_,datG,dat,%);DHg=mg*c[p]*(T1g-T2g);DHg_=subs(eqmg_,datG,dat,SI1,mg*c[p]*(T1g-T2g));DSg:=mg*(c[p]*ln(T1g/T2g)-R*ln(p1g/p2g));DSg_:=subs(SI1,evalf(subs(p2g=p0,p1g=p0,eqmg_,datG,dat,DSg)));

i.e. han de circular 3,6 kg/s de gases, y su variación de entalpía será igual a la del agua porque estamos despreciando las pérdidas de calor al ambiente en el cambiador. Su variación de entropía es de 4,5 kW/K que pierde el gas (el agua ganaba 6 kW/K, y por tanto la Sgen del universo se comprueba que es positiva: 6-4,5=1,5 kW/K.

c) Generación de entropía en el cambiador, y pérdida de exergía.

Como es globalmente adiabático, la pérdida de exergía (irreversibilidad, I) será I=T0·Sgen.

>	Sgen='DSw-WSg';Sgen_:=DS_-DSg_;Psi[lost]=T[0]*S[gen];Psi_lost:=subs(dat,SI1,T0*Sgen_);

i.e. la generación de entropía en el cambiador es de 1,5 kW/K, y la pérdida de exergía de 500 kW (i.e. además de vaporizar el agua con los 3,23 MW antedichos, podría haberse producido una potencia mecánica de casi 0,5 MW, tomando energía del ambiente y con otros procesos, claro que esto es un límite termodinámico inalcanzable).

d) En una publicación se dice que la exergía perdida,  , en un cambiador sin cambio de fase es  , siendo   el calor intercambiado, T0 la temperatura ambiente, y Thot and Tcold las temperaturas medias logarítmicas del fluido caliente y del fluido frío, respectivamente; e.g. Thot=(Thot,inThot,out)/ln(Thot,inThot,out). Aplicar la fórmula dada a cada uno de los tres tramos en que puede dividirse el cambiador: calentamiento del agua, ebullición, y sobrecalentamiento, y comparar con el resultado del apartado anterior.

Esta fórmula se puede deducir a partir de la expresión general d=dhT0ds.

Sea un elemento diferencial de longitud del cambiador en la que el fluido frío recibe un calor dQcold, que será igual, en valor absoluto, al que cede el caliente).

>	eq0:=dSgen=dScold-dShot;eq0:=dSgen=dQcold/Tcold-dQhot/Thot;eq1:=dQcold=m[cold]*c[p,cold]*dT[cold];eq01:=dScold=m[cold]*c[p,cold]*dT[cold]/T[cold];

Integrando, y recordando que DHcold=- DHhot:

>

eq01:=DScold=m[cold]*c[p,cold]*ln(T[cold,output]/T[cold,input]);eq01:=DScold=DH[cold]*ln(T[cold,output]/T[cold,input])/(T[cold,output]-T[cold,input]);eq01:=DScold=DH[cold]/T[LMTDcold];Psi[lost]=(DH[cold]+DH[hot])-T[0]*(DS[cold]+DS[hot]);Psi[lost]=-T[0]*(DS[cold]+DS[hot]);Psi[lost]=-T[0]*(DH[cold]/T[LMTDcold]+DH[hot]/T[LMTDhot]);Psi[lost]=-Q*(T[0]/T[LMTDcold]+T[0]/T[LMTDhot]);

como se quería demostrar.

Para aplicar la fórmula dada a cada uno de los tres tramos en que puede dividirse el cambiador (calentamiento del agua, ebullición, y sobrecalentamiento) calculemos primero las temperaturas intermedias del gas:

>	eqBE1:=mg*c[p]*(T1g-T1pg)=mw*(h4-h3);T1pg_:=subs(eqmg_,datG,dat,T1g-mw*(h4_-h3_)/(mg*c[p]));eqBE3:=mg*c[p]*(T1sg-T2g)=mw*(h2-h1);T1sg_:=subs(eqmg_,datG,dat,T2g+mw*(h2_-h1_)/(mg*c[p]));

Tramo 1 (agua líquida de T1 a T2, gases bajando de T1segundag a T2g).

>

eqSgen1:=Sgen1='Q1*(1/Tm1-1/Tm1g)';Q1:=mw*(h2-h1);Q1_:=subs(dat,SI1,mw*(h2_-h1_));Tm1=(T2-T1)/ln(T2/T1);Tm1_:=(T2_-T1_)/ln(T2_/T1_);'Tm1_'=TKC(%);Tm1g=(T1sg-T2g)/ln(T1sg/T2g);Tm1g_:=evalf(subs(dat,(T1sg_-T2g)/ln(T1sg_/T2g)));'Tm1g_'=TKC(%);Sgen1:=Q1_*(1/Tm1_-1/Tm1g_);Psi[lost1]=subs(dat,SI1,T0*Sgen1);

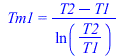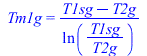i.e. en este trama 1 se intercambian Q1=1,1 MW, generándose Sgen1=326 W/K, perdiéndose 105 kW de exergía.

Tramo 2 (cambio de fase).. Es un caso particular en el que, al no variar la T, LMTD=T.

>	eqSgen2:=Sgen2='Q2*(1/Tm2-1/Tm2g)';Q2:=mw*(h3-h2);Q2_:=subs(dat,SI1,mw*(h3_-h2_));Tm2=T2;Tm2_:=T2_;'Tm2_'=TKC(%);Tm2g=(T1pg-T2sg)/ln(T1pg/T1sg);Tm2g_:=subs(dat,(T1pg_-T1sg_)/ln(T1pg_/T1sg_));'Tm2g_'=TKC(%);Sgen2:=Q2_*(1/Tm2_-1/Tm2g_);Psi[lost2]=subs(dat,SI1,T0*Sgen2);

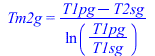i.e. en este trama 2 se intercambian Q2=1,8 MW, generándose Sgen2=1085 W/K, perdiéndose 351 kW de exergía.

Tramo 3 (vapor sobrecalentado de T3 a T4, con gases bajando de T1g a T1primag).

>	eqSgen3:=Sgen3='Q3*(1/Tm3-1/Tm3g)';Q3:=mw*(h4-h3);Q3_:=subs(dat,SI1,mw*(h4_-h3_));Tm4=(T4-T3)/ln(T4/T3);Tm3_:=(T4_-T3_)/ln(T4_/T3_);'Tm3_'=TKC(%);Tm3g=(T1g-T1pg)/ln(T1g/T1pg);Tm3g_:=subs(dat,(T1g-T1pg_)/ln(T1g/T1pg_));'Tm3g_'=TKC(%);Sgen3:=Q3_*(1/Tm3_-1/Tm3g_);Psi[lost3]=subs(dat,SI1,T0*Sgen3);

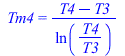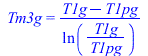i.e. en este trama 1 se intercambian Q3=0,4 MW, generándose Sgen3=260 W/K, perdiéndose 84 kW de exergía.

Conclusión:

-Calor. En el primer tramo se intercambian 1,1 MW, en el segundo 1,8 MW, y en el tercero 0,4 MW, que en total suman los 3,23 MW.

-Sgen. En el primer tramo se crean 326 W/K de entropía, en el segundo 1085 W/K, y en el tercero 260 kW, que en total suman 1670 W/K. Este valor es algo mayor que el obtenido directamente en el apartado c), Sgen=1530 W/K por el modelo de sustancia pura usado para el agua, como se explica a continuación.

-Wlost. En el primer tramo se pierden 105 kW de exergía, en el segundo 350 kW, y en el tercero 84 kW, que en total suman 540 kW. Este valor es algo mayor que el obtenido directamente en el apartado c), 496 kW por la razón anterior.

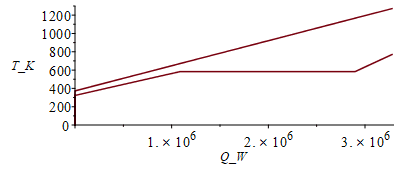
La representación temperatura / calor intercambiado a lo largo del cambiador es:

plot(subs(dat,SI0,[[Q1_+Q2_+Q3_,T1g],[0,T2g],[0,0],[0,T1_],[Q1_,T2_],[Q1_+Q2_,T2_],[Q1_+Q2_+Q3_,T4_]]),Q_W=0..3.3e6,T_K=0..1300);

NOTA. Discrepancia en el cálculo de la entropía de vaporización a 10 MPa con el modelo de sustancia perfecta.

Los valores exactos (datos NIST) son Tv)311 ºC, hLV=1317 kJ/kg, y sLV=2255 J/(kg·K).

Por un lado la hemos calculado como:

>	sLV=sv3-sv2;sLV_:=subs(SI1,s3_-s2_);

Pero para el cálculo con la temperatura media la hemos puesto como:

>	sLV=hLV/Tv;sLV=(h3-h2)/T2;sLV_:=subs(SI1,(h3_-h2_)/T2_);

por lo cual, aunque ya sabíamos que este modelo de sustancia perfecta se desviaba mucho cerca del punto crítico, resulta que también introduce una incongruencia en el propio modelo cuando se usan expresiones distintas para el cálculo de Ds aun con el mismo modelo.

>