>	restart:#"m17_p51"

Se piensa aprovechar los gases de escape de un motor diésel para producir una potencia mecánica adicional usando un ciclo Rankine transcrítico de CO2. El escape suministra 1 kg/s de gases a 200 ºC. El CO2 se toma del condensador saturado a 27 ºC y se comprime hasta 20 MPa con una bomba; luego  recibe calor de los gases de escape hasta llegar a 150 ºC y se expande en una turbina, de la que pasa al condensador, cerrándose el ciclo. Suponiendo despreciable la generación de entropía en la bomba y la turbina, y que el ambiente está a 20 ºC y 95 kPa, se pide:

a) Potencia mecánica máxima recuperable de los gases de escape (aproximar como aire puro).

b) Evolución del CO2 en el diagrama p-h.

c) Gasto de CO2 circulante.

d) Potencia mecánica producida, y rendimiento del ciclo.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(RealDomain):

>	su1:="CO2":su2:="Aire":dat:=[mG=1*kg_/s_,TG=(200+273.15)*K_,T1=(27+273.15)*K_,T3=(150+273.15)*K_,T0=(20+273.15)*K_,p0=95e3*Pa_];

>	Cdat:=get_gas_data(su1),get_liq_data(su1):get_pv_data(su1):Adat:=get_gas_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Potencia mecánica máxima recuperable de los gases de escape (aproximar los gases como aire puro).

La exergía termomecánica del flujo de gases de escape es:

>	WGmax:=mG*(psi[G]-psi[0]);psi:=h-T0*s;Dh:=c[p]*(TG-T0);Ds:=c[p]*ln(TG/T0)-R*ln(pG/p0);WGmax_:=subs(dat,evalf(subs(pG=p0,Adat,dat,mG*(Dh-T0*Ds))));

i.e. el máximo trabajo útil obtenible sería 40 kW (límite termodinámico, inalcanzable). Nótese que la presión no influye.

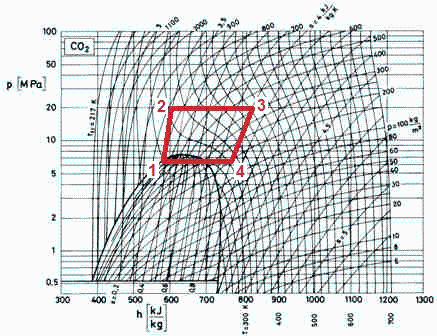
b) Evolución del CO2 en el diagrama p-h.

No es aplicable el modelo de sustancia perfecta por ser transcrítico. Usamos el diagrama p-h del CO2.

El estado 1 (salida del condensador y entrada a la bomba) es líquido saturado a 27 ºC, y le corresponde p1=6,7 MPa (gráfico o ecuación de Antoine). Del gráfico: h1=580 kJ/kg, y s1=3,4 kJ/(kg·K).

El estado 2 se obtiene en el gráfico por intersección de la s1 con la p2=20 MPa, resultando h2=600 kJ/kg y T2=325=52 ºC.

El estado 3 es p3=p2=20 MPa y T3=150 ºC=423 K, resultando h3=820 kJ/kg y s3=4.0 kJ/(kg·K).

El estado 4 se obtiene en el gráfico por intersección de la s3 con la p1=6.7 MPa, resultando h4=760 kJ/kg (T4=320 K=47 ºC)..

>	[pcr,Tcr]=subs(Cdat,[p[cr],T[cr]]);p1:=p[v](T1);p1_:=subs(dat,evalf(subs(dat,pv(T1))));h1:=580e3*J_/kg_;h2:=600e3*J_/kg_;h3:=820e3*J_/kg_;h4:=760e3*J_/kg_;

c) Gasto de CO2 circulante.

Suponiendo adiabático el cambiador de calor, y para el caso límite de que los gases se enfriaran hasta la temperatura de entrada del CO2 al cambiador:

>	eqBEcal:=QG=QC;eqBEcal:='mG*c[p]*(TG-TGout)=mC*(h3-h2)';TGout=T2;TGout:=322*K_;'TGout'=TKC(%);mC_:=subs(Adat,dat,solve(eqBEcal,mC));Q_:=subs(dat,mC_*(h3-h2));

i.e. hay que hacer circular 0,69 kg/s de CO2 para recoger los 152 kW de calor..

d) Potencia mecánica producida, y rendimiento del ciclo.

>	eqW:=W=WT-WB;eqWT:=WT='mC*(h3-h4)';WT_:=subs(mC=mC_,dat,rhs(%));eqWB:=WB='mC*(h2-h1)';WB_:=subs(mC=mC_,dat,rhs(%));W_:=WT_-WB_;eqeta:=eta=W/Q;eqeta_:=subs(W=W_,Q=Q_,eqeta);

i.e. se generarían 28 kW (frente al límite de 40 kW), con un rendimiento energético del 18%; el rendimiento exergético es 28/40=0,7. Nótese que la bomba consume una parte apreciable del trabajo de la turbina.

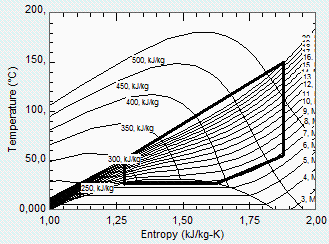
Con los datos del NIST, en kJ/kg (pero con ota referencia): h1=284, h2=302 (50,8 ºC), h3=523,2, h4=467,5 (55,5 ºC), así que Q=149 kW, mC=0,675 kg/s, W=37.6-12.1= 25,5 kW, con eta=17%. Las discrepancias se deben a la incertidumbre en la apreciación de valores en el gráfico usado. El proceso en el diagrama T-s (uniendo los puntos por rectas) es:

>

>