>	restart:#"m17_p50"

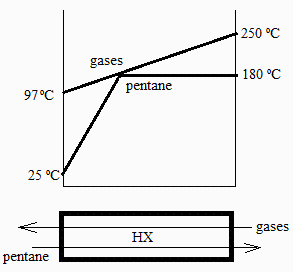
Se necesita una potencia mecánica de 10 kW, y se quiere estudiar la posibilidad de conseguirlo usando un ciclo Rankine de n-pentano, entrando a la turbina vapor saturado a 180 ºC. Como fuente de calor se piensa usar un flujo de gases de escape de un motor a 250 ºC, y el aire ambiente puede tomarse a 25 ºC y 100 kPa. Se pide:

a) Determinar la entalpía y la entropía a la entrada de la turbina, respecto al estado líquido en el punto triple, con el modelo de sustancia perfecta.

b) Determinar la entalpía y la entropía del vapor de pentano saturado a 25 ºC, y las condiciones a la salida de la turbina, suponiendo un rendimiento isoentrópico 0,8.

c) Calcular el gasto másico de pentano necesario y el rendimiento del ciclo.

d) Calcular el gasto másico necesario de gases de escape.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):Digits:=5:with(plots):

>	su1:="C5H12":su2:="Aire":dat:=[Wdot=10e3*W_,T3=(180+273.15)*K_,TG=(250+273.15)*K_,T0=(25+273.15)*K_,eta[T]=0.8];

>	Fdat:=get_gas_data(su1),get_liq_data(su1):get_pv_data(su1):ptr_:=subs(dat,evalf(subs(Fdat,pv(T[f])))):Tm_ptr_Tb_Tcr_pcr:=subs(Fdat,[T[f],ptr_,T[b],T[cr],p[cr]]);Adat:=get_gas_data(su2):dat:=op(dat),Fdat,Const,SI2,SI1:

a) Determinar la entalpía y la entropía a la entrada de la turbina, respecto al estado líquido en el punto triple, con el modelo de sustancia perfecta

>	eqhv:=hv=hv(T);eqsv:=sv=sv(T,p);p3=p[v](T3);p3_:=subs(dat,evalf(subs(dat,pv(T3))));eqh3:=h3=subs(dat,T=T3,dat,hv(T));eqs3:=s3=subs(dat,evalf(subs(dat,T=T3,p=p3_,dat,sv(T,p))));

i.e. h3=960 kJ/kg y s3=3,1 kJ/(kg·K).

El punto triple lo hemos aproximado como Ttr=Tfusion y ptr=pv(Ttr) con los coeficientes de Antoine; los datos más precisos para el n-pentano son Ttr=143,45 K y ptr=0,076 Pa, y p3=2,610 MPa..

El NIST-REFPRO usa como referencia el líquido en su punto de ebullición normal, y los valores correspondientes de h3 y s3 son 563 kJ/kg y 1.40 kJ/(kg·K), respectivamente.

b) Determinar la entalpía y la entropía del vapor de pentano saturado a 25 ºC, y las condiciones a la salida de la turbina, suponiendo un rendimiento isoentrópico 0,8.

Supondremos que la máxima expansión posible es hasta la pv(T0), i.e. desde 2,6 MPa hasta 68 kPa, y que es toda en fase gaseosa.

>

T0=subs(dat,T0);p4v=p[v](T0);p4v_:=subs(dat,evalf(subs(dat,pv(T0))));eqh4v:=h4v=subs(dat,T=T0,dat,hv(T));eqs4v:=s4v=subs(dat,evalf(subs(dat,T=T0,p=p4v_,dat,sv(T,p))));eqT:=eta[T]=(1-T4/T3)/(1-(p4/p3)^((gamma-1)/gamma));T4:=T3*(1-eta[T]*(1-(p4/p3)^((gamma-1)/gamma)));gamma=subs(Fdat,gamma);T4_:=subs(p3=p3_,p4=p4v_,dat,T4);p4_:=p4v_;

i.e. h4v=700 kJ/kg y s4v=2,8 kJ/(kg·K). Nótese que s4v<s3 indica que la expansión es toda en zona gaseosa.

c) Calcular el gasto másico de pentano necesario y el rendimiento del ciclo.

Supondremos que la máxima expansión posible es hasta la pv(T0), i.e. desde 2,6 MPa hasta 68 kPa.

>	eqh4:=h4=subs(dat,T=T4_,dat,hv(T));eqBE:=Wdot=mdot*(h3-h4);mdot_:=subs(eqh3,eqh4,dat,solve(eqBE,mdot));eqh1:=h1=subs(dat,T=T0,dat,hl(T));eqh2:=h2=h1;Qdot:=mdot*(h3-h2);Qdot_:=subs(mdot=mdot_,eqh3,eqh2,eqh1,dat,Qdot);eqeta:=eta='Wdot/Qdot';subs(dat,eta=Wdot/Qdot_);

i.e. hay que procesar como mínimo 0,074 kg/s de pentano, y el rendimiento energético del motor es del 22%.

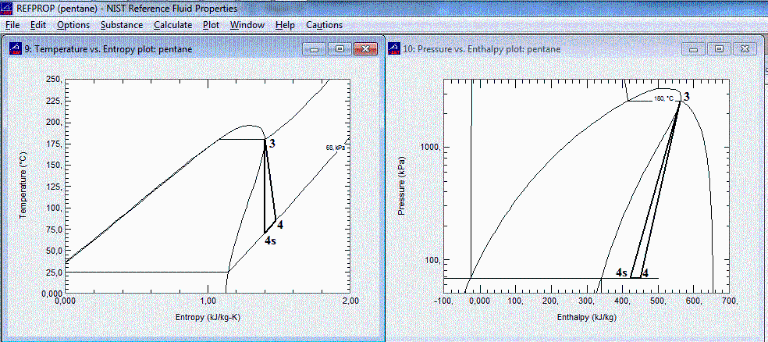
Con los datos del NIST: p3=2,61 MPa, h3=563,2 kJ/kg, s3=1,40 kJ/(kg·K), p4v=68,3 kPa, h4v=340,4 kJ/kg, s4v=1,14 kJ/(kg·K). Nótese que no se ha usado la misma referencia (aquí, líquido en ebullición).

El 4s (expansión isentrópica) da T4s=344 K y h4s=422,7 kJ/kg, y el punto 4 queda (h4=450,8 kJ/kg) a T4=359 K. El gasto mínimo resulta mdot=0,089 kg/s.

d) Calcular el gasto másico necesario de gases de escape.

Los gases de escape entrarán al cambiador de calor a 250 ºC y contracorriente (que es lo mejor), pero su temperatura de salida estará limitada por el acercamiento máximo, que tendrá lugar en el punto 3l (líquido saturado a 180 ºC). Aun suponiendo que en ese punto el acercamiento fuese total (DT=0), y tomando para los gases de escape cp=cp_aire (aunque será algo mayor por tener mucho vapor de agua y CO2), tendremos

>

eqh3l:=h3l=subs(dat,T=T3,dat,hl(T));Qdot_vap:=mdot*(h3-h3l);Qdot_vap_:=subs(eqh3,eqh3l,dat,mdot_*(h3-h3l));Qdot_liq:=mdot*(h3l-h2);Qdot_liq_:=subs(eqh3l,eqh2,eqh1,dat,mdot_*(h3l-h1));eqBEHXpitch:=mdotG*cpG*(TG-(T3+DT))='Qdot_vap';DT:=0;mdotG_:=subs(Adat,dat,Qdot_vap_/(c[p]*(TG-T3)));eqBEHX:=mdotG*cpG*(TG-TGe)='Qdot';TGe_:=subs(Adat,dat,TG-Qdot_/(mdotG_*c[p]));'TGe'=TKC(%);

i.e., de los 46 kW que recibe el pentano, 25 kW son para calentar el líquido tras la bomba y 21 kW para vaporizarlo, necesitándose como mínimo 0,3 kg/s de gases de escape, los cuales saldrían a 97 ºC.

>