>	restart;#"m17_p38"

En una publicación se lee que una central de ciclo combinado Brayton-Rankine genera 9 MW con la turbina de gas y 2 MW con la de vapor, entrando los gases a la turbina de gas a 1,5 MPa y 1200 ºC, y a la turbina de vapor a 4 MPa y 400 ºC. Se pide:
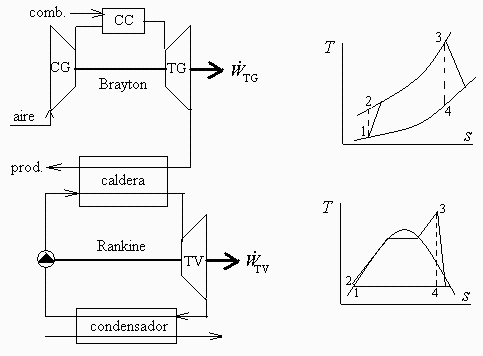
a) Esquema de componentes y diagrama T-s de los procesos.
b) Gasto másico de vapor producido.
c) Gasto másico de aire.
d) ¿Es necesario quemar combustible adicional en la caldera?

e) ¿Y si se considera un rendimiento isentrópica del 85% para el compresor y las turbinas, y una expansión del vapor hasta 3,6 kPa?
Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="H2O":su2:="Aire":dat:=[WTG=9e6*W_,WTV=2e6*W_,p2g=1.5e6*Pa_,T3g=(1200+273)*K_,p3v=4e6*Pa_,T3v=(400+273)*K_,p4v=3.6e3*Pa_,eta=0.85];

>	Adat:=get_gas_data(su2):Wdat:=gamma=1.33,get_gas_data(su1),get_liq_data(su1):dat:=op(dat),Wdat,Const,SI2,SI1:get_pv_data(su1):

a) Esquema de componentes y diagrama T-s de los procesos.

Como no se dan rendimientos, supondremos las expansiones y compresiones isentrópicas.

b) Gasto másico de vapor producido.

Suponiendo rendimiento ideal para la turbina de vapor, y descarga máxima, i.e. a la pv(T0).

>	wTV:=h3-h4;h3_:=subs(dat,T=T3v,dat,hv(T));T3_:=subs(dat,T3v);p3_:=subs(dat,p3v);p4_:=subs(dat,evalf(subs(dat,pv(T0))));wet_vap(T3_,p3_,p4_);h4=h4s;wTV_:=h3_-h4s_;eqmTV:=m=WTV/wTV;eqmTV_:=subs(wTV=wTV_,dat,%);

En la práctica nunca se hace trabajar a la turbina con tan baja fracción másica de vapor (77%), pero las condiciones de entrada sí son usuales, por lo que el problema está en las suposiciones: en la realidad, un rendimiento isentrópico típico de un 85% (en vez del 100%) y una expansión típica hasta 5 kPa (en vez de a 1,7 kPa), corregirían la x4.

Por otra parte, el gasto de vapor hallado es el mínimo, pues supone rendimiento máximo; en la práctica será un 15% o 20% mayor.

c) Gasto másico de aire.

Supondremos rendimiento ideal para la turbina de gas y el compresor.

>	wTG:=c[p]*(T3-T4-T2+T1);T4:=T3g*(p0/p2g)^((gamma-1)/gamma);'gamma'=subs(Adat,gamma);T4_:=subs(Adat,dat,T4);T2:=T0*(p2g/p0)^((gamma-1)/gamma);T2_:=subs(Adat,dat,%);T1:=T0;wTG_:=subs(T3=T3g,Adat,dat,wTG);eqmTG:=m='WTG/wTG';eqmTG_:=subs(T3=T3g,wTG=wTG_,Adat,dat,%);

Ese es el gasto mínimo, correspondiente al rendimiento máximo de las máquinas. En la práctica, con rendimientos isentrópicos del orden del 85%, se requeriría bastante más aire, del orden del 30% al 40% más.

d) ¿Es necesario quemar combustible adicional en la caldera?

Lo primero que habrá que comprobar es que la temperatura de salida de la TG es superior a la de entrada a la TV.

Lo segundo que habrá que comprobar es que el calor que cede el aire es suficiente para generar el vapor.

>	eqScald:=T4g>T3v;eqScald_:=T4_>subs(dat,T3v);is(subs(SI0,%));eqBEcald:=mv*(h3v-h2v)<ma*c[p]*(T4g-T5);T5:=Tv_p3v;T5_:=subs(dat,evalf(solve(subs(dat,p3v)=pv(T),T)));h2_:=subs(dat,T=T0,dat,hl(T));eqBEcald_:=subs(eqmTV_,dat,m*(h3_-h2_))<subs(eqmTG_,Adat,dat,m*c[p]*(T4_-T5_));is(subs(SI0,%));

Con las suposiciones idealizadas, el 'aire' saldría a 679 K y a duras penas podría calentar el vapor hasta 673 K, pero en la práctica el gas saldría más caliente y no habría este problema.

Con las suposiciones idealizadas, el 'aire' no sería capaz de generar ese vapor si sólo es capaz de enfriarse hasta esa T5. Hay que estudiar en más detalle los perfiles de temperatura en la caldera.

Sobrecalentamiento. Para sobrecalentar 1,54 kg/s de vapor desde los 522 K de vaporización hasta los 673 K de entrada a la turbina, la temperatura de los gases debe bajar desde los 679 K de la salida de la turbina de gas hasta:

>	T5_1:='T4'-(T3v-T5)*mv*cv/(ma*ca);T5_1_:=T4_-subs(dat,T3v-T5_)*subs(eqmTV_,Wdat,m*c[p])/subs(eqmTG_,Adat,m*c[p]);

Luego, para vaporizar 1,54 kg/s de vapor a 522 K, la temperatura de los gases debe bajar desde los 656 K hasta:

>	T5_2:='T5_1'-h[lv,Tv]*mv/ma;hlvT5_:=subs(Wdat,T=T5_,dat,hlv(T));T5_2_:=T5_1_-hlvT5_*subs(eqmTV_,m)/subs(eqmTG_,Adat,m*c[p]);

que ya no es posible porque 507 K < 522 K.

Conclusión, con el modelo asumido (de rendimientos isentrópicos ideales) no es posible hacer funcionar el ciclo combinado sin aportar más energía del exterior (e.g. añadiendo más fuel y un combustor en la caldera). Pero antes, habría que modelizar mejor este problema, no vaya a ser que al tener en cuenta unos rendimientos realistas sí que sea suficiente con el recuperador de calor de gases de escape.

Si rehacemos el problema añadiendo rendimientos isentrópicos del 85%, y una presión de condensación más realista p4v=3,6 kPa, tenemos:

a) Esquema de componentes y diagrama T-s de los procesos.
b) Gasto másico de vapor producido.

>

wTV:=h3-h4;h3_:=subs(dat,T=T3v,dat,hv(T));T3_:=subs(dat,T3v);p3_:=subs(dat,p3v);p4_:=subs(dat,p4v);T4v_:=subs(dat,evalf(subs(dat,solve(p4v=pv(T),T))));wet_vap(T3_,p3_,p4_);eqeta:=eta=(h3-h4)/(h3-h4s);h4_:=subs(dat,h3_-eta*(h3_-h4s_));x4:=(h4-h4l)/(h4v-h4l);h4l_:=subs(dat,T=T4_,dat,hl(T));h4v_:=subs(dat,T=T4_,dat,hv(T));x4_:=(h4_-h4l_)/(h4v_-h4l_);wTV_:=h3_-h4_;eqmTV:=m=WTV/wTV;eqmTV_:=subs(wTV=wTV_,dat,%);

i.e. se necesitan 1.9 kg/s de vapor y no 1,5 kg/s.

c) Gasto másico de aire.

Supondremos rendimiento ideal para la turbina de gas y el compresor.

>

T4:='T4':T2:='T2':wTG:=c[p]*(T3-T4-T2+T1);T1:=T0;pi[12]=subs(dat,p2g/p0);dat:=op([dat]),%:eq5_59;T2_:=subs(T1=T0,solve(%,T2));T2__:=subs(Adat,dat,%);subs(p4=p3/pi[12],eq5_60);T4_:=solve(%,T4);T4__:=subs(T3=T3g,Adat,dat,%);wTG_:=subs(T1=T0,T2=T2__,T3=T3g,T4=T4__,Adat,dat,wTG);eqmTG:=m='WTG/wTG';eqmTG_:=subs(T1=T0,T2=T2__,T3=T3g,T4=T4__,wTG=wTG_,Adat,dat,%);

>

i.e. 32 kg/s en vez de 20 kg/s.

d) ¿Es necesario quemar combustible adicional en la caldera?

Lo primero que habrá que comprobar es que la temperatura de salida de la TG es superior a la de entrada a la TV.

Lo segundo que habrá que comprobar es que el calor que cede el aire es suficiente para generar el vapor.

>	eqScald:=T4g>T3v;eqScald_:=T4__>subs(dat,T3v);is(subs(SI0,%));eqBEcald:=mv*(h3v-h2v)<ma*c[p]*(T4g-T5);T5:=Tv_p3v;T5_:=subs(dat,evalf(solve(subs(dat,p3v)=pv(T),T)));h2_:=subs(dat,T=T4v_,dat,hl(T));eqBEcald_:=subs(eqmTV_,dat,m*(h3_-h2_))<subs(eqmTG_,Adat,dat,m*c[p]*(T4__-T5_));is(subs(SI0,%));

Efectivamente, si se tienen en cuenta los rendimientos isentrópicos, al procesarse bastante más aire en la turbina y salir los gases de escape más calientes, sobra luego calor en la caldera para generar todo el vapor necesario (pese a haber aumentado la cantidad necesaria de éste)..

>