>	restart:#"m17_p18"

En el reactor de una central nuclear de agua a presión se calienta ésta a 15 MPa hasta 300 °C, pasando luego a una cámara de expansión a 5 MPa. La parte de vapor que se produce en la expansión brusca en la cámara se hace pasar por una turbina de rendimiento adiabático 0,85 donde se expande hasta 10 kPa, pasando posteriormente por un condensador y una bomba que introduce el condensado en una cámara de mezcla a 5 MPa, a la que también se lleva la fracción que quedó líquida en la cámara de expansión. Desde allí se bombea todo el agua a 15 MPa hacia el reactor, completándose el ciclo. Se pide:

a) Esquema de la instalación y diagrama T s del proceso.

b) Exergía del agua a la salida del reactor, respecto de una atmósfera a 100 kPa y 288 K.

c) Fracción másica de vapor producida en la cámara de expansión.

d) Trabajo generado en la turbina, por unidad de gasto circulante por el reactor.

e) Temperatura de entrada del agua al reactor.

f) Rendimiento energético de la central.

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="H2O":dat:=[p1=15e6*Pa_,T1=(300+273)*K_,p2=5e6*Pa_,eta[T]=0.85,p4=10e3*Pa_];

Ec. de balance y const.:

>	eqBE:=eq5_43;gdat:=get_gas_data(su):ldat:=get_liq_data(su):get_pv_data(su):dat:=op(dat),gamma=1.33,gdat,ldat,Const,SI2,SI1:

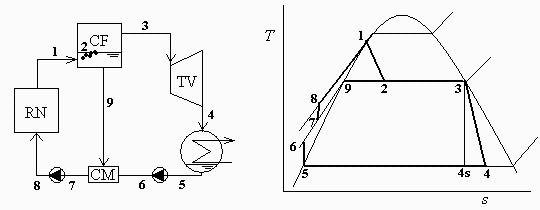
a) Esquema de la instalación y diagrama T s del proceso.
(Arriba.)

b) Exergía del agua a la salida del reactor, respecto de una atmósfera a 100 kPa y 288 K

Como los estados inicial y final son líquidos, con el modelo de sustancia perfecta (al final comprobaremos su validez), la exergía de pasar una corriente en condiciones 0 a condiciones 1 será:

>	psi:=Dh-T0*Ds;Dh:=c*(T1-T0);Ds:=c*ln(T1/T0);Dh_:=subs(dat,Dh):'Dh'=evalf(%,2);Ds_:=subs(dat,Ds):'Ds'=evalf(%,2);psi_:=subs(dat,evalf(subs(dat,psi))):'psi'=evalf(%,2);

i.e. el agua sale con una exergía de 360 kJ/kg.

c) Fracción másica de vapor producida en la cámara de expansión.

>

Tvp1_:=subs(dat,evalf(subs(dat,solve(p1=pv(T),T)))):Tvp1=evalf(%,3);Tvp1=TKC(Tvp1_);Tvp2_:=subs(dat,evalf(subs(dat,solve(p2=pv(T),T)))):Tvp2=evalf(%,3);Tvp2=TKC(Tvp2_);Tvp4_:=subs(dat,evalf(subs(dat,solve(p4=pv(T),T)))):Tvp4=evalf(%,3);Tvp4=TKC(Tvp4_);h=hv(T);h1_:=subs(dat,T=T1,dat,hl(T)):h1=evalf(%,2);h9_:=subs(dat,T=Tvp2_,dat,hl(T)):h9=evalf(%,2);h3_:=subs(dat,T=Tvp2_,dat,hv(T)):h3=evalf(%,2);eqBE_CF:=h1=x2*h3+(1-x2)*h9;x2=solve(%,x2);x2_:=(h1_-h9_)/(h3_-h9_):'x2'=evalf(%,2);

i.e. se vaporiza el 8 %.

d) Trabajo generado en la turbina, por unidad de gasto circulante por el reactor.

>

eqBE_TV:=w=x2*(h3-h4);s3_:=subs(dat,evalf(subs(dat,T=Tvp2_,p=p2,dat,sv(T,p)))):s3=evalf(%,2);s4v_:=subs(dat,evalf(subs(dat,T=Tvp4_,p=p4,dat,sv(T,p)))):s4v=evalf(%,2);s5_:=subs(dat,evalf(subs(dat,T=Tvp4_,p=p4,dat,sl(T,p)))):s5=evalf(%,2);x4s=(s3-s5)/(s4v-s5);x4s_:=(s3_-s5_)/(s4v_-s5_):x4s=evalf(%,2);h4s=(1-x4s)*h5+x4s*h4v;h5_:=subs(dat,T=Tvp4_,dat,hl(T)):h5=evalf(%,2);h4v_:=subs(dat,T=Tvp4_,dat,hv(T)):h4v=evalf(%,2);h4s_:=(1-x4s_)*h5_+x4s_*h4v_:h4s=evalf(%,2);eqetaT:=eta[T]=(h3-h4)/(h3-h4s);h4_:=subs(dat,h3_-eta[T]*(h3_-h4s_)):h4=evalf(%,2);x4=(h4-s5)/(h4v-h5);x4_:=(h4_-h5_)/(h4v_-h5_):x4=evalf(%,2);eqBE_TV:=w=x2_*(h3_-h4_):evalf(%,2);

i.e. la salida de la turbina es con un 82 % de masa de vapor, y genera 71 kJ/kg.

e) Temperatura de entrada del agua al reactor.

Despreciando las contribuciones energéticas de las bombas:

>	eqBE_CM:=h8=(1-x2)*h9+x2*h5;eqBE_CM_:=h8=(1-x2_)*h9_+x2_*h5_:evalf(%,2);T8_:=subs(eqBE_CM_,dat,T[tr]+h8/c):T8=evalf(%,3);T8=TKC(T8_);;

i.e. el agua entra a 245 ºC.

f) Rendimiento energético de la central.

Despreciando el trabajo de bombeo:

>	eqeta:=eta='w/(h1-h8)';eqeta_:=eta=subs(eqBE_TV,eqBE_CM_,w/(h1_-h8)):evalf(%,2);

i.e. el rendimiento es del 31 %.
Hemos resuelto el problema con el modelo de sustancia perfecta, con el que rho=cte=1000 kg/m3 para el agua, pero las variaciones de temperatura son grandes y en realidad, usando los datos más exactos:

Estado 1:

>

dat1:=[T=573*K_,p=15e6*Pa_,h=1.338e6*J_/kg_,s=3230*J_/(kg_*K_),rho=710*kg_/m_^3];dat2:=[T=537*K_,p=5e6*Pa_,h=1.338e6*J_/kg_,s=3260*J_/(kg_*K_),x=0.11];dat3:=[T=537*K_,p=5e6*Pa_,h=2.794e6*J_/kg_,s=5970*J_/(kg_*K_)];dat9:=[T=537*K_,p=5e6*Pa_,h=1.154e6*J_/kg_,s=2920*J_/(kg_*K_),x=0,rho=770*kg_/m_^3];dat4:=[T=319*K_,p=1e4*Pa_,h=2.025e6*J_/kg_,s=6400*J_/(kg_*K_),x4=0.77,x4s=0.71];dat5:=[T=319*K_,p=1e4*Pa_,h=0.192e6*J_/kg_,s=650*J_/(kg_*K_),x=0,rho=990*kg_/m_^3];dat0:=[T=293*K_,p=610*Pa_,h=-0.04e6*J_/kg_,s=-0.2*J_/(kg_*K_)];eqBE_CM:=h8=(1-x2)*h9+x2*h5;eqBE_CM_:=subs(x2=x,dat2,h9=h,dat9,h5=h,dat5,eqBE_CM):evalf(%,2);

>	psi:='psi':eq1:=psi=(h1-h0)-T0*(s1-s0);eq1_:=subs(h1=h,s1=s,dat1,h0=h,s0=s,dat0,dat,eq1):evalf(%,2);w:='w':eq2:=w=x2*(h3-h4);eq2_:=subs(x2=x,dat2,h3=h,dat3,h4=h,dat4,eq2):evalf(%,2);eq3:=eta=w/(h1-h8);eq3_:=subs(eq2_,h1=h,dat1,eqBE_CM_,eq3):evalf(%,2);

i.e. la exergía es 450 kJ/kg en vez de 360 kJ/kg, el trabajo unitario es 85 kJ/kg en vez de 71 kJ/kg, y el rendimiento es del 29% en vez del 31%.

>