>	restart:#"m17_p09"

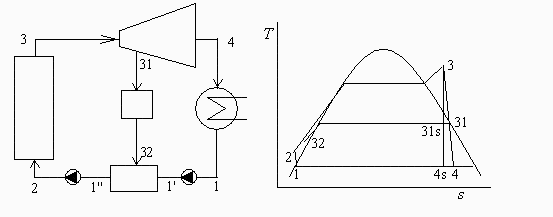
La entrada a una turbina de vapor es a 1,5 MPa y 250 ºC. A 250 kPa se extrae parte del vapor para suministrar 5 MW a una carga térmica, de donde retorna el condensador a 200 kPa y 85 ºC, entrando a través de una válvula a un tanque de recogida a presión atmosférica. La salida de la turbina al condensador se hace a 5 kPa, enfriándose el agua hasta 30 ºC, tras de lo cual es bombeada al tanque de recogida, desde el cual se bombea hasta la caldera. La eficiencia adiabática de las bombas y de la turbina puede tomarse igual a 0,7. Sabiendo que las condiciones atmosféricas son 92 kPa y 20 ºC, y que la potencia neta obtenida es 4 MW, calcular el flujo de agua necesario y la eficiencia global del proceso.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="H2O":dat:=[T3=(250+273.15)*K_,p3=1.5e6*Pa_,p31=250e3*Pa_,QdotCT=5e6*W_,p32=200e3*Pa_,T32=(85+273.15)*K_,p4=5e3*Pa_,T41=(30+273.15)*K_,eta[t]=0.7,eta[b]=0.7,p0=92e3*Pa_,T0=(20+273)*K_,Wdot=4e6*W_];

Ec. balance y constitutivas.

>	eqBE:=eq5_43;Wgdat:=get_gas_data(su1):Wldat:=get_liq_data(su1):get_pv_data(su1):dat:=op(dat),gamma=1.33,Wgdat,Wldat,Const,SI2,SI1:

a) Calcular el flujo de agua necesario y la eficiencia global del proceso.

Primero calculamos el gasto de vapor que necesita la carga térmica:

>

eq1:=QdotCT=mCT*(h31-h32);h32_:=evalf(subs(dat,T=T32,dat,hl(T))):'h32'=evalf(%/(1e3*J_/kJ_),3);T31s=T31vp31;T31s_:=fsolve(subs(dat,SI0,subs(dat,p31)=pv(T)))*K_:'T31s'=evalf(%,3);'T31s'=TKC(T31s_);h3_:=subs(dat,T=T3,p=p3,dat,hv(T,p)):'h3'=evalf(%/(1e6*J_/MJ_),3);wet_vap(subs(dat,T3),subs(dat,p3),subs(dat,p31));x31s_:=x4s_:'x31s'=evalf(%,2);h31s_:=h4s_:'h31s'=evalf(%/(1e6*J_/MJ_),3);h31=h3*(1-eta[t])+eta[t]*h31s;h31_:=evalf(subs(dat,h3_*(1-eta[t])+eta[t]*h31s_)):'h31'=evalf(%/(1e6*J_/MJ_),3);x31:=(h31-h31l)/(h31v-h31l);h31l_:=subs(dat,T=T31s_,dat,hl(T)):'h31l'=evalf(%,2);h31v_:=subs(dat,T=T31s_,dat,hv(T)):'h31v'=evalf(%,2);x31_:=(h31_-h31l_)/(h31v_-h31l_):'x31'=evalf(%,2);mCT_:=subs(dat,h32=h32_,h31=h31_,dat,solve(eq1,mCT)):'mCT'=evalf(%,2);

i.e. se necesita 2,1 kg/s de vapor para la CT, que se cogen de un punto intermedio de la turbina prácticamente saturado (31).

Ahora veamos cuánto vapor se necesita para generar el trabajo dicho.

>

eq2:=Wdot=mdot*(h3-h31)+(mdot-mCT)*(h31-h4);T4s_:=subs(dat,evalf(subs(dat,solve(p4=pv(T),T)))):'T4s'=evalf(%,3);'T4s'=TKC(T4s_);wet_vap(subs(dat,T3),subs(dat,p3),subs(dat,p4));'h4s'=evalf(h4s_/(1e6*J_/MJ_),2);h4=h3*(1-eta[t])+eta[t]*h4s;h4_:=evalf(subs(dat,h3_*(1-eta[t])+eta[t]*h4s_)):'h4'=evalf(%/(1e6*J_/MJ_),3);x4:=(h4-h4l)/(h4v-h4l);h4l_:=subs(dat,T=T4s_,dat,hl(T)):'h4l'=evalf(%,2);h4v_:=subs(dat,T=T4s_,dat,hv(T)):'h4v'=evalf(%,2);x4_:=(h4_-h4l_)/(h4v_-h4l_):'x4'=evalf(%,2);eq2_:=subs(dat,h3=h3_,h31=h31_,h4=h4_,eq2):mdot_:=subs(mCT=mCT_,dat,solve(eq2_,mdot)):'mdot'=evalf(%,2);

i.e. a la caldera han de entrar 7,5 kg/s de agua.

Nótese la ligera discrepancia entre el valor de la temperatura de condensación correspondiente a la presión dada, 32,8 ºC, y el valor de la temperatura que se cita en el enunciado, 30 ºC; demasiada discrepancia para ser atribuible a la incertidumbre en la medida o a la caida de presión en el condensador.

El rendimiento global se puede definir de varias maneras: como (Wdot+QdotCT)/Qcald, como (Wdot+QdotCT*eta)/Qcald, o como (Wdot+QdotCT*etaCT)/(Qcald*etacald); la 1ª no es recomendable porque equipara el trabajo y el calor, cuyo coste es diferente.

>

eq3:=eta[e]=(Wdot+QdotCT*(1-T0/T3))/Qcald;Qcald:=mdot*(h3-h2);eqBEXH:=(mdot-mCT)*h1+mCT*h32=mdot*h2;h1:=h4l;h1_:=h4l_:'h1'=evalf(%,2);h2_:=h1_+(mCT_/mdot_)*(h32_-h1_):'h2'=evalf(%,2);Qcald_:=subs(dat,mdot_*(h3_-h2_)):'Qcald'=evalf(%,2);eq3:=eta[e]=subs(dat,(Wdot+QdotCT*(1-T0/T3))/Qcald_):evalf(%,2);

i.e. el combustible en la caldera debe dar 21 MW, y el rendimiento energético normalizado es del 30%, que es bastante bajo debido al poco sobrecalentamiento (a 1,5 MPa hierve a 200 ºC y sólo se sobrecalienta hasta 250 ºC).

>	pvT3_:=subs(dat,evalf(subs(dat,pv(T3)))):'pvT3'=evalf(%,2);Tvp3_:=subs(dat,evalf(subs(dat,solve(p3=pv(T),T)))):'Tvp3'=evalf(%,3);'Tvp3'=TKC(Tvp3_);

Podemos comparar ese modelo de sustancia perfecta con los valores de tablas:

>

h3__:=2923e3*J_/kg_;h32__:=356e3*J_/kg_;h31s__:=2579e3*J_/kg_;h31__:=evalf(subs(dat,h3__*(1-eta[t])+eta[t]*h31s__)):'h31'=evalf(%/(1e6*J_/MJ_),3);mCT_:=subs(dat,h32=h32__,h31=h31__,dat,solve(eq1,mCT)):'mCT'=evalf(%,2);h4s__:=2045e3*J_/kg_;h4__:=evalf(subs(dat,h3__*(1-eta[t])+eta[t]*h4s__)):'h4'=evalf(%/(1e6*J_/MJ_),3);eq2_:=subs(dat,h3=h3__,h31=h31__,h4=h4__,eq2):mdot_:=subs(mCT=mCT_,dat,solve(eq2_,mdot)):'mdot'=evalf(%,2);

i.e. el modelo sencillo es suficiente.

>