>	restart:#"m17_p03"

Se trata del aprovechamiento de un manantial geotérmico (agua caliente subterránea) de 20 m3/h de agua a presión y a 130 °C, para generar electricidad utilizando el agua como foco térmico en una máquina de Rankine cuyo fluido de trabajo es n-butano, y que opera entre 0,3 MPa y 1,8 MPa, entrando a la turbina vapor saturado. Se pide:

a) Potencia eléctrica máxima producible (límite termodinámico).

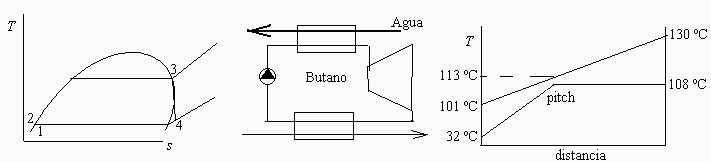
b) Esquema de la instalación propuesta y diagrama T s del proceso.

c) Temperaturas extremas del fluido de trabajo.

d) Trabajo específico de la turbina.

e) Gasto másico necesario de butano

f) Potencia generada.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="H2O":su2:="C4H10":dat:=[V=(20/3600)*m_^3/s_,Tw=(130+273)*K_,p1=0.3e6*Pa_,p3=1.8e6*Pa_,eta[T]=1];

>

>	eqBE:=eq5_43;Wdat:=get_liq_data(su1):gdat:=get_gas_data(su2):ldat:=get_liq_data(su2):get_pv_data(su2):p[v,nbut](T)=pv(T);dat:=op(dat),gdat,ldat,Const,SI2,SI1:

a) Potencia eléctrica máxima producible (límite termodinámico).

Será la exergía de la corriente de agua respecto al ambiente. Sólo se considera la exergía termomecánica, psi=h-T0·s, despreciando la exergía obtenible del agua en condiciones ambiente respecto a la atmósfera de referencia (dependería de la humedad ambiente, y no sería difícil obtener algo de esa exergía por enfriamiento evaporativo).

Como datos de las sustancias podrían usarse diagramas (p-h, h-s...), tabulaciones..., pero vamos a usar el modelo de sustancia perfecta, comparando con los valores más exactos del NIST (DATA).

>

Wmax:=m*(Dh-T0*Ds);m:=rho*V;rho=subs(Wdat,rho);mw_:=subs(Wdat,dat,rho*V);rho[DATA]:=937.2*kg_/m_^3;m[DATA]:=evalf(subs(dat,rho[DATA]*V),3);Dh:=c*(Tw-T0);Dh_:=subs(Wdat,dat,Dh):'Dh'=evalf(%,2);Ds:=c*ln(Tw/T0);Ds_:=evalf(subs(Wdat,dat,Ds)):'Ds'=evalf(%,2);Wmax_:=subs(dat,evalf(subs(dat,mw_*(Dh_-T0*Ds_)))):'Wmax'=evalf(%,2);WmaxDATA_:=subs(SI0,evalf(m[DATA]*((546000-63000)-288*(1635-225))))*W_:'WmaxDATA'=evalf(%,2);

i.e. el máximo obtenible es 0,42 MW (con los datos del NIST 0,40 MW).

b) Esquema de la instalación propuesta y diagrama T s del proceso.

(Hecho arriba)

c) Temperaturas extremas del fluido de trabajo.

Serán las de cambio de fase a las presiones dadas, pues no hay sobrecalentamiento.

>	Tvp1_:=fsolve(subs(dat,SI0,pv(T)=p1),T=300..700)*K_;Tvp3_:=fsolve(subs(dat,SI0,pv(T)=p3),T=300..700)*K_;Tvp1=TKC(Tvp1_);Tvp3=TKC(Tvp3_);

i.e. el n-butano se vaporizará a 108 ºC y condensará a 32 ºC (con datos del NIST, a 108,7 ºC y 32,4 ºC).

d) Trabajo específico de la turbina.

Como la entrada a la turbina es vapor saturado, se podría suponer salida bifásica (como ocurriría en un ciclo de vapor de agua), pero las moléculas grandes presentan retroceso en la línea de vapor saturado:

>	wet_vap(Tvp3_,subs(dat,p3),subs(dat,p1));

luego sale todo vapor (y no mezcla bifásica). En función del rendimiento isoentrópico de la turbina:

>

eq5_60;T4_:=solve(eq5_60,T4);eta=subs(dat,eta[T]);'gamma'=subs(dat,gamma);T4_:=subs(T3=Tvp3_,eta=eta[T],pi[12]=p3/p1,dat,T4_);'T4'=TKC(T4_);h1_:=subs(dat,T=Tvp1_,dat,hl(T));h2=h1;h3_:=subs(dat,T=Tvp3_,dat,hv(T));h4_:=subs(dat,T=T4_,dat,hv(T));q23=h3-h2;q23_:=h3_-h1_;w34=h3-h4;w34_:=h3_-h4_;eta[e]=w34/q23;eta[e]=evalf(w34_/q23_);

Con datos del NIST:

>	h1data:=276.5e3;h3data:=730.5e3;h4data:=656.2e3;q23data:=h3data-h1data;w34data:=h3data-h4data;eta=evalf(w34data/q23data);

La  discrepancia es apreciable (del orden del 20%) y en contra.

Nótese que el valor de las entalpías depende mucho del estado de referencia elegido: en el modelo de sustancia perfecta hemos tomado h=0 para el líquido en el punto triple, mientras que los datos del NIST estaban referidos al estándar IIR (International Institute of Refrigeration, que toma h=200 kJ/kg para el líquido saturado a 0 ºC).

e) Gasto másico necesario de butano.

Hay que calentar el butano desde Tvp1 a Tvp2 y vaporizarlo a Tvp2, todo ello con una corriente finita de agua que entra a Tw y no se sabe a qué T sale. Dejando un salto mínimo DT=5 ºC (extremo o 'pitch', ver dibujo), sería Tpitch=Tvp3+DT y en aproximación lineal Tsale=Tw-(Tw-Tpitch)*(h3-h1)/(h3-hpitch).

>

eqBECC:=mb*(h3-h2)=mw*c*(Tw-Tsale);DT_:=5*K_;Tpitch=Tvp3+DT;Tpitch_:=Tvp3_+DT_;Tpitch=TKC(Tpitch_);Tsale=Tw-(Tw-Tpitch)*(h3-h1)/(h3-hpitch);hpitch_:=subs(dat,T=Tpitch_,dat,hl(T)):hpitch=evalf(%,2);Tsale_:=subs(dat,Tw-(Tw-Tpitch_)*(h3_-h1_)/(h3_-hpitch_));Tsale=TKC(Tsale_);Q23:=mw*cw*(Tw-Tsale);Q23_:=subs(Wdat,dat,mw_*c*(Tw-Tsale_));mb_:=subs(Wdat,dat,mw_*c*(Tw-Tsale_)/(h3_-h1_));mbDATA_:=subs(Wdat,dat,SI0,m[DATA]*c*(Tw-Tsale_)/(h3data-h1data))*kg_/s_;

i.e. el agua no puede salir más fría de 101 ºC, transmitiendo Q=670 kW de calor al ciclo, por el que ha de circular 1,5 kg/s de n-butano (1.4 kg/s con datos NIST).

f) Potencia generada

>	W34:=mb*(h3-h4);W34_:=subs(dat,mb_*(h3_-h4_));WDATA_:=evalf(subs(dat,mbDATA_*w34data));eta='W34/Q23';eta=W34_/Q23_;

i.e. con este ciclo se generarían 0,13 MW de trabajo en vez del límite termodinámico de 0,42 MW (con datos NIST, 0,10 MW y 0,40 MW, respectivamente).

Como comprobación hemos vuelto a calcular el rendimiento energético del ciclo.

Nótese la mejora que supone en todos estos ciclos ORC (Organic Rankine Cycle) la introducción de un regenerador que aproveche la entalpía del vapor de 4 a 4v, para calentar un poco el líquido de 1 a 1' (ver Fig. 2).

>