>	restart:#"m17_p02"

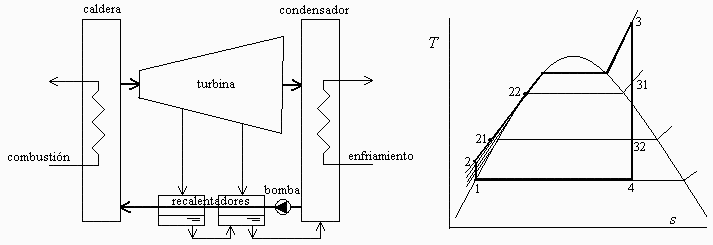
En una central térmica sin recalentamiento y con dos extracciones, la entrada a la turbina es a 650 °C y 8 MPa, con las extracciones a 500 kPa y 70 kPa y salida a 5 kPa. Sabiendo que los calentadores del agua condensada son de tipo cerrado, descargando uno en otro y éste en el condensador a través de sendas válvulas, y que calientan el agua hasta la temperatura de condensación del vapor, calcular el rendimiento energético y las fracciones de sangrado adecuadas.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="H2O":dat:=[T3=(650+273)*K_,p3=8e6*Pa_,p31=500e3*Pa_,p32=70e3*Pa_,p4=5e3*Pa_,eta[T]=1];

Eqs. const.:

>	eqBE:=eq5_43;gdat:=get_gas_data(su1):ldat:=get_liq_data(su1):get_pv_data(su1):dat:=op(dat),gamma=1.33,gdat,ldat,Const,SI2,SI1:

a) Calcular el rendimiento energético y las fracciones de sangrado adecuadas.

Primero calculamos las temperaturas de vapor correspondientes a esas presiones:

>

Tvp3_:=subs(dat,evalf(subs(dat,solve(pv(T)=p3,T)))):'Tvp3_'=evalf(%,3);Tvp31_:=subs(dat,evalf(subs(dat,solve(pv(T)=p31,T)))):'Tvp31_'=evalf(%,3);Tvp32_:=subs(dat,evalf(subs(dat,solve(pv(T)=p32,T)))):'Tvp32_'=evalf(%,3);Tvp4_:=subs(dat,evalf(subs(dat,solve(pv(T)=p4,T)))):'Tvp4_'=evalf(%,3);'Tvp3_'=TKC(Tvp3_);'Tvp31_'=TKC(Tvp31_);'Tvp32_'=TKC(Tvp32_);'Tvp4_'=TKC(Tvp4_);

Segundo, calculamos las temperaturas que corresponderían a esas expansiones si se tratara de un gas perfecto con gamma=1.33):

>	eqS:=T4=T3*(p4/p3)^((gamma-1)/gamma);'gamma'=subs(dat,gamma);T31g_:=subs(p4=p31,dat,rhs(eqS)):T31g=evalf(%,3);T32g_:=subs(p4=p32,dat,rhs(eqS)):T32g=evalf(%,3);T4g_:=subs(dat,rhs(eqS)):T4g=evalf(%,3);T31g=TKC(T31g_);T32g=TKC(T32g_);T4g=TKC(T4g_);

luego sólo el punto 31 es gaseoso (T31g>Tvp31; el 32 y el 4 son bifásicos ya que T32g<Tvp32 y T4g<Tvp4). Las fracciones másicas de vapor serán:

>	x=(h-hl)/(hv-hl);h3_:=subs(dat,T=T3,dat,hv(T)):h3=evalf(%,2);x31_:=1;h31_:=subs(dat,T=T31g_,dat,hv(T)):h31=evalf(%,2);wet_vap(subs(dat,T3),subs(dat,p3),subs(dat,p32)):x32_:=evalf(x4s_,2);h32_:=evalf(h4s_,2);wet_vap(subs(dat,T3),subs(dat,p3),subs(dat,p4)):x4_:=evalf(x4s_,2);h4_:=evalf(h4s_,2);

b) Fracciones de sangrado adecuadas.

>	eqBEC1:='c*(Tvp31_-Tvp32_)=f*(h31_-hl_Tvp31)';f1_:=subs(dat,solve(subs(hl_Tvp31=subs(dat,T=Tvp31_,dat,hl(T)),dat,eqBEC1),f)):f1=evalf(%,2);eqBEC2:='c*(Tvp32_-Tvp4_)=f*(h32_-hl_Tvp32)+f1_*c*(Tvp31_-Tvp32_)';f2_:=subs(dat,solve(subs(hl_Tvp32=subs(dat,T=Tvp32_,dat,hl(T)),dat,eqBEC2),f)):f2=evalf(%,2);

i.e. en el estado 31 hay que extraer un 12 % del caudal, y en el 32 un 9 %.

c) Rendimiento energético.

>	w:='(h3_-h31_)+(1-f1_)*(h31_-h32_)+(1-f1_-f2_)*(h32_-h4_)';w_:=w:'w'=evalf(%,2);q=h3-h31liq;q_:=h3_-subs(dat,T=Tvp31_,dat,hl(T)):q=evalf(%,2);eta='w/q';etae_:=w_/q_:eta=evalf(%,2);

i.e. un 47 %. Pueden compararse los valores calculados con este modelo de sustancia perfecta con los valores tabulados, para ver que la diferencia no es significativa.

>	h3data:=3761.4e3*J_/kg_;s3data:=7153.5*J_/(kg_*K_);T31data:=(221.6+273)*K_;h31data:=2900.9e3*J_/kg_;T32data:=(90+273)*K_;h32data:=2541.4e3*J_/kg_;x32data:=0.9482;T4data:=(32.9+273)*K_;h4:=2181.2e3*J_/kg_;x4:=0.8434;

luego, el modelo aproximado es bueno.

>