| > | restart:#"m17_p01" |
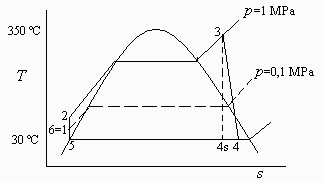
Con una bomba y la caldera de una máquina de vapor se pasa el agua de 100 kPa y 30 °C a 1 MPa y 350 °C, entrando el vapor a una turbina de rendimiento isentrópico 0,85 y saliendo después al condensador, que está aspirado por otra bomba, la cual devuelve el agua a 100 kPa y 30 °C. Se pide:
a) Consumo térmico y producción de trabajo por unidad de gasto másico.
b) Rendimiento energético y exergético de la máquina, suponiendo que se trabaja con un foco térmico a la máxima temperatura y un sumidero térmico a la mínima temperatura.
c) Trabajo mínimo necesario (límite termodinámico) para pasar el agua de 100 kPa y 30 °C a 1 MPa y 350 °C, en presencia de una atmósfera a 30 °C, y comparación con la exergía aportada.
d) Trabajo máximo obtenible (límite termodinámico) al pasar de 1 MPa y 350 °C a 100 kPa y 30 °C, y comparación con el trabajo obtenido.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):
su1:="H2O":dat:=[p1=100e3*Pa_,T1=(30+273)*K_,T0=T1,p3=1e6*Pa_,T3=(350+273)*K_,eta[T]=0.85,eta[B]=0.80]; |
Eqs. const.:
| > | eqBE:=eq5_43;gdat:=get_gas_data(su1):ldat:=get_liq_data(su1):get_pv_data(su1):dat:=op(dat),gdat,ldat,Const,SI2,SI1:[c[L],T[b],h[lv0],c[p]]=subs(dat,[c,T[b],h[lv0],c[p]]);
|
a) Consumo térmico y producción de trabajo por unidad de gasto másico.
Se trata de ir aplicando el balance energético a cada elemento de la instalación.
Supondremos un rendimiento isentrópico típico del 80% para las bombas.
Usaremos el modelo de sustancia perfecta (gas perfecto y líquido perfecto), aunque al final comparemos con los valores de las tablas. Referencia: h=0 y s=0 para el líquido en el punto triple (PT).
Proceso 1-2-3:
| > | eqAntoine:=p[v](T)=pv(T);pv30:=subs(dat,evalf(subs(dat,pv(T1))));pv350:=subs(dat,evalf(subs(dat,pv(T3))));Tv1000_:=fsolve(subs(dat,SI0,pv(T)=p3),T=300..700)*K_;Tv1000_C:=TKC(%);T[tr]=subs(dat,T[tr]);p[tr]=subs(dat,p[tr]);h[PT,liq]=0;h[v]=hv(T);h3_:=subs(dat,T=T3,dat,hv(T));s3_:=subs(dat,evalf(subs(dat,T=T3,p=p3,dat,sv(T,p))));h1_:=subs(dat,T=T1,dat,hl(T));s[PT,liq]=0;s[v]=sv(T,p);s1_:=evalf(subs(dat,T=T1,dat,sl(T)));wB12:=(p2-p1)/(rho*eta[B]);wB12_:=subs(dat,(p3-p1)/(rho*eta[B]));q23:=h3-h2;q23_:=h3_-h1_;
|
 = `+`(`*`(0.1e4, `*`(exp(`+`(16.54, `-`(`/`(`*`(3985.), `*`(`+`(`/`(`*`(T), `*`(K_)), `-`(39.00))))))), `*`(Pa_))))], [p[v](T) = `+`(`*`(0.1e4, `*`(exp(`...](images/p01_5.gif) |
i.e., de 1 a 3 se consumen 1,1 kJ/kg de trabajo en la bomba y 3060 kJ/kg de calor en la caldera.
Proceso 3-4:
Hay que ver si el punto 4-isentrópico está dentro o fuera de la 'campana' de estados bifásicos (e.g. comparando su entropía, s4s=s3, con la del vapor saturado a esa presión, sv(p4)).
| > | T3_:=subs(dat,T3);p3_:=subs(dat,p3);T4_:=subs(dat,T1);p4_:=pv30;wet_vap(T3_,p3_,p4_);eta[T]=(h3-h4)/(h3-h4s);h4_:=subs(dat,h3_-(h3_-h4s_)*eta[T]);x4_:=(h4_-h4l_)/(h4v_-h4l_);w34_:=h3_-h4_:'w34_'=evalf(%,2);wB01_:=subs(dat,(p1-p4_)/(rho*eta[B]));
|
i.e., de 3 a 4 se producen 830 kJ/kg de trabajo en la turbina y se consumen 0,1 kJ/kg en la bomba. Aparte está el calor evacuado al ambiente.
b) Rendimiento energético y exergético de la máquina, suponiendo que se trabaja con un foco térmico a la máxima temperatura y un sumidero térmico a la mínima temperatura.
| > | etae:=wneto/qposit;wneto:='w34-wB01-wB12';wneto_:=w34_-wB01_-wB12_;qposit:=q23;etae_:=(w34_-wB01_-wB12_)/q23_;etaC:=(1-T1/T3);etaC_:=evalf(subs(dat,etaC));etax:='etae/etaC';etax_:=etae_/etaC_; |
i.e., el rendimiento energético global es del 27% y el exergético del 52%.
c) Trabajo mínimo necesario (límite termodinámico) para pasar el agua de 100 kPa y 30 °C a 1 MPa y 350 °C, en presencia de una atmósfera a 30 °C, y comparación con la exergía aportada.
| > | wmin13:=h3-h1-T0*(s3-s1);wmin13_:=subs(dat,dat,h3_-h1_-T0*(s3_-s1_));phi13aportada:='wB12+q23*(1-T1/T3)';phi13aportada_:=subs(dat,wB12_+q23_*(1-T1/T3));
|
i.e., de 1 a 3 se ha aportado una exergía de 1600 kJ/kg.
d) Trabajo máximo obtenible (límite termodinámico) al pasar de 1 MPa y 350 °C a 100 kPa y 30 °C, y comparación con el trabajo obtenido.
| > | wmax31:='wmin13';wmax31_:=evalf(wmin13_,2);phi31obtenida:=w34-wB01;phi31obtenida_:=w34_-wB01_;
|
i.e., de 3 a 1 se ha obtenido una exergía de 826 kJ/kg, que, como en todo proceso real, es menor que la aportada en el ciclo (970 kJ/kg), pero más conveniente.
Se pueden comparar los valores con los obtenidos de Tablas más detalladas.
| > | h1data:=125.67e3*J_/kg_;s1data:=436.5*J_/(kg_*K_);h2data:=126.57e3*J_/kg_;h3data:=3.157e6*J_/kg_;q23data:=h3data-h2data:'q23data'=evalf(%,3);s3data:=7300.5*J_/(kg_*K_);h4sdata:=2206.5e3*J_/kg_;x4sdata:=0.8564;w34data:=subs(dat,(h3data-h4sdata)*eta[T]);eta[e]:=w34data/q23data;
|
luego, el modelo aproximado era bueno.
| > |