>	restart:#"m16_p29"

>	read`../therm_chem.m`:with(therm_chem);with(therm_proc):

Se trata de estudiar la composición de equilibrio de los gases de escape en la combustión de gas natural (supóngase metano puro) con aire, sabiendo que la alimentación es con una riqueza de 1,25, y que a la salida, que es a 1800 K, basta considerar las concentraciones de N2, CO2, H2O, CO y H2. En particular, se pide:
a) Plantear el problema, estableciendo las ecuaciones e incógnitas.
b) Determinar el valor de la constante de equilibrio de la reacción del gas de agua.
c) Reducir el problema a una ecuación con una incógnita.
d) Resolver el problema.

Datos:

>	su1:="Aire":su2:="H2O":fuel:=CH4:dat:=[phi=1.25,Ts=1800*K_];

Eqs. const.:

>	Adat:=get_gas_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):dat:=op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:

a) Plantear el problema, estableciendo las ecuaciones e incógnitas.

Nos dan los productos y nos piden sus concentraciones. La ecuación de la mezcla, por unidad de cantidad de sustancia de productos, es:

>	eqMezcla:=eqMIX(a*CH4+b*(c21*O2+c79*N2)=[3,4,6,7,8]);eqNX;eqDat:=a/b=phi/A[0];eqEsteq:=CH4+2*O2=CO2+2*H2O;eqA0:=Ateo(CH4);eqDat_:=subs(A[0]=rhs(eqA0),dat,eqDat);

que nos dan las siguientes ecuaciones de balance másico (o molar) de especies conservativas (átomos):

>	eqBC;eqBH;eqBO;eqBN;

Vemos que nos falta una séptima ecuación para resolver las 7 incógnitas. También la regla de Volterra nos lo enseña: R=C-E=5-4=1. Habrá que plantear una ecuación de equilibrio químico de los productos, y la que normalmente se elige es la del gas de agua:

>	eqEsteq:=CO2+H2=CO+H2O;eqEQ_:=eqEQ(eqEsteq);use RealDomain in ln(lhs(%))=ln(op(1,op(2,%)))+ln(op(2,op(2,%))) end use;

b) Determinar el valor de la constante de equilibrio de la reacción del gas de agua.

>	eqEQ__:=evalf(subs(T=Ts,dat,eqEQ_));

NOTA. Hay que hacer notar que el modelo aproximado usado (lnK=A-B/T) se desvía bastante de los valores experimentales para la reacción del gas de agua. El valor tabulado más preciso de esa K a 1800 K es tan sólo 3,8 en lugar de 10. Pese a ello, la aproximación en la composición de equilibrio es aceptable, como se ve al final.

c) Reducir el problema a una ecuación con una incógnita.

Se pueden despejar 6 incógnitas, en función de la restante, a partir de las 6 ecuaciones lineales, y substituir en la de equilibrio:

>	sol1:=subs(dat,solve({eqNX,eqBC,eqBH,eqBO,eqBN,eqDat_},{a,b,x[N2],x[CO2],x[CO],x[H2O]}));eqEQ___:=subs(sol1,eqEQ__);

d) Resolver el problema.

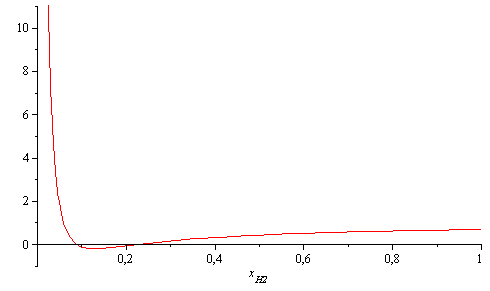
Representando f(x[H2]), o iterando:

>	plot(lhs(eqEQ___),x[H2]=0..1,-1..11);xH2_:=fsolve(eqEQ___,x[H2]=0..0.1);sol1_:=subs(x[H2]=xH2_,sol1);

La solución aquí obtenida, [N2,H2O,CO2,CO,H2]=[67%,20%,4,8%,6,3%,2,6%], no se diferencia mucho de la solución obtenida usando los mejores valores tabulados de la constante de equilibrio, [N2,H2O,CO2,CO,H2]=[67%,18%,6,1%,4,9%,3,9%].

>