>	restart:#"m16_p28"

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):

Se quiere analizar la combustión de una gota de 0,2 mm de diámetro, de n-heptano en aire ambiente, considerando sólo el régimen casi-estacionario tras la ignición. Se pide:
a) Poder calorífico por unidad de masa de combustible.
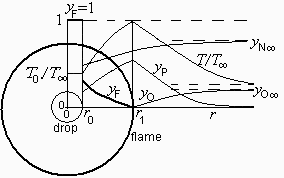
b) Temperatura máxima de llama, y hacer un esquema del perfil de temperaturas esperado.
c) Establecer el balance energético a través de una superficie de radio intermedio entre la gota y la llama.
d) Calcular el tiempo de quemado.

Datos:

>	su1:="Aire":su2:="C7H16":dat:=[D=0.2e-3*m_];

>	Adat:=get_gas_data(su1):Fdat:=get_gas_data(su2),get_liq_data(su2);get_pv_data(su2):dat:=op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:

a) Poder calorífico por unidad de masa de combustible.

>	eq:=eq_fit(C7H16+c1*O2=c2*CO2+c3*H2O);eqA:=Ateo(su2);A0m:=subs(Ma=M,Adat,Mf=M,Fdat,dat,rhs(%)*Ma/Mf);PCS_:=PCS(eq);PCI_:=PCI(eq);PCIm_:=subs(dat,PCI_/rhs(Mf(su2)));

i.e. el poder calorífico inferior es de 45 MJ/kg.

b) Temperatura máxima de llama, y hacer un esquema del perfil de temperaturas esperado.

>	eq_M:=eqMIX(a*C7H16+b*(c21*O2+c79*N2)=[2,3,4,5]);sol1_:=solve(subs(b=rhs(eqA)*a,c=0,d=0,dat,dat,{eqNX,eqBC,eqBH,eqBO,eqBN}),{a,x[Comp[2]],x[Comp[3]],x[Comp[4]],x[Comp[5]]});eq15_7_2;Ta_:=subs(sol1_,cpComp_,dat,T25+a*PCI_/sum(delta[i]*x[Comp[i]]*c[p,Comp[i]],i=1..C_));

i.e. la Tmax alcanzable es de unos 2360 K (será menor por las pérdidas por radiación).

Se puede hacer un diagrama r-t de la variación esperada del radio de la gota con el tiempo, pues se sabe que la combustión de gotas, como la evaporación de gotas, responde a la ley del cuadrado, de Langmuir: r2=r02-Kt, luego:

>	eqr2:=r^2=r[0]^2-K*t;plot({1-t,(1-t)^(1/2),(1-t)^(3/2)},t=0..1,color=black);

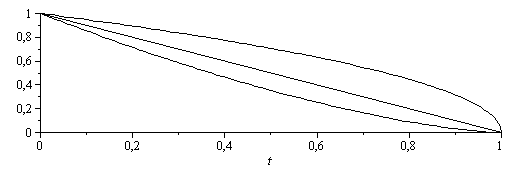c) Establecer el balance energético a través de una superficie de radio intermedio entre la gota y la llama.

>

eqBE:=Acc=Prod+Diff_flux+Conv_flux;eqBE:=0=-mdotF*hlv0+A*k*Diff(T,r)-mdot*c[pF]*(T-T0);eqBE:=0=-hlv0+(k/(rho*v))*Diff(T,r)-c[pF]*(T-T0);eqBE:=dT/(hlv0+c[pF]*(T-T0))=-rho*v*dr/k;eqBE:=ln(1+c[pF]*(Tad-T0)/hlv0)=c[pF]*rho*v0*r0^2*(1/r0-1/r1)/k;eqI:=rho*v0=-rho[liq]*dr0/dt;eqBE:=dr0^2/dt=-(2*k/(rho[liq]*c[pF]))*ln(1+c[pF]*(Tad-T0)/hlv0);

d) Calcular el tiempo de quemado.

>	eqt:=t[q]=(D/2)^2/((2*k/(rho[liq]*c[pF]))*ln(1+c[pF]*(Tad-T0)/h[lv0]));evalf(subs(dat,rho[liq]=rho,c[pF]=c[p],Tad=Ta_,Fdat,dat,%)):evalf(%,2);

i.e. las gotas tardan unos 100 ms en arder, habiendo tomado las propiedades constantes (pese a que la k_aire, e.g. varía de 0.025 W/(m·K) a 300 K a 0.090 W/(m·K) a 1400 K, que sería la temperatura media apropiada.

>