>	restart:#"m16_p27"

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):

Para un estudio de tiempo de quemado de gotas en un motor de gasolina de inyección directa, se quiere analizar la combustión de una gota de 0,1 mm de diámetro, de n-octano en aire ambiente, considerando sólo el régimen casi-estacionario tras la ignición. Se pide:
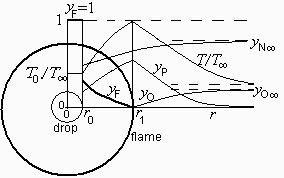
a) Determinar la temperatura máxima de la llama, y hacer un esquema del perfil radial de temperaturas esperado.
b) Hacer un diagrama r-t de la variación esperada del radio de la gota con el tiempo.
c) Establecer el balance energético a través de una superficie de radio intermedio entre la gota y la llama.
d) Calcular el tiempo de quemado.

Datos:

>	su1:="Aire":su2:="C8H18":dat:=[D=0.193e-3*m_];

>	Adat:=get_gas_data(su1):Fdat:=get_gas_data(su2),get_liq_data(su2);get_pv_data(su2):dat:=op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:

a) Determinar la temperatura máxima de la llama, y hacer un esquema del perfil radial de temperaturas esperado.

>

eq:=eq_fit(C8H18+c1*O2=c2*CO2+c3*H2O);eqA:=Ateo(su2);PCI_:=PCI(eq);PCIm_:=subs(dat,PCI_/rhs(Mf(su2)));eq_M:=eqMIX(a*C8H18+b*(c21*O2+c79*N2)=[2,3,4,5]);sol1_:=solve(subs(b=rhs(eqA)*a,c=0,d=0,dat,dat,{eqNX,eqBC,eqBH,eqBO,eqBN}),{a,x[Comp[2]],x[Comp[3]],x[Comp[4]],x[Comp[5]]});eq15_7_2;Ta_:=subs(sol1_,cpComp_,dat,T25+a*PCI_/sum(delta[i]*x[Comp[i]]*c[p,Comp[i]],i=1..C_));

i.e. la Tmax alcanzable es de unos 2400 K (será menor por las pérdidas por radiación).

b) Hacer un diagrama r-t de la variación esperada del radio de la gota con el tiempo.

Se sabe que la combustión de gotas, como la evaporación de gotas, responde a la ley del cuadrado, de Langmuir: r2=r02-Kt, luego:

>	eqr2:=r^2=r[0]^2-K*t;plot({1-t,(1-t)^(1/2),(1-t)^(3/2)},t=0..1,color=black);

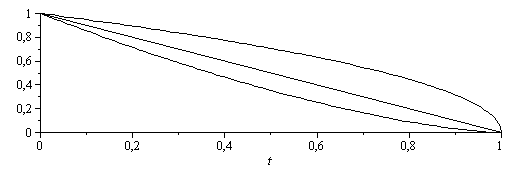c) Establecer el balance energético a través de una superficie de radio intermedio entre la gota y la llama.

>

eqBE:=Acc=Prod+Diff_flux+Conv_flux;eqBE:=0=-mdotF*hlv0+A*k*Diff(T,r)-mdot*c[pF]*(T-T0);eqBE:=0=-hlv0+(k/(rho*v))*Diff(T,r)-c[pF]*(T-T0);eqBE:=dT/(hlv0+c[pF]*(T-T0))=-rho*v*dr/k;eqBE:=ln(1+c[pF]*(Tad-T0)/hlv0)=c[pF]*rho*v0*r0^2*(1/r0-1/r1)/k;eqI:=rho*v0=-rho[liq]*dr0/dt;eqBE:=dr0^2/dt=-(2*k/(rho[liq]*c[pF]))*ln(1+c[pF]*(Tad-T0)/hlv0);

d) Calcular el tiempo de quemado.

>	eqt:=t[q]=(D/2)^2/((2*k/(rho[liq]*c[pF]))*ln(1+c[pF]*(Tad-T0)/h[lv0]));evalf(subs(dat,rho[liq]=rho,c[pF]=c[p],Tad=Ta_,Fdat,dat,%)):evalf(%,2);

i.e. las gotas tardan unos 25 ms en arder, habiendo tomado las propiedades constantes (pese a que la k_aire, e.g. varía de 0.025 W/(m·K) a 300 K a 0.090 W/(m·K) a 1400 K, que sería la temperatura media apropiada.

Para comparación con la realidad, una gota de 0,194 mm se consumiría en 0,092 s con este modelo, mientras que el resultado experimental es de 0,064 s (y eso que durante los primeros 10 ms no arde tan deprisa como la ley del cuadrado).

>