>	restart:#"m16_p22"

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):

Se dispone un tubo troncocónico horizontal de 20 cm de longitud, de cuarzo, de 1 cm de diámetro pequeño y 2,5 cm de diámetro mayor, abierto al aire por el lado ancho. Por el otro extremo se introduce 10-5 m3/s de propano, que se enciende en el lado ancho. Se pide:
a) Hacer un esquema de la instalación y del tipo de llama esperada, determinando la velocidad media de salida.
b) Determinar la cantidad de aire que habra que introducir por el lado estrecho para conseguir mezcla estequiométrica (manteniendo el gasto de combustible), calculando la velocidad de salida de la mezcla y haciendo un esquema de la llama esperada.
c)  Indicar qué ocurriría al ir aumentando gradualmente el gaso de aire mencionado desde cero al estequiométrico, y luego al ir disminuyéndolo.

d) Potencia térmica y temperatura máxima de llama.

Datos:

>	su1:="Aire":su2:="H2O":fuel:=C3H8;fuel_:=convert(fuel,string):dat:=[L=0.2*m_,D1=0.01*m_,D2=0.025*m_,Qf=1e-5*m_^3/s_];

Esquema:

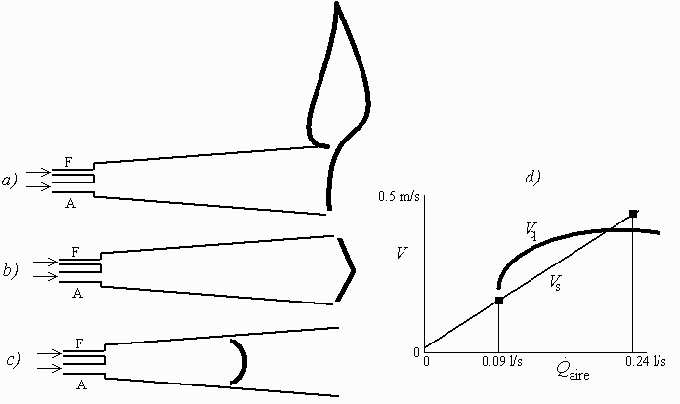
Eqs. const.:

>	Adat:=get_gas_data(su1):gdat:=get_gas_data(fuel_):ldat:=get_liq_data(fuel_):dat:=op(dat),op(subs(g=g0,[Const])),gdat,ldat,SI2,SI1:

a) Hacer un esquema de la instalación y del tipo de llama esperado, determinando la velocidad media de salida.

>	Vs:=Qs/As;As_:=evalf(subs(dat,Pi*D2^2/4));Vs_:=evalf(subs(Qs=Qf,As=As_,dat,Vs));

i.e, suponiendo que el perfil de velocidades a la salida fuera plano, la velocidad sería de 2 cm/s, y al encenderse (e.g. con chispa o llama piloto) daría lugar a una llama de difusión, amarillenta y con penacho vertical por causa de la flotabilidad y las bajas velocidades (ver Fig. 1a). Una idea del orden de magnitud de la altura de llama nos la daría el modelo difusivo axilsimétrico, pese a la gran diferencia de geometría.

>	'Re'=Vs*Ds/nu;nu=mu/rho;nu:=mu*R*T0/p0;nu_:=evalf(subs(Adat,dat,nu)):'nu[air]'=evalf(%);Re_:=evalf(subs(dat,Vs_*D2/nu_));Lfl:='Vs*Ds^2/(4*Di)';'Di=nu';Di:=nu_:Lfl_:=subs(Qs=Qf,As=As_,Ds=D2,dat,Lfl);

b) Determinar la cantidad de aire que habría que introducir por el lado estrecho para conseguir mezcla estequiométrica (manteniendo el gasto de combustible), calculando la velocidad de salida de la mezcla y haciendo un esquema de la llama esperada.

>	A0_:=rhs(Ateo(fuel));Qa:=A0*Qf;Qa_:=subs(dat,A0=A0_,Qa);Vs_:=evalf(subs(Qs=Qa_,As=As_,dat,Vs));

i.e, suponiendo que el perfil de velocidades a la salida fuera plano, la velocidad sería de 0,49 m/s, y al encenderse se formaría una llama de premezcla ligeramente cnica (Fig. 1b), puesto que la velocidad de deflagración estequiométrica es de 0,45 m/s (Tabla A3.9), si bien las llamas de premezcla tan planas son muy inestables (ver apartado siguiente).

c)  Indicar qué ocurriría al ir aumentando gradualmente el gaso de aire mencionado desde cero al estequiométrico, y luego al ir disminuyéndolo.

De la Tabla A3.9, para el propano, LIP=2%, LIR=10%; el LIP puede comprobarse por la aproximación de la mitad de la estequiometría.

>

LIP:=(1/2)/(1+A0);LIP_:=evalf(subs(A0=A0_,LIP));eqLIP:=Qf/(Qf+QaLIP)=(1/2)*Qf/(Qf+QaSTQ);QaLIP_:=solve(%,QaLIP);QaLIP__:=subs(QaSTQ=Qa_,dat,QaLIP_);Vs_:=evalf(subs(Qs=QaLIP__,As=As_,dat,Vs));eqLIR:=Qf/(Qf+QaLIR)=10/100;QaLIR_:=solve(%,QaLIR);QaLIR__:=subs(QaSTQ=Qa_,dat,QaLIR_);Vs_:=evalf(subs(Qs=QaLIR__,As=As_,dat,Vs));

Al ir incrementando el caudal de aire, y en función de la velocidad media de salida en lugar del caudal de aire (que son proporcionales), se observaría lo siguiente: desde 0 a 0,18 m/s (límite de ignición rico) no habra más que una llama de difusión cada vez más larga por el barrido del aire; a los 0,18 m/s o algo más podría formarse (dependerá de los detalles de la velocidad de deflagración de mezclas ricas; según el esquema hipotético de la Fig. 1.d no se formaría) una llama de premezcla rica (verdosa) a la salida, encendida por la llama de difusión en la que se seguiría quemando el resto de combustible.

Al seguir aumentando el aire desde 0,18 m/s a los 0,49 m/s de la estequiometría, si se ha formado la llama de premezcla, ésta se haría más intensa y la de difusión iría desvaneciéndose hasta desaparecer; si no se ha formado, se formará en el punto de intersección de la Fig. 1d, i.e. cuando la velocidad de salida sea prácticamente 0,45 m/s.

Si se siguiera incrementando el aire más allá de la estequiometra sólo quedaría la llama de premezcla que se haría más violeta hasta apagarse por desprendimiento del borde o por límite de ignición pobre (LIP).

Al disminuir el caudal de aire por debajo del estequiométrico la llama de premezcla se hará más plana, aparecerá otra vez la de difusión, pero la primera se moverá corriente arriba hasta estabilizarse en una posición como la de la Fig. 1c (incluso puede que, como ya era muy plana, no se estabilice la configuración) Fig. 1b).

d) Potencia térmica y temperatura máxima de llama.

>

eq:=eq_fit(fuel+a*O2=b*CO2+d*H2O);Q:=PCS*nf;PCS_:=PCS(eq);nf:=p0*Qf/(R[u]*T0);nf_:=subs(dat,nf);'Q'=evalf(subs(dat,PCS_*nf_));eqMIX(a*fuel+a*A0*(c21*O2+c79*N2)=[2,3,4,6]);A0:=rhs(Ateo(fuel));sol1_:=subs(dat,solve({eqNX,eqBC,eqBH,eqBO,eqBN},{a,x[O2],x[N2],x[CO2],x[H2O]}));i:='i':PCI_:=PCI(eq):Ta_:=subs(cpComp_,sol1_,dat,rhs(eq15_7_3));

La potencia térmica es de 920 W en todo momento, entre aire o no, mientras que la temperatura de la llama será máxima, 2400 K, sólo para la llama de premezcla estequiométrica, siendo algo menor para las llamas de difusión y para las premezclas no estequiométricas.

>