>	restart:#"m16_p20"

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):

Por la boca de un tubo vertical de 4 mm de diámetro sale hacia arriba un flujo de gas natural a 0,1 m/s. Coaxialmente se insufla aire puro a la misma velocidad por un conducto anular de 16 mm de diámetro exterior (los espesores de los tubos son muy pequeños. Se pide:
a) Hacer un esquema y razonar en qué regiones sería inflamable la mezcla, el tipo de llama que se desarrollaría, su movimiento, geometría, color, etc.
b)  Plantear el problema de difusión (sin reacción) que determinaría la distribución radial y estacionaria de propano a z=1 cm de altura de la boca del tubo interior, relacionando el coeficiente de difusión con la conductividad térmica según la teoría cinética de gases.
c)  Suponiendo que para esa distancia los efectos axilsimétricos y de contorno todavía no son importantes, ensayar una solución de semejanza, del tipo:

d) Plantear la resolución numérica del problema difusivo axilsimétrico mediante diferencias finitas, eligiendo adecuadamente la discretización.

Datos:

>	su1:="Aire":su2:="H2O":su3:="CH4":dat:=[Mf_=0.016*kg_/mol_,R1=2e-3*m_,y[F0]=1,V=0.1*m_/s_,R2=8e-3*m_,z1=0.01*m_];

Eqs. const.:

>	Adat:=get_gas_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):Fdat:=get_gas_data(su3),get_liq_data(su3):dat:=op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:

a) Hacer un esquema y razonar en qué regiones sería inflamable la mezcla, el tipo de llama que se desarrollaría, su movimiento, geometría, color, etc.

Las mezclas metano/aire sólo son inflamables si xF está entre el 5% y el 15%.

Como antes de la mezcla xF=100% y después xF=(R1/R2)^2=(2/8)^2=6%:

Sí se podría encender una llama de premezcla verdosa corriente abajo, pero no se estabilizaría sino que viajaría a unos (0,1-0,4)=-0,3 m/s, es decir, corriente arriba hasta apagarse en la unión (habiendo tomado Vq=0,4 m/s).

Sí se podría encender una llama de difusión amarillenta anclada al borde, y que al ser sobreventilada (xFesteq=10%) se cierra hacia el eje, con una altura estimada de V*R1^2/Di=0,1*2^2*1e-6/0.8e-5=0,05 m.

b)  Plantear el problema de difusión (sin reacción) que determinaría la distribución radial y estacionaria de propano a z=1 cm de altura de la boca del tubo interior, relacionando el coeficiente de difusión con la conductividad térmica según la teoría cinética de gases

>	eqDIF:=v*diff(y[F](r,z),z)=simplify(Di*(1/r)*diff(r*diff(y[F](r,z),r),r));y[F](r,0):=piecewise(r<R[1],y[F0]);diff(y[F](r,z),r)=0;diff(y[F](r,z),r)=0;Di:=k/(rho*c[p]);rhoF_:=subs(p=p0,T=T0,dat,rhs(eq1_12));Di_:=subs(rho=rhoF_,Fdat,dat,Di);

c)  Suponiendo que para esa distancia los efectos axilsimétricos y de contorno todavía no son importantes, ensayar una solución de semejanza, del tipo:

>	diff(y[F](r,z),z)=diff(y[F](eta),eta)*diff(r/sqrt(z),z);diff(y[F](r,z),r)=diff(y[F](eta),eta)*diff(r/sqrt(z),r);diff(y[F](r,z),r,r)=diff(y[F](eta),eta,eta)*diff(r/sqrt(z),r)*diff(r/sqrt(z),r);

>	z*(simplify(subs(r=eta*sqrt(z),(V*diff(y[F](eta),eta)*diff(r/sqrt(z),z)=0*(Di/r)*diff(y[F](eta),eta)*diff(r/sqrt(z),r)+Di*diff(y[F](eta),eta,eta)*diff(r/sqrt(z),r)*diff(r/sqrt(z),r)))));

>	dsolve({y[F](-10)=y[F0],y[F](10)=0,diff(y[F](eta),eta,eta)+(V/(2*Di))*diff(y[F](eta),eta)*eta=0},y[F](eta));assign(%):

>

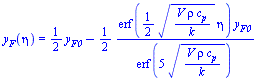>	eqY:=y[F1]=subs(eta=r/sqrt(z),z=z1,rho=rhoF_,Fdat,y[F](eta));eqY_:=y[F1]=series(rhs(eqY),r=0,2);

>	plot(subs(dat,SI0,{[[-R1/m_,0],[-R1/m_,1]],[[R2/m_,0],[R2/m_,1]],rhs(eqY)}),r=-.002..0.008,color=black);

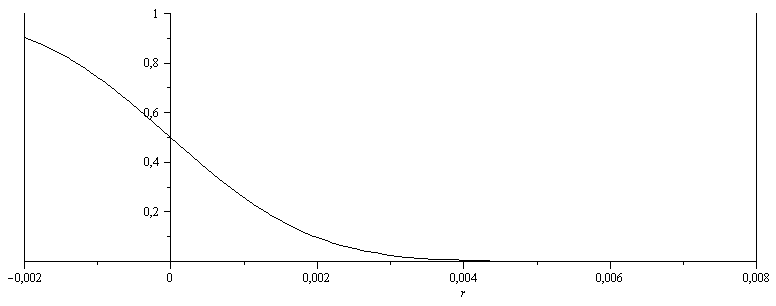d) Plantear la resolución numérica del problema difusivo axilsimétrico mediante diferencias finitas, eligiendo adecuadamente la discretización.

>	eqDIS:=v*(y[F](r,z+dz)-y[F](r,z))/dz=D[i]*(y[F](r+dr,z)-2*y[F](r,z)+y[F](r-dr,z))/(dr)^2+(D[i]/r)*(y[F](r+dr,z)-y[F](r-dr,z))/(2*dr);eqCON1:=y[F](0,z+dz)=y[F](dr,z+dz);eqCON2:=y[F](R2,z+dz)=y[F](R2-dr,z+dz);

La discretización más gruesa sería con dr=R1/2=1 mm, y para que fuese estable habría de ser dz<(1/2)*(v/Di)*dr^2=(1/2)*(0,1/0.8e-5)*1e-6=0,006 m.

Para ver lo que pasa a 1 cm convendría elegir dr=0,5 mm y dz=(1/2)*(v/Di)*dr^2= (1/2)*(0,1/5e-6)/1e6=1 cm o algo así.

>