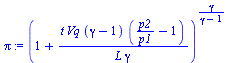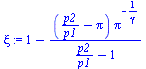>	restart:#"m16_p15"

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):

Se quema propano con un 50% de exceso de aire en la boca de un mechero cilíndrico horizontal de 25 mm de diámetro, observándose que la longitud de la llama es igual al diámetro del tubo. Se ha medido la velocidad media de los gases en el tubo, que tiene 10 m de longitud, y resulta ser de 1,3 m/s.. Se pide:
a) Calcular el aire teórico (en base molar y en base másica) y los gastos másicos de propano y de aire realmente usados.
b) Calcular la composición esperada de los gases de escape.
c) Calcular el poder calorífico y la temperatura de combustión adiabática, indicando la influencia de la relación aire/combustible.
d) Calcular la velocidad de deflagración laminar.
e) Si se produjese una ignición corriente arriba del tubo, calcular la velocidad relativa de la llama.
f) Supóngase que se llena el tubo de mezcla combustible en reposo y en un instante dado se produce la ignición en un extremo del tubo. Indicar cómo se calcularía la velocidad de la llama respecto al tubo en los cuatro casos posibles de condiciones de confinamiento: tubo cerrado por ambos extremos, abierto por uno de ellos o abierto por ambos extremos.
g) Calcular la velocidad aparente de la llama en el caso de ambos extremos cerrados
Datos:

>	su1:="Aire":su2:="H2O":su3:="C3H8":dat:=[c[v]=25*J_/(mol_*K_),u=3,v=8,w=0,o=0,y=0,e=0.5,D=0.025*m_,H=D,L=10*m_,V=1.3*m_/s_];

Eqs. const.:

>	Adat:=get_gas_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):Fdat:=get_gas_data(su3):dat:=Mf_=subs(Fdat,M),op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:

a) Calcular el aire teórico (en base molar y en base másica) y los gastos másicos de propano y de aire realmente usados.

>

eq1:=eq15_2;eq2:=eq15_4;eq1_:=subs(dat,eq1);A0m_:=subs(eq1_,dat,A[0]*M/Mf_);A_:=solve(subs(eq1_,dat,eq2),A);Am_:=subs(eq1_,dat,A_*M/Mf_);eqBM:=ndot=p0*Vdot/(R[u]*T0);eqBM_:=evalf(subs(Const,Vdot=V*Pi*D^2/4,dat,eqBM));mf:=ndot*Mf*1/(1+A);mf_:=subs(eqBM_,Mf=Mf_,A=A_,mf);ma:=ndot*M*A/(1+A);ma_:=subs(eqBM_,Adat,A=A_,ma);

b) Calcular la composición esperada de los gases de escape.

>	eq:=eqMIX(a*C3H8+b*(c21*O2+c79*N2)=[2,3,4,5]);eqDat:=b/a=A_;sol1_:=solve(subs(dat,{eqNX,eqBC,eqBH,eqBO,eqBN,eqDat}),{a,b,x[Comp[2]],x[Comp[3]],x[Comp[4]],x[Comp[5]]});

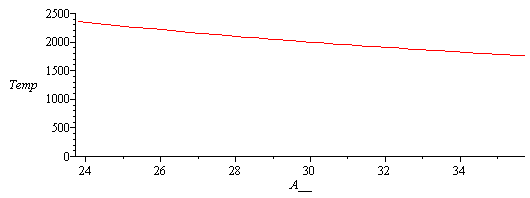
c) Calcular el poder calorífico y la temperatura de combustión adiabática, indicando la influencia de la relación aire/combustible.

>

PCI_:=PCI(subs(sol1_,eq/a));eq15_7_2;Ta_:=subs(cpComp_,sol1_,dat,T25+a*PCI_/sum(delta[i]*x[Comp[i]]*c[p,Comp[i]],i=1..C_));eqDat:=b/a=A__;sol1__:=solve(subs(dat,{eqNX,eqBC,eqBH,eqBO,eqBN,eqDat}),{a,b,x[Comp[2]],x[Comp[3]],x[Comp[4]],x[Comp[5]]}):Ta__:=subs(cpComp_,sol1__,dat,T25+a*PCI_/sum(delta[i]*x[Comp[i]]*c[p,Comp[i]],i=1..C_)):plot(subs(SI0,Ta__),A__=subs(eq1_,A[0])..A_,Temp=0..2500);

d) Calcular la velocidad de deflagración laminar.

Del triángulo de velocidades en la boca del tubo se deduce:

>	eqGEO:=arcsin(Vq/V)=arctan((D/2)/H);Vq_:=solve(subs(dat,dat,eqGEO),Vq);

e) Si se produjese una ignición corriente arriba del tubo, calcular la velocidad relativa de la llama.

La llama, inicialmente esférica, al llegar a las paredes se aproximaría a dos llamas planas (despreciando la flotabilidad) a velocidades:

>	V1:=V+Vq;V2:=V-Vq;V1_:=subs(dat,V+Vq_);V2_:=subs(dat,V-Vq_);

Al llegar la de V1 a la boca apagaría la que allí estaba anclada. Al llegar la de V2 no tendría tiempo de estabilizarse y se apagaría por difusión en la atm.

f) Supóngase que se llena el tubo de mezcla combustible en reposo y en un instante dado se produce la ignición en un extremo del tubo. Indicar cómo se calcularía la velocidad de la llama respecto al tubo en los cuatro casos posibles de condiciones de confinamiento: tubo cerrado por ambos extremos, abierto por uno de ellos o abierto por ambos extremos.

Llamando S al área, x a la posición de la llama y xp a su velocidad.

Abierto-Cerrado

>

nf1_:=evalf(subs(Const,dat,(1/(1+A_))*(p0*L*Pi*D^2/4)/(R[u]*T0)));eqETi:=p1*S*L=(1+A)*nf1*R[u]*T1;eqETtF:=p1*S*(L-x)=(1+A)*nf*R[u]*T1;eqETtB:=p1*S*(x+x[B])=(1+A)*(nf1-nf)*R[u]*TB;eqKIN:=xp=Vq;eqBF:=Dp=rho[B]*xBp^2;eq1:=lhs(eqETtF)/lhs(eqETi)=rhs(eqETtF)/rhs(eqETi);eq1dif:=-xp/L=nfp/nf1;eq2:=lhs(eqETtB)/lhs(eqETi)=rhs(eqETtB)/rhs(eqETi);eq2dif:=xp/L+xBp/L=-(nfp/nf1)*(TB/T1);sol1:=solve({eq1dif,eq2dif,eqKIN,eqBF},{xp,xBp,nfp,Dp});sol1_:=subs(Vq=Vq_,nf1=nf1_,T1=T0,p1=p0,TB=Ta_,rho[B]=subs(p=p0,T=Ta_,rhs(eq1_12)),dat,sol1);

Cerrado-Abierto

>

eqETi:=p1*S*L=(1+A)*nf1*R[u]*T1;eqETtF:=p1*S*(x[F]-x)=(1+A)*nf*R[u]*T1;eqETtB:=p1*S*(x)=(1+A)*(nf1-nf)*R[u]*TB;eqKIN:=xp=Vq+xFp;eqBF:=Dp=rho[F]*xFp^2;eq1:=lhs(eqETtF)/lhs(eqETi)=rhs(eqETtF)/rhs(eqETi);eq1dif:=xFp/L-xp/L=nfp/nf1;eq2:=lhs(eqETtB)/lhs(eqETi)=rhs(eqETtB)/rhs(eqETi);eq2dif:=xp/L=-(nfp/nf1)*(TB/T1);sol1:=solve({eq1dif,eq2dif,eqKIN,eqBF},{xp,xFp,nfp,Dp});sol1_:=subs(Vq=Vq_,nf1=nf1_,T1=T0,p1=p0,TB=Ta_,rho[F]=subs(p=p0,T=T0,rhs(eq1_12)),dat,sol1);

Abierto-Abierto

>

eqETi:=p1*S*L=(1+A)*nf1*R[u]*T1;eqETtF:=p1*S*(x[F]-x)=(1+A)*nf*R[u]*T1;eqETtB:=p1*S*(x+x[B])=(1+A)*(nf1-nf)*R[u]*TB;eqKIN:=xp=Vq+xFp;eqBF:=rho[F]*xFp^2=rho[B]*xBp^2;eq1:=lhs(eqETtF)/lhs(eqETi)=rhs(eqETtF)/rhs(eqETi);eq1dif:=xFp/L-xp/L=nfp/nf1;eq2:=lhs(eqETtB)/lhs(eqETi)=rhs(eqETtB)/rhs(eqETi);eq2dif:=xp/L+xBp/L=-(nfp/nf1)*(TB/T1);sol1:=solve({eq1dif,eq2dif,eqKIN,eqBF},{xp,xFp,nfp,xBp});sol1_:=allvalues(subs(Vq=Vq_,nf1=nf1_,T1=T0,p1=p0,TB=Ta_,rho[F]=subs(p=p0,T=T0,rhs(eq1_12)),rho[B]=subs(p=p0,T=Ta_,rhs(eq1_12)),dat,SI0,sol1))[2];

Cerrado-Cerrado

>

eqETi:=p1*S*L=(1+A)*nf1*R[u]*T1;eqETtF:=p*S*(L-x)=(1+A)*nf*R[u]*T1;eqETtB:=p*S*(x)=(2+A)*(nf1-nf)*R[u]*TB;eqETf:=p2*S*L=(2+A)*nf1*R[u]*TB2;eqKIN:=xp=Vq+((L-x)/(gamma*p))*pp;eqBF:=Dp=rho[F]*xFp^2;eqBEF:=TF/T1=(p/p1)^((gamma-1)/gamma);eqBEt:=(nf1-nf)*PCI=(2+A)*(nf1-nf)*c[v]*(TB-T1)+(1+A)*nf*c[v]*(TF-T1);eqBEf:=nf1*PCI=(2+A)*nf1*c[v]*(TB2-T1);#eq1:=lhs(eqETtF)/lhs(eqETi)=rhs(eqETtF)/rhs(eqETi);eq2:=lhs(eqETtB)/lhs(eqETi)=rhs(eqETtB)/rhs(eqETi);#sol1:=solve({eq1dif,eq2dif,eqKIN,eqBF},{xp,xFp,nfp,Dp});sol1_:=subs(Vq=Vq_,nf1=nf1_,T1=T0,p1=p0,TB=Ta_,rho[F]=subs(p=p0,T=T0,rhs(eq1_12)),dat,sol1);

>

>	TB2_:=subs(PCI=PCI_,A=A_,T1=T0,dat,solve(eqBEf,TB2));p2_:=subs(dat,evalf(subs(Const,nf1=nf1_,TB2=TB2_,PCI=PCI_,A=A_,S=Pi*D^2/4,T1=T0,dat,solve(eqETf,p2))));

>

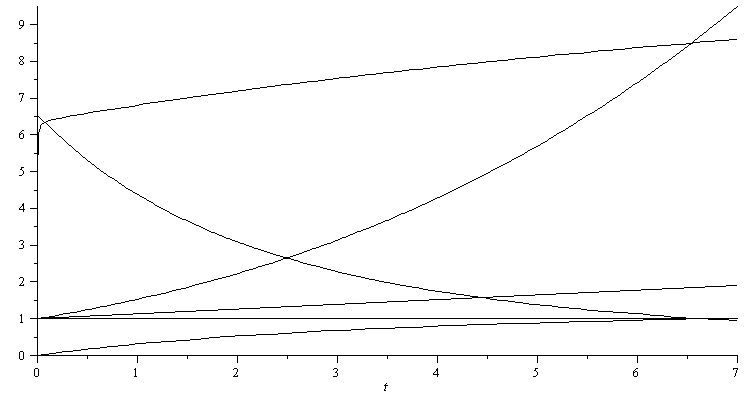
tau:=t*Vq/L;pi:=(1+tau*((gamma-1)/gamma)*(p2/p1-1))^(gamma/(gamma-1));thetaF:=1+tau*((gamma-1)/gamma)*(((2+A)/(1+A))*(TB2/T1)-1);xip:='1+(p2/p1)/((gamma*pi))-1/gamma';xi:='1-((p2/p1-pi)/(p2/p1-1))*pi^(-1/gamma)';thetaB:='pi*xi*((1+A)/(2+A))*((p2/p1-1)/(pi-1))';plot(subs(Vq=Vq_,A=A_,TB2=TB2_,T1=T0,p1=p0,p2=p2_,dat,SI0,{pi,thetaF,thetaB,xip,xi,1}),t=0..7,color=black);

>