>	restart:#"m16_p13"

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):

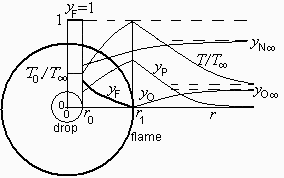
Considérese la combustión cuasi estacionaria y esférica de una gota de benceno 3 mm de diámetro en aire. Se pide:
a) Poder calorífico y temperatura adiabática.
b) Constante de quemado,   (r2 r2inicial)/t (compárese con el valor experimental (d2 d2inicial)/t = 0,96 mm2/s.
c) Posición relativa de la llama.

d) Fracción másica de vapor de combustible cerca de la gota.

Datos:

>	su1:="Aire":su2:="C6H6":dat:=[D=3e-3*m_,beta=0.96e-6*m_^2/s_];

>	Adat:=get_gas_data(su1):Fdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):dat:=op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:

a) Poder calorífico y temperatura adiabática

>

eq:=eq_fit(C6H6+c1*O2=c2*CO2+c3*H2O);eq1:=eq15_2;eqA:=Ateo(su2);eq:=C6H6+(15/2)*O2=6*CO2+3*H2O:PCI_:=PCI(eq);PCIm_:=subs(dat,PCI_/rhs(Mf(su2)));PCS_:=PCS(eq);PCSm_:=subs(dat,PCS_/rhs(Mf(su2)));eq:=eqMIX(a*C6H6+b*(c21*O2+c79*N2)=[3,4,5]);sol1_:=solve(subs(b=rhs(eqA)*a,c=0,d=0,dat,dat,{eqNX,eqBC,eqBH,eqBO,eqBN}),{a,x[Comp[3]],x[Comp[4]],x[Comp[5]]});eq15_7_2;Ta_:=subs(sol1_,cpComp_,dat,T25+a*PCI_/sum(delta[i]*x[Comp[i]]*c[p,Comp[i]],i=1..C_));

i.e. PCI=3.1 MJ/mol=40 MJ/kg y Ta=2500 K.

b) Constante de quemado, b _ (r2 r2inicial)/t (compárese con el valor experimental (d2 d2inicial)/t = 0,96 mm2/s.

Suponemos conocida la expresión de la constante de la ley de quemado (ley del cuadrado del radio).

Se obtinen directamente del balance energético de una esfera de radio r>r0 (y r<rF).

>

eqR:=r(t)^2=r[0]^2-beta*t;eqB:=beta=(2*k/(rho[liq]*c[p]))*ln(1+c[p]*(Ta-To)/h[lv0]);eqrholiq:=rho[liq]=subs(Fdat,rho);k0:=subs(Adat,k);kT:='k0'*T/T0;kT_:=evalf(subs(T=Ta_,dat,kT));cp0:=subs(Adat,c[p]);hlv0:=subs(Fdat,h[lv0]);To=T[v,p0];Tvp0_:=evalf(subs(dat,solve(p0=pv(T),T)));'T[b]'=subs(Fdat,T[b]);eqB_:=evalf(subs(Ta=Ta_,To=Tvp0_,k=kT_,eqrholiq,Adat,Fdat,SI2,eqB));eqerr:=beta/beta[data]=subs(dat,rhs(eqB_/beta));plot(subs(eqB_,dat,SI0,sqrt((D/2)^2-beta*t)),t=0..3,r=0..0.002);

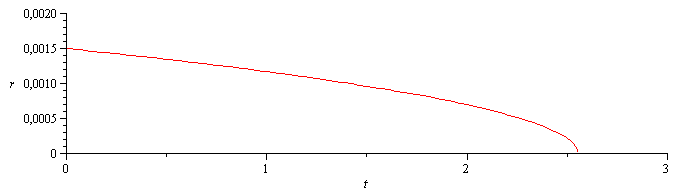i.e. el ajuste es casi perfecto (un 92% del experimental).

c) Posición relativa de la llama.

Se obtiene del balance másico de oxidante en una esfera de radio r>rF.

>

eqBM_O:=0=mdotO+A*D[O]*rho*dy[O]/dr-rho*v*A*y[O];eqBM_O:=0=-nu[O]*M[O]/M[F]+(D[O]/v)*dy[O]/dr-y[O];eqBM_O:=dy[O]/(nu[O]*M[O]/M[F]+y[O])=(v[0]*r[0]^2/(D[O]*r^2))*dr;eqBM_O:=ln((nu[O]*M[O]/M[F]+y[F,infinity])/(nu[O]*M[O]/M[F]))=-(v[0]*r[0]^2/D[O])*(0-1/r[F]);eqBM_I:=v[0]*rho=-rho[liq]*dr[0]/dt;eqBM_I:=v[0]*rho=rho[liq]*beta/(2*r[0]);eqBM_I_:=subs(eqB,%);eqair:=y[O,infinity]=c21*M[O]/M[m];eqnu:=nu[O]=15/2;eqrF:=r[F]=subs(eqB,k=rho*c[p]*D[O],(rho[liq]/rho)*(beta/2)*r[0]/(D[O]*ln((nu[O]*M[O]/M[F]+y[O,infinity])/(nu[O]*M[O]/M[F]))));eqrF_:=evalf(subs(eqair,M[O]=0.032*kg_/mol_,M[F]=rhs(Mf(fuel)),eqnu,Ta=Ta_,To=Tvp0_,h[lv0]=hlv0,M[m]=M,dat,%));

i.e. la llama se estabiliza a unos 26 radios de la gota (entre 20 y 30, atendiendo a la incertidumbre).

d) Fracción másica de vapor de combustible cerca de la gota.

Se obtiene del balance másico de combustible en una esfera de radio r>r0 (y r<rF).

>

eqBM_F:=0=mdotF+A*D[F]*rho*dy[F]/dr-rho*v*A*y[F];eqBM_F:=0=1+(D[F]/v)*dy[F]/dr-y[F];eqBM_F:=dy[F]/(1-y[F])=-(v[0]*r[0]^2/(D[F]*r^2))*dr;eqBM_F:=ln(1/(1-y[F,0]))=(v[0]*r[0]^2/D[F])*(1/r[0]-1/r[F]);eqBM_F_:=subs(r[F]=infinity,eqBM_I_/rho,k=rho*c[p]*D[F],%);eqBM_F__:=1/(1-y[F,0])=1+c[p]*(Ta-To)/h[lv0];eqyF0:=y[F,0]=solve(%,y[F,0]);eqyF0_:=subs(Ta=Ta_,To=Tvp0_,h[lv0]=hlv0,dat,%):evalf(%,2);

i.e. el 85% en masa de los gases cercanos a la gota son vapor de combustible.

>