>	restart:#"m16_p11"

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):

Se pretende estudiar la evolución temporal en el proceso de combustión esférica descrito en el problema P 15.27 (R = 0,4 m, p1 = 100 kPa, T1 = 293 K, x1 = 0,033). Se pide:

a) Indicar qué relación habrá entre la velocidad de deflagración laminar, Vq, y la velocidad aparente de la llama al comienzo y al final de la combustión.

b) Relacionar Vq con la velocidad aparente de la llama y el perfil temporal de presiones

.c) Relacionar la presión con la posición del frente de llama.

d) Variación de la presión con el tiempo cuando t Æ 0.

e) Despreciando el efecto de la temperatura en Vq y suponiendo Vq = 0,5 m/s representar la evolución en función del tiempo y en función de la presión.

Datos:

>	su1:="Aire":su2:="H2O":su3:="C4H10":dat:=[Mf_=0.058*kg_/mol_,R_=0.4*m_,T0=(20+273)*K_,xf=0.033,Vq=0.5*m_/s_];

Esquema:

Eqs. const.:

>	Adat:=get_gas_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):dat:=op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:Fdat:=get_gas_data(su3),get_liq_data(su3):

a) Razonar por qué se mide la variación de la presión con el tiempo y no otras variables.) Indicar qué relación habrá entre la velocidad de deflagración laminar, Vq, y la velocidad aparente de la llama al comienzo y al final de la combustión.

Porque la p es uniforme y la T no.

b) Calcular la masa, densidad y cantidad de sustancia iniciales.

>	eq1:=subs(eq1_11,R=R[u]/Mm,eq1_12);Mm_:=subs(dat,xf*Mf_+(1-xf)*M);V_:=evalf(subs(dat,(4/3)*Pi*R_^3));eq1_:=m=evalf(subs(Const,V=V_,p=p0,Mm=Mm_,T=T0,dat,solve(eq1,m)));rho_:=subs(eq1_,m)/V_;n=m/Mm;n_:=subs(eq1_,m)/Mm_;

c) Calcular el aire teórico y la riqueza de la mezcla, y establecer el balance de especies y de cantidad de sustancia.

>	eq15_2;eq2_:=Ateo(su3);A_:=(1-xf)/xf;A_:=subs(dat,A_);eq15_3;phi=rhs(eq2_)/A_;eq:=eqMIX(a*C4H10+b*(c21*O2+c79*N2)=[3,4,5,7]);eqDat_:=b/a=A_;sol1_:=solve(subs(dat,{eqNX,eqBC,eqBH,eqBO,eqBN,eqDat_}),{a,b,x[N2],x[CO],x[CO2],x[H2O]});nf_ni:=1/(a+b);nf_ni_:=1/subs(sol1_,a+b);

d) Poder calorífico y temperatura de combustión adiabática, a p=cte y a V=cte. ¿Cuál sería la presión final cuando se atemperase el recipiente?.

Si fuera combustión completa:

>	eq0:=C4H10+(13/2)*O2=4*CO2+5*H2O;PCI_:=PCI(subs(sol1_,eq0));

Pero al formarse CO:

>	PCI_:=PCI(subs(sol1_,eq/a));

La corrección de PCIp=-Sum(nu.i*h.i) a PCIv=-Sum(nu.i*u.i)=-Sum(nu.i*h.i)+Sum(nu.i*p0*v.i)=-Sum(nu.i*h.i)+Sum(nu.i*Ru*T25/p0) es despreciable:

>	Dn_a:=subs(sol1_,(sum('delta[i]*x[Comp[i]]',i=1..C_)-a-b)/a);DPCI_:=subs(Const,dat,Dn_a*R[u]*T25);PCI_:=PCI_+DPCI_;

>	Ta_p:=subs(cpComp_,sol1_,dat,T25+a*PCI_/(sum(delta[i]*x[Comp[i]]*c[p,Comp[i]],i=1..C_)));subs(p=V,eq15_7_2);Ta_:=subs(cpComp_,sol1_,Const,dat,T25+a*PCI_/(sum(delta[i]*x[Comp[i]]*(c[p,Comp[i]]-R[u]),i=1..C_)));

>	eq8_4;xcond:=x[H2O]-xv;pv_:=subs(dat,evalf(subs(dat,pv(T0))));xv_:=subs(dat,phi=1,pv_/p0);xcond_:=subs(sol1_,x[H2O]-xv_);pf:='p0*(Sum('delta[i]*x[Comp[i]]',i=1..C)-xcond)/b';pf_:=subs(sol1_,dat,p0*(sum('delta[i]*x[Comp[i]]',i=1..C_)-xcond_)/b);

e) Presión al final de la combustión, y temperatura máxima en la región de gases frescos.

>	pf:=p0*(Ta/T0)*(Sum('delta[i]*x[Comp[i]]',i=1..C)/b);pf_:=subs(sol1_,dat,p0*(Ta_/T0)*(sum('delta[i]*x[Comp[i]]',i=1..C_)/b));Tmax:=T0*(pmax/p0)^((gamma-1)/gamma);Tmax_:=subs(pmax=pf_,dat,Tmax);

f) Demostrar que si se supone cv=cte, durante la evolución se verifica (p p1)/(p2 p1)=f, siendo f la fracción de butano quemada.

Sea 1+A los moles de entrada por mol de fuel.

Sea P=Sum(x.i)/a los moles de salida por mol de fuel.

f=nf/nf1 la fracción de fuel quemada.

>	F_:=subs(sol1_,1+b/a);P_:=subs(sol1_,sum('delta[i]*x[Comp[i]]',i=1..C_)/a);eqf:=f=nf/nf1;

>	eqETIni:=p1*V=(1+A)*nf1*R[u]*T1;nf1_:=subs(Const,p1=p0,V=V_,A=b/a,sol1_,T1=T0,dat,solve(eqETIni,nf1));

>	eqETInst:=p*V=P*nf*R[u]*T[B]+(1+A)*(nf1-nf)*R[u]*T[F];eqBEInst:=nf*PCI=P*nf*c[v]*(T[B]-T1)+(1+A)*(nf1-nf)*c[v]*(T[F]-T1);

>	eqETFin:=p2*V=P*nf1*R[u]*T[B2];eqBEFin:=nf1*PCI=P*nf1*c[v]*(T[B2]-T1);

>	sol1:=solve({eqETIni,eqETFin,eqBEFin},{nf1,T[B2],PCI});

>	sol2:=simplify(subs(sol1,solve({eqETInst,eqBEInst,eqf},{f,nf,T[B]})));

a) Indicar qué relación habrá entre la velocidad de deflagración laminar, Vq, y la velocidad aparente de la llama al comienzo y al final de la combustión.

Inicialmente es a p=cte y drB/dt=Vq*Ta/T0 y al final los frescos no se mueven y drB/dt=Vq (algo mayor porque T0 pasa a TF2)

>	eq1:=dr[B]/dt=Vq*Ta/T0;eq1:=dr[B]/dt=subs(dat,Vq*Ta_/T0);

b) Relacionar Vq con la velocidad aparente de la llama y el perfil temporal de presiones

>	eqKIN:=4*Pi*r[B]^2*Vq=4*Pi*r[B]^2*dr[B]/dt+dV[F]/dt;eqKIN:=4*Pi*r[B]^2*Vq=4*Pi*r[B]^2*dr[B]/dt-(V[F]/(gamma*p))*dp/dt;eqKIN:=4*Pi*r[B]^2*Vq=4*Pi*r[B]^2*dr[B]/dt-(4*Pi*(R^3-r[B]^3)/(3*gamma*p))*dp/dt;

.c) Relacionar la presión con la posición del frente de llama.

>	eqETIni;eqETInst_:=p*V[F]=(1+A)*(nf1-nf)*R[u]*T[F];eq1:=lhs(eqETInst_)/lhs(eqETIni)=rhs(eqETInst_)/rhs(eqETIni);eq1_:=simplify(subs(V[F]=R^3-r[B]^3,V=R^3,nf=nf1*f,sol2,T[F]=T1*(p/p1)^((gamma-1)/gamma),eq1));eq1__:=r[B]=solve(eq1_,r[B])[1];eq1___:=(r[B]/R)^3=1-(pi[2]-pi)/(pi[2]-1)*(1/pi^(1/gamma));

siendo pi=p/p1.

d) Variación de la presión con el tiempo cuando t Æ 0

Como al principio es drB/dt=Vq*Ta/T0, al principio la presión varía con t^3.

>	eq1lim:=subs(r[B]=Vq*(Ta/T1)*t,lhs(eq1___))=series(subs(pi[2]=a,rhs(eq1___)),pi=1,2);

e) Despreciando el efecto de la temperatura en Vq y suponiendo Vq = 0,5 m/s representar la evolución en función del tiempo y en función de la presión.

>

pi2:=subs(dat,pf_/p0);f_:=simplify(subs(dat,SI2,subs(sol2,p=pi*p1,p1=p0,p2=pf_,f)));rB_R:=subs(pi[2]=pi2,rhs(eq1___))^(1/3);TF_T1:=subs(dat,pi^((gamma-1)/gamma));TB_T1:=subs(T[F]=TF_T1*T0,T1=T0,dat,SI0,collect(simplify(subs(nf=nf1*f,sol2,Const,p=pi*p1,p1=p0,p2=pf_,P=P_,nf1=nf1_,V=V_,A=A_,solve(eqETInst,T[B])/T1)),T[F]));

>

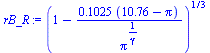deqKIN:=dt=subs(r[B]=R*rhs(eq1___)^(1/3),p=pi*p1,solve(eqKIN,dt));deqKIN:=Vq*t/R=int(expand(1+(1/(1-(pi[2]-pi)/(pi[2]-1)*(1/pi^(1/gamma)))-1)/(3*gamma*pi)),pi=1..pi_);dpi_dtVq_R:=expand(1/(1+(1/(1-(pi[2]-pi)/(pi[2]-1)*(1/pi^(1/gamma)))-1)/(3*gamma*pi)));dpi_dtVq_R_:=subs(pi[2]=pf_/p0,dat,dpi_dtVq_R);

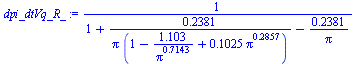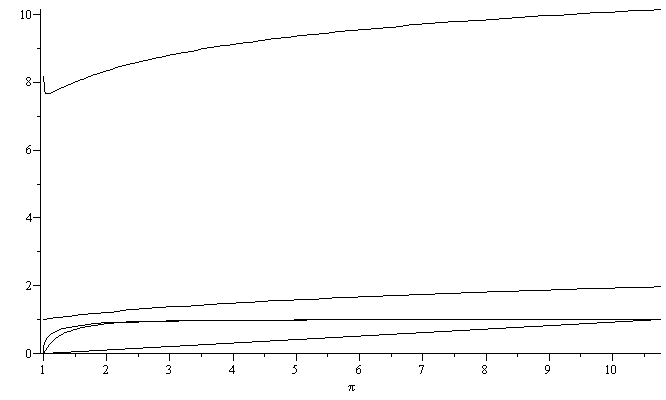
>	pl:=plot({f_,rB_R,TF_T1,TB_T1,dpi_dtVq_R_},pi=1..pi2,color=black):with(plots):display(pl);display(pl,view=[0..2,0..1]);

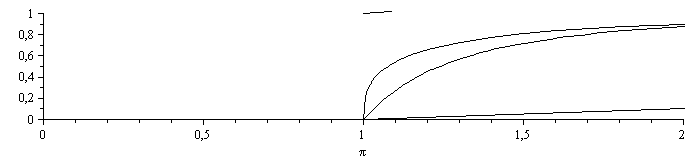Estas son las evoluciones en función de p/p1. No consigo hacerlo en función de t.

>