>	restart:#"m16_p07"

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):with(RealDomain):

En un reactor a presión constante se quema metano con oxígeno puro. Se pide:

a) Suponiendo combustión estequiométrica y completa, determinar la composición a la salida, el poder calorífico y la temperatura de salida

b) Sabiendo que en realidad se quema a razón de 2 moles de metano por cada 3 moles de oxígeno, y suponiendo que todo el hidrógeno se oxida completamente (y el carbono parcialmente), determinar la nueva estequiometría, la composición a la salida, el poder calorífico y la temperatura de salida

c) Sabiendo que en los productos aparecen CO2, CO, H2O y H2, y suponiendo que están en equilibrio, determinar el número de reacciones independientes necesarias para modelizar el proceso real, e indicarlas

d) Determinar las constantes de equilibrio de las reacciones anteriores en función de la temperatura, aproximándolas por lnK=A-B/T.

e) Plantear el sistema de ecuaciones que permiten determinar la composición, el poder calorífico y la temperatura de equilibrio adiabática en el proceso último, indicando las incógnitas y los datos.

Datos:

>	su1:="Aire":su2:="H2O":dat:=[Mf_=0.016*kg_/mol_,nf=2*mol_,nO=3*mol_,nCO2_1=0.1*mol_,nCO2_2=0.9*mol_];

Eqs. const.:

>	Adat:=get_gas_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):dat:=op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:

a) Suponiendo combustión estequiométrica y completa, determinar la composición a la salida, el poder calorífico y la temperatura de salida

>	eqM:=eqMIX(a*CH4+b*O2=[4,5]);sol1_:=evalf(solve(subs(dat,{eqNX,eqBC,eqBH,eqBO}),{a,b,x[Comp[4]],x[Comp[5]]}));PCI_:=PCI(subs(sol1_,eqM/a));eqBE_:=0=subs(cpComp_,sol1_,dat,PCI_-sum(delta[i]*x[Comp[i]]*c[p,Comp[i]],i=1..C_)*(Ts-T25)/a);Ts_:=subs(dat,solve(eqBE_,Ts));eqM_:=subs(sol1_,eqM/a);

Pero no será válido porque se descompone a tan alta temperatura.

b) Sabiendo que en realidad se quema a razón de 2 moles de metano por cada 3 moles de oxígeno, y suponiendo que todo el hidrógeno se oxida completamente (y el carbono parcialmente), determinar la nueva estequiometría, la composición a la salida, el poder calorífico y la temperatura de salida

>

eqDat:=b/a=subs(dat,nO/nf);eqM:=eqMIX(a*CH4+b*O2=[4,6,7]);sol1_:=evalf(solve(subs(dat,{eqNX,eqBC,eqBH,eqBO,eqDat}),{a,b,x[Comp[4]],x[Comp[6]],x[Comp[7]]}));PCI_:=PCI(subs(sol1_,eqM/a));eqBE_:=0=subs(cpComp_,sol1_,dat,PCI_-sum(delta[i]*x[Comp[i]]*c[p,Comp[i]],i=1..C_)*(Ts-T25)/a);Ts_:=subs(dat,solve(eqBE_,Ts));eqM_:=subs(sol1_,eqM/a);

Pero no es válido porque se descompone a tan altas T.

c) Sabiendo que en los productos aparecen CO2, CO, H2O y H2, y suponiendo que están en equilibrio, determinar el número de reacciones independientes necesarias para modelizar el proceso real, e indicarlas.

Si C={CH4,O2,CO2,CO,H2O,H2}, entonces R=C-E=6-3=3. Valen cualesquiera terna independiente, e.g. CO+H2O=CO2+H2, CO+(1/2)O2=CO2, y CH4+O2=CO2+2H2.

d) Determinar las constantes de equilibrio de las reacciones anteriores en función de la temperatura, aproximándolas por lnK=A-B/T.

>	eq9_20;eq9_25;eq1:=subs(p=p0,eqEQ(CO+H2O=CO2+H2));eq2:=subs(p=p0,eqEQ(CO+(1/2)*O2=CO2));;eq3:=subs(p=p0,eqEQ(CH4+O2=CO2+2*H2));ln(lhs(eq1))=evalf(expand(ln(rhs(eq1)))),ln(lhs(eq2))=evalf(expand(ln(rhs(eq2)))),ln(lhs(eq3))=evalf(expand(ln(rhs(eq3))));

>	eqM:=eqMIX(a*CH4+a*(nO/nf)*O2=[2,4,6,7,8]);

e) Plantear el sistema de ecuaciones que permiten determinar la composición, el poder calorífico y la temperatura de equilibrio adiabática en el proceso último, indicando las incógnitas y los datos.

Empiezo suponiendo xCH4=0 y quitando la última ecuación (luego lo comprobaré).

La Tad será la que haga nulo el calor que sale (Qs=0). Representando los resultados en función de la T:

>

n:=7:arr:=array(1..n,1..7):for i from 1 to n do T:=evalf(2000+2000*(i/n))*K_;sol1_:=fsolve(subs(dat,{eqNX,eqBC,eqBH,eqBO,eq1,eq2}),{a,x[Comp[2]],x[Comp[4]],x[Comp[6]],x[Comp[7]],x[Comp[8]]},{a=0..1,x[Comp[2]]=0..1,x[Comp[4]]=0..1,x[Comp[6]]=0..1,x[Comp[7]]=0..1,x[Comp[8]]=0..1});PCI_:=PCI(subs(sol1_,eqM/a));eqBE_:=q[s]/a=subs(cpComp_,sol1_,dat,PCI_-sum(delta[ii]*x[Comp[ii]]*c[p,Comp[ii]],ii=1..C_)*(T-T25)/a);Qs_:=subs(sol1_,rhs(eqBE_)/a);arr[i,1]:=T/K_;arr[i,2]:=subs(SI0,Qs_)/1e6;arr[i,3]:=subs(sol1_,x[Comp[2]]);arr[i,4]:=subs(sol1_,x[Comp[4]]);arr[i,5]:=subs(sol1_,x[Comp[6]]);arr[i,6]:=subs(sol1_,x[Comp[7]]);arr[i,7]:=subs(sol1_,x[Comp[8]]);od: pl2:=pla(arr,2,1):pl3:=pla(arr,3,1):pl4:=pla(arr,4,1):pl5:=pla(arr,5,1):pl6:=pla(arr,6,1):pl7:=pla(arr,7,1):plot([pl2,pl3,pl4,pl5,pl6,pl7],T_K=0..4000,color=black);

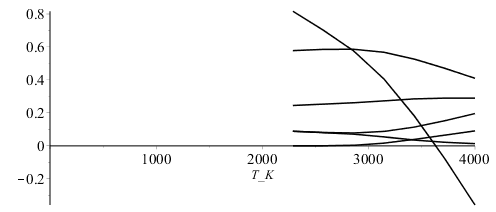i.e. la Tad es aprox. 3630 K. Comprobemos:

>

T:=3630*K_;sol1_:=fsolve(subs(dat,{eqNX,eqBC,eqBH,eqBO,eq1,eq2}),{a,x[Comp[2]],x[Comp[4]],x[Comp[6]],x[Comp[7]],x[Comp[8]]},{a=0..1,x[Comp[2]]=0..1,x[Comp[4]]=0..1,x[Comp[6]]=0..1,x[Comp[7]]=0..1,x[Comp[8]]=0..1});PCI_:=PCI(subs(sol1_,eqM/a));eqBE_:=q[s]/a=subs(cpComp_,sol1_,dat,PCI_-sum(delta[ii]*x[Comp[ii]]*c[p,Comp[ii]],ii=1..C_)*(T-T25)/a);Qs_:=subs(sol1_,rhs(eqBE_)/a);xCH4:=subs(sol1_,solve(eq3,x[CH4]));

Efectivamente, para 3630 K Qs=0 y xCH4=0.

>