>	restart:#"m16_p06"

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):

En una atmósfera inerte a 100 kPa y 25 °C, se tiene inicialmente una burbuja de jabón de 1 cm de radio llena de una mezcla combustible de metano y aire en proporción estequiométrica. En un cierto instante se provoca la reacción con una chispa central. Se pide:

a) Esquema de la configuración en tres instantes del proceso (inicial, intermedio y final), indicando la nomenclatura que se va a usar para la geometría y las variables

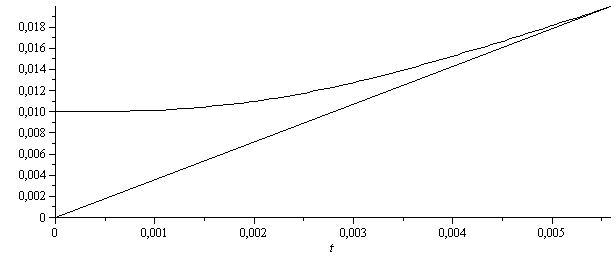
b) Explicar por qué es de esperar que el radio de la llama varíe linealmente con el tiempo, y hacer un esquema conjunto de la variación del radio de la llama y del radio de la burbuja en función del tiempo, deduciendo una expresión analítica para esta

c) Calcular la temperatura de la llama suponiendo combustión

d) Calcular el radio

e) Calcular la velocidad observable de la llama y el tiempo que tarda en arder la burbuja, suponiendo que la velocidad de deflagración es de 0,45

Datos:

>	su1:="Aire":su2:="H2O":dat:=[Mf_=0.016*kg_/mol_,R0=0.01*m_,V[q]=0.45*m_/s_];

Eqs. const.:

>	Adat:=get_gas_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):dat:=op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:

a) Esquema de la configuración en tres instantes del proceso (inicial, intermedio y final), indicando la nomenclatura que se va a usar para la geometría y las variables

b) Explicar por qué es de esperar que el radio de la llama varíe linealmente con el tiempo, y hacer un esquema conjunto de la variación del radio de la llama y del radio de la burbuja en función del tiempo, deduciendo una expresión analítica para esta

c) Calcular la temperatura de la llama suponiendo combustión

d) Calcular el radio

>	eqM:=eqMIX(a*CH4+b*(c21*O2+c79*N2)=[3,4,5]);sol1_:=solve(subs(dat,{eqNX,eqBC,eqBH,eqBO,eqBN}),{a,b,x[Comp[3]],x[Comp[4]],x[Comp[5]]});A_:=subs(sol1_,b/a);PCI_:=PCI(subs(sol1_,eqM/a));Ta_:=subs(cpComp_,sol1_,dat,T25+a*PCI_/sum(delta[i]*x[Comp[i]]*c[p,Comp[i]],i=1..C_));

>

eqBM1:=n=p0*(4/3)*Pi*r[F1]^3/(R[u]*T[F1]);eqBM:=n=(p0*(4/3)*Pi/R[u])*(r[B]^3/T[B]+(r[F]^3-r[B]^3)/T[F]);eqBM2:=n=p0*(4/3)*Pi*r[B2]^3/(R[u]*T[B2]);eqBM_1:=dr[F]/dt=(r[B]^2/r[F]^2)*(1-r[F1]^3/r[B2]^3)*dr[B]/dt;eqBM_2:=r[F1]^3/r[B2]^3=T[F1]/T[B1];eqBM_2_:=subs(T[F1]=T0,T[B1]=Ta_,dat,eqBM_2);eq1_:=r[F1]=subs(dat,R0);eq2_:=r[B2]=evalf(subs(eq1_,solve(eqBM_2_,r[B2])[1]));

e) Calcular la velocidad observable de la llama y el tiempo que tarda en arder la burbuja, suponiendo que la velocidad de deflagración es de 0,45

>	eqKIN:=dr[B]/dt=V[q]*Ta/T0;eqKIN_:=subs(Ta=Ta_,dat,eqKIN):evalf(%,2);eq3:=t[q]=r[B2]/(dr[B]/dt);eq3_:=t[q]=subs(solve({eqKIN_,eq2_,eq3},{t[q],dr[B],r[B2]}),t[q]);

>	rB:=subs(SI0,rhs(eqKIN_))*t:'rR'=evalf(%,2);rF:=subs(dat,((R0/m_)^3+rB^3*(1-T0/Ta_))^(1/3)):'rF'=evalf(%,2);plot({rB,rF},t=0..subs(eq3_,t[q])/s_,color=black);

>