| > | restart:#"m15_p79" |
En los datos de un motor de automóvil diésel, figura una potencia de 51 kW, un consumo, 3,9 L cada 100 km, y unas emisiones de CO2 de 108 g/km y 0,3 g/km de NOx. Aproximando las propiedades del diésel por las del dodecano, y el NOx por NO, se pide:
a) Calcular las emisiones de CO2 correspondientes a dicho consumo de fuel.
b) Rendimiento motor que correspondería al consumo y la potencia dados, suponiendo una velocidad de 90 km/h.
c) Para disminuir las emisiones de NOx en los motores modernos suele inyectarse una pequeña cantidad de urea (CO(NH2)2) en disolución acuosa. Si el proceso se aproxima por una etapa de generación de amoniaco, CH4N2O+H2O=2NH3+CO2, seguida de la de reducción, 4NO+4NH3+O2=4N2+6H2O, ¿cuánta urea sería necesaria para eliminar 0.3 g de NO por km?
d) Calcular las entalpías y entropías de reacción estándar de ambas reacciones, interpretando el signo obtenido.
Datos:
| > | read`../therm_chem.m`:with(therm_chem):with(therm_proc): |
| > | su1:="C12H26";su2:="CO2":su3:="NO":su4:="CH4N2O":su5:="NH3":su6:="O2":su7:="H2O":dat:=[Wdot=51e3*W_,V_L=0.039e-6*m_^3/m_,v=(90/3.6)*m_/s_,E_CO2=108e-6*kg_/m_,E_NOx=0.3e-6*kg_/m_]; |
Eqs. const. (nótese que tomamos la densidad del dodecano, 780 kg/m3, pese a que la del diesel suele ser de unos 830 kg/m3):
| > | dat:=op(dat),op(subs(g=g0,[Const])),SI2,SI1:datF:=get_liq_data(su1):datCO2:=get_gas_data("CO2"):datNO:=get_gas_data("NO"):datNH3:=get_gas_data("NH3"):datN2:=get_gas_data("N2"):datO2:=get_gas_data("O2"):datW:=get_gas_data("H2O"):rho[F]=subs(datF,rho); |
a) Calcular las emisiones de CO2 correspondientes a dicho consumo de fuel.
Usamos el modelo de combustión completa (el NOx lo trataremos aparte).
El CO2 producido es independiente de los gases inertes y del exceso de oxígeno, así que usamos simplemente la relación de estequiometría.
| > | eqC:=eq_fit(C12H26+a*O2=b*CO2+c*H2O);eqMf:=Mf(C12H24);eqF:=mf_L=rhof*V_L;eqF_:=subs(rhof=rho,datF,dat,%);eqF__:=lhs(%)=rhs(%)*(1e3*m_/km_)*(1e3*g_/kg_);eqCO2:=mCO2_L=rhof*V_L*(12*MCO2/Mf);eqCO2_:=subs(rhof=rho,Mf=rhs(eqMf),datF,MCO2=M,datCO2,dat,%);eqCO2__:=lhs(%)=rhs(%)*(1e3*m_/km_)*(1e3*g_/kg_); |
| (1) |
i.e. si consumiera solo 3,9 L cada 100 km de diésel (30 g/km), emitiría 96 g/km de CO2.
En realidad consumirá más combustible (el valor que se publica es el consumo mínimo) y emitirá más CO2. Por el efecto de la mayor densidad del diésel respecto al dodecano, el incremento sería solo del 6,4 % (830/780=1,064). El consumo de fuel a los 100 km aumenta al aumentar la velocidad; los valores usuales publicados son el consumo en circuito urbano (con velocidad media de unos 20 km/h y punta de 50 km/h) y en carretera (con velocidad media de unos 65 km/h y punta de 120 km/h). La emisión de CO2 es proporcional al consumo, 9,6/3.9=2,5 kg de CO2 por cada litro de diésel, con este modelo (en la práctica suele ser de 2,6 kg/L).
b) Rendimiento motor que correspondería al consumo y la potencia dados, suponiendo una velocidad de 90 km/h.
| > | eqeta:=eta=Wdot/Qdot;eqeta:=eta=Wdot/(mfdot*PCI);PCI_:=PCI(eqC);PCI_:=PCI_/rhs(eqMf);eqFdot:=mfdot=mf_L*v;eqFdot_:=subs(eqF_,dat,%);eqFdot__:=lhs(%)=rhs(%)*1e3*g_/kg_;eqeta_:=subs(eqFdot_,PCI=PCI_,eqF_,dat,eqeta);"Error: W/Q>1"; |
| (2) |
Imposible; ha de ser eta=W/Q<1, y aunque se usara el PCS o la exergía del fuel todavía saldría eta=1,4. La explicación es que esa potencia es la máxima (e.g. la que desarrollaría el coche a la velocidad máxima), mientras que ese consumo es a una volocidad moderada, e.g. a 50 km/h (el consumo a la velocidad máxima del coche, que es muy superior a la máxima permitida, sería más del doble. A unos 90 km/h (en llano, sin aire acondicionado, ni luces nocturnas), aunque el motor pudiera consumir solo esos 3,9 L a los 100 km, la potencia desarrollada podría ser tan solo de unos 10 kW y por tanto eta=1,50·10/51=0,30). El exceso de potencia de los motores es necesario para las aceleraciones, subidas, aire acondicionado, y demás accesorios.
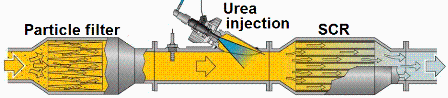
c) Para disminuir las emisiones de NOx en los motores modernos suele inyectarse una pequeña cantidad de urea (CO(NH2)2) en disolución acuosa. Si el proceso se aproxima por una etapa de generación de amoniaco, CH4N2O+H2O=2NH3+CO2, seguida de la de reducción, 4NO+4NH3+O2=4N2+6H2O, ¿cuánta urea sería necesaria para eliminar 0.3 g de NO por km?
| > | eqNO:=mNO_L=subs(dat,E_NOx);eqDesc:=CH4N2O+H2O=2*NH3+CO2;eqMurea:=Mf(su4);eqRed:=2*NO+2*NH3+(1/2)*O2=2*N2+3*H2O;eqU_NO_mol_:=2;eqU_NO_mass:=eqU_NO_mol*Murea/MNO;eqMNO:=M=subs(datNO,M);eqU_NO_mass_:=2;eqU:=mU_L=rhs(eqNO); |
| (3) |
i.e. la descomposición de 1 mol de urea genera 2 moles de NH3, que reducen otros 2 moles de NO, luego, 60 g de urea reducen 2·30=60 g de NO, y por tanto, para reducir los 0,3 g/km de NO que salen del motor, habría que añadir 0,3 g/km de urea (en disolución), i.e. 0,3 kg de urea cada 1000 km. La disolución suele ser del orden de 1 kg de urea por 2 kg de agua, así que con un depósito de 1 litro se tiene disolución para 1000 km.
La adición de urea acuosa para la reducción de NOx, catalítica (SRC o no (SNCR), ya se usa en grandes vehículos (autobuses, camiones).
d) Calcular las entalpías y entropías de reacción estándar de ambas reacciones, interpretando el signo obtenido.
| > | hgs_Desc:=hgs_r25(eqDesc);hgs_Red:=hgs_r25(eqRed); |
| (4) |
i.e. en condiciones estandar (25 ºC y 100 kPa), la descomposición de la urea es endotérmica (requiere añadir 133 kJ/mol) y aumenta la entropía (2 moles condensados dan lugar a 3 moles gaseosos); la reducción del NO es exotérmica (desprende 946 kJ/mol), y la entropía disminuye (4,5 moles de gas dan lugar a 2 moles de gas y 3 moles de líquido, a 25 ºC y 100 kPa).
En la práctica, las reacciones no tienen lugar a 25 ºC sino a alta temperatura (a la salida del motor), por lo que con el H2O(v), la eqDesc daría hr=89 kJ/mol (en vez de 13 kJ/mol), y la eqRed daría hr=-814 kJ/mol (en vez de 946 kJ/mol). Al enfriamiento que produce la hidrólisis de la urea hay que añadir el enfriamiento evaporativo debido a la inyección de la disolución atomizada.
| > | hr_v_Desc:=2*h37_+h4_-h52_-h6_;hr_v_Red:=2*h3_+3*h6_-2*h11_-2*h37_-h2_/2;; |
| (5) |

Autobús repostando a la vez combustible (diésel, manguera superior) y reductor (urea, manguera inferior).
| > |