>	restart:#"m15_p68"

>	read`../therm_chem.m`:with(therm_chem);with(therm_proc):

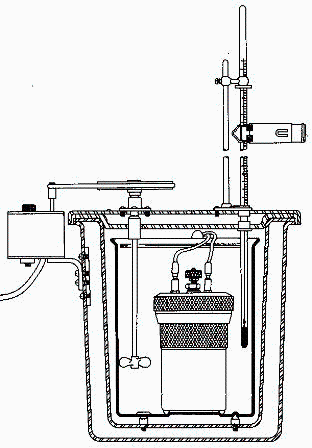
En una bomba calorimétrica de 0,3 L de capacidad se dispone una muestra de 0,6 g de naftaleno (C10H8), se tapa, y se inyecta lentamente oxígeno puro hasta una presión manométrica de 3 MPa, se produce la combustión, y se obserba que la temperatura del los 1,6 kg de agua del baño ha aumentado en 2,34 K. Sabiendo que el ambiente está a 25 ºC y 100 kPa, se pide:

a) Cantidad de nitrógeno atrapado, y cantidad de oxígeno total (el atrapado más el introducido).

b) Relación oxígeno/combustible y comparación con la estequiométrica.

c) Calcular el poder calorífico superior despreciando la entalpía de formación del combustible.

d) Temperatura adiabática de combustión.

e) Balance enrgético del calorímetro.

Datos:

>	su1:="O2":su2:="N2":su3:="H2O":fuel:=C10H8:dat:=[V=0.3e-3*m_^3,mf=0.6e-3*kg_,p1=3e6*Pa_,T1=(25+273.15)*K_,p0=0.1e6*Pa_,T0=(25+273.15)*K_,mB=1.6*kg_,DT=2.34*K_];

Eqs. const.:

>	dat:=op(dat),op(subs(g=g0,[Const])),SI2,SI1:Odat:=get_gas_data(su1):Ndat:=get_gas_data(su2):Wdat:=get_liq_data(su3):

a) Cantidad de nitrógeno atrapado, y cantidad de oxígeno total (el atrapado más el introducido).

>	nN:=c79*p0*V/(R[u]*T0);nN_:=subs(dat,nN);mN:=nN*MN;mN_:=subs(Ndat,nN_*M)*1e3*g_/kg_;nO:=p1*V/(R[u]*T1);nO_:=subs(dat,nO);mO_:=subs(Odat,nO_*M)*1e3*g_/kg_;

i.e. hay 0,0096 mol de N2 (0,27 g) y se introducen 0,36 mol de O2 (11,6 g).

b) Relación oxígeno/combustible y comparación con la estequiométrica.

>	nf:=mf/Mf;Mf:=evalf(((10*12+8*1)/1000))*kg_/mol_;nf_:=subs(dat,mf/Mf);Rox_f:='nO/nf';Rox_f_:=nO_/nf_;eqST:=fuel+12*O2=10*CO2+4*H2O;Rox_fstq:=12;Rox_f_Rox_fstq:=Rox_f_/Rox_fstq;

i.e.  había 4,7 mmol de fuel y 0,36 mol de O2, que es 77,5 molO/molF, mientras que la estequiométrica es 12 molO/molF (luego se metió 6,5 veces el estequiométrico).

c) Calcular el poder calorífico superior despreciando la entalpía de formación del combustible.

La diferencia por ser a V=cte será pequeña.

>	eqST_:=10*C+4*H2+12*O2=10*CO2+4*H2O;eq15_5;PCS_:=PCS(eqST_);PCSm_:=PCS_/Mf;DeltaPCS_Vp:=Dn_gas*R[u]*T25;Dn_gas:=10+4-12;DeltaPCS_Vp_:=subs(dat,DeltaPCS_Vp);

i.e. PCS=40 MJ/kg (5079 kJ/mol a p=cte y 5084 kJ/mol a V=cte).

d) Temperatura adiabática de combustión.

El valor estándar es el de p=cte, pero en este experimento se trata de V=cte

>

eq15_7_2;PCI_:=PCI(eqST_);eqMix_:=eqMIX(a*(10*C+4*H2+Rox_f_*O2)=[2,4,5]);sol1_:=fsolve({eqNX,eqBC,eqBH,eqBO,eqBN},{a,x[Comp[2]],x[Comp[3]],x[Comp[4]],x[Comp[5]]});eqTa_p:=subs(sol1_,cpComp,dat,eq15_7_3);eqTa_V:=subs(c[p,i]=c[V,i],eq15_7_2);eqTa_V:=Ta=subs(cpComp,sol1_,Const,dat,T25+a*PCI_/(sum(delta[i]*x[Comp[i]]*(c[p,Comp[i]]-R[u]),i=1..C_)));

i.e. a p=cte los gases llegarían a 1960 K, y a V=cte alcanzarían 2440 K (algo menos porque se disociaría parte del CO2 a CO y O2, y por la transmisión de calor a las paredes).

e) Balance enrgético del calorímetro.

>	eqBE:=mf*PCSm=(mB*cB+C)*DT;Q:=lhs(%);Q_:=subs(dat,mf*PCSm_);C_:=subs(Wdat,dat,mf*PCSm_/DT-mB*c);

i.e. se liberan 23,8 kJ de energía química, que pasan a calentar el agua del baño y el resto del calorímetro (cuerpo de la bomba y demás instrumentos), cuya capacidad térmica global es de unos 3500 J/K (que corresponderían a unos 7 kg de acero inoxidable de c=500 J/(kg·K)). Las bombas calorimétricas no suelen ser tan pesadas (la del laboratorio es de 2,5 kg).

>