>	restart:#"m15_p62"

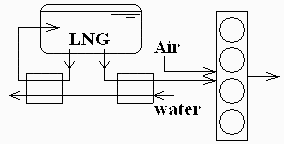
Para la propulsión de un cierto buque se usan 4 motores que generan 8 MW en total y consumen 150 L/s en total de gas natural a 20 ºC y 500 kPa (además de una pequeña cantidad de fuelóleo para la ignición de la mezcla combustible/aire). El gas se toma de un depósito de 220 m3 conteniendo gas natural licuado a 1 MPa. De pide:
a) Gasto másico de combustible y de aire necesario, suponiendo una relación aire/combustible relativa a la teórica de =2.
b) Rendimiento motor.

c) Composición de los gases de escape.
d) Autonomía de combustible.
e) Calor que hay que suministrar al gasto de LNG para los motores, y gasto másico de agua para conseguirlo con una entrada a 25 ºC y salida a 22 ºC.
f) Calor que hay que suministrar al tanque para mantener la presión durante el suministro (en realidad se calienta un pequeño flujo de LNG derivado del tanque), y la temperatura a la que saldría el agua de calefacción si se usa como entrada la salida descrita en el apartado anterior.

Datos:

>	read`../therm_chem.m`:with(therm_chem);with(therm_proc):

>	su0:="Aire":su1:="CH4":su2:="H2O":dat:=[Wdot=8e6*W_,VFdot=0.15*m_^3/s_,T2=(20+273.15)*K_,p2=500e3*Pa_,V=220*m_^3,p1=1e6*Pa_,Tw1=(25+273)*K_,Tw2=(22+273)*K_,lambda=2];

Eqs. const.:

>	Adat:=get_gas_data(su0):Gdat:=get_gas_data(su1),get_liq_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):dat:=op(dat),Const,SI2,SI1:get_pv_data(su1):

a) Gasto másico de combustible y de aire necesario, suponiendo una relación aire/combustible relativa a la teórica de =2.

Como nos dan el gasto volumétrico, basta multiplicar por la densidad en esas condiciones. Usamos el modelo de gas ideal.

>	mFdot:=p2*VFdot/(R*T2);mFdot_:=subs(Gdat,dat,%);eq15_3_;eqA0:=Ateo(su1);A_:=subs(dat,lambda*rhs(%));Am:=A*M[a]/M[f];Am_:=subs(A=A_,M[f]=Mf,M[a]=M,Adat,Mf=M,Gdat,%);mAdot:='Am*mFdot';mAdot_:=Am_*mFdot_;

i.e., el consumo de gas natural es de 0,49 kg/s, y el de aire17 kg/s.

b) Rendimiento motor.

Referido al PCI como es habitual, el rendimiento es:

>	eqeta:=eta='Wdot/(mFdot*PCI)';eq:=CH4+2*O2=CO2+2*H2O;PCI_:=PCI(%);PCIm_:=subs(Gdat,PCI_/M);eqeta:=eta=subs(dat,Wdot/(mFdot_*PCIm_));

i.e. el rendimiento energético es del 32%, un poco bajo para lo que es usual (entorno al 40%).

c) Composición de los gases de escape.

>	eqM:=eqMIX(a*CH4+a*A*(c21*O2+c79*N2)=[2,3,4,6]);sol1_:=subs(A=A_,dat,solve({eqBC,eqBH,eqBO,eqBN,eqNX},{a,x[CO2],x[O2],x[H2O],x[N2]}));

i.e. 75% de N2, 10% de H2O, 10% de O2 y 5% de CO2.

ADICIONAL

d) Autonomía de combustible.

1º calculamos la masa de CH4 a tanque lleno. Usaremos el modelo de líquido perfecto.

>	eqEB:='p1=pv(T1)';T1_:=evalf(subs(dat,solve(eqEB,T1)));'T1_'=TKC(T1_);m_max:=rho*V;rho=subs(Gdat,rho);m_max_:=subs(Gdat,dat,m_max);t_auto:='m_max/mFdot';t_auto_:=m_max_/mFdot_;'t_auto_'=%*h_/(3600*s_);

i.e., caben hasta 93 toneladas (aunque nunca se llena del todo por seguridad), lo que, con el consumo especificado, supone 52,5 horas de autonomía.  

NOTA. Se ha supuesto densidad constante (la del punto de ebullición normal a -161 ºC) aunque la densidad del líquido saturado a 1 MPa es realmente de 360 kg/m3 (disminuye desde 450 kg/m3 en el punto triple a 160 kg/m3 en el punto crítico).

e) Calor que hay que suministrar al gasto de LNG para los motores, y gasto másico de agua para conseguirlo con una entrada a 25 ºC y salida a 22 ºC.

Se toma líquido (LNG) a 1 MPa y 148 K y se quiere que entre al motor gaseoso a 0,5 MPa y 288 K, luego, despreciando las ganancias no intencionales, habrá que comunicarle un Qdot_vap=mdot*(h2-h1).

Con los modelos de líquido perfecto y gas perfecto:

>	Qdot_vap='mFdot*(h2-h1)';h2=hv(T);h1=hl(T);h2_:=subs(Gdat,T=T0,dat,hv(T));h1_:=subs(Gdat,T=T1_,dat,hl(T));Qdot_vap_:=subs(dat,mFdot_*(h2_-h1_));mw:='Qdot_vap/(c*(Tw1-Tw2))';mw_:=subs(Qdot_vap=Qdot_vap_,Wdat,dat,%);

i.e., hay que añadir 380 kW al LNG destinado a los motores (se haría en un cambiador de calor con agua de mar o mejor agua dulce de la refrigeración de los motores, para sinergia). El gasto de agua necesario sería de unos 30 kg/s a plena carga. Parece conveniente ajustar las presiones al final de la vaporización y no al principio.

f) Calor que hay que suministrar al tanque para mantener la presión durante el suministro (en realidad se calienta un pequeño flujo de LNG derivado del tanque), y la temperatura a la que saldría el agua de calefacción si se usa como entrada la salida descrita en el apartado anterior.

>	eqBE:=Qdot_pres='mFdot*hlv';hlv=hlv(T);h[lv0]=subs(Gdat,h[lv0]);hlv_:=subs(Gdat,T=T1_,dat,hlv(T));eqBE:=Qdot_pres=subs(Gdat,dat,mFdot_*hlv_);Tw3:=Tw2-Qdot_pres/('mw'*c);Tw3_:=subs(Qdot_vap=Qdot_vap_,eqBE,dat,%);'Tw3'=TKC(%);

i.e., hay que añadir otros 230 kW para que no caiga la presión en el tanque de LNG, saliendo el agua de calefacción a 20 ºC. (En realidad a 1 MPa hlv=415 kJ/kg en vez de los 510 kJ/kg del modelo de fluidos perfectos.)

NOTA. Puede verse el origen de los datos y otros detalles adicionales en la Revista de Ingeniería Naval de Marzo de 2004, p. 50.

>