| > | restart:#"m13_p79" |
Considérese una cáscara esférica de diámetro 0,2 m y 1 mm de espesor, de Al-6061 anodizado en negro, expuesta al sol en órbita LEO a 300 km en el punto subsolar. Se pide:
a) Determinar las cargas tĂ©rmicas externas y la temperatura estacionaria suponiendo que la conductividad fuese dominante. ÂżQuĂ© resultado se obtendrĂa despreciando el efecto de la Tierra?
b) Calcular la temperatura en el punto enfrentado con el sol (0º), y a 90º y 180º, en el caso de que la cáscara fuese de un material mal conductor y estuviese aislada radiativamente por el interior.
c) Considérese un modelo de dos nodos (hemisferios iluminado y posterior). Plantear las ecuaciones nodales en el régimen transitorio, y determinar los factores de vista involucrados.
d) Determinar las temperaturas nodales en régimen estacionario despreciando la conductividad térmica en los bordes.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):interface(warnlevel=0,displayprecision=2): |
| > | dat:=[D=0.2*m_,delta=1e-3*m_,E=1361*W_/m_^2,z=300e3*m_,Tp=288.15*K_,epsilon[p]=0.61,rho[p]=0.3,Tinf=2.7*K_,k=180*W_/(m_*K_),alpha=0.90,epsilon=0.85];dat:=op(dat),Const,SI2,SI1: |
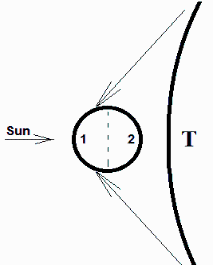
Se ha tomado para el Al-6061 anodizado en negro los datos de la Ref. 1, k=180 W/(m·K), alpha=0,90 y epsilon=0,85.
Nótese que la radiación a la semiesfera 1 también llega radiación emitida y reflejada por la Tierra, como se ha indicado en la figura.
a) Determinar las cargas tĂ©rmicas externas y la temperatura estacionaria suponiendo que la conductividad fuese dominante. ÂżQuĂ© resultado se obtendrĂa despreciando el efecto de la Tierra?
Supondremos radiaciĂłn solar puntual (colimada), con una irradiancia solar media E=1361 W/m2, y valores tĂpicos de albedo (30 %) y OLR:
| > | eqBE:=m*c*dT/dt=Qs+Qa+Qp-Qinf;Qs:=alpha*Af*E;Qa:=alpha*A*Fsp*rho[p]*E;Qp:=epsilon*A*Fsp*OLR;eqOLR:=OLR=epsilon[p]*sigma*Tp^4;Qinf:=epsilon*A*sigma*(T^4-Tinf^4);eqA:=A=Pi*D^2;eqA_:=evalf(subs(dat,%));eqFsp:=Fsp=(1-sqrt(1-1/h^2))/2;eqh:=h=(z+R[T])/R[T];eqh_:=subs(dat,%);eqFsp_:=subs(eqh_,dat,eqFsp); |
Como cuerpo negro:
| > | Qs_:=evalf(subs(alpha=1,Af=A/4,eqA_,dat,Qs));Qa_:=evalf(subs(alpha=1,eqFsp_,eqA_,eqh_,dat,Qa));eqOLR_:=evalf(subs(eqFsp_,eqA_,eqh_,dat,dat,eqOLR));Qp_:=evalf(subs(epsilon=1,eqOLR_,eqFsp_,eqA_,eqh_,dat,Qp));eqBE_:=subs(alpha=1,epsilon=1,dT=0,eqOLR_,Af=A/4,eqFsp_,eqA_,eqh_,dat,SI0,eqBE);T_:=solve(subs(alpha=1,epsilon=1,dT=0,eqOLR_,Af=A/4,eqFsp_,eqA_,eqh_,dat,SI0,eqBE))[1]*K_;'T_'=TKC(%);Tgeo_:=solve(subs(alpha=1,epsilon=1,dT=0,Af=A/4,eqA_,Fsp=0,dat,SI0,eqBE))[1]*K_;'Tgeo_'=TKC(%); |
i.e. del Sol se absorben 43 W directos, 18 W de albedo, y 11 W de IR planetario, resultando una TsteadyLEO=43 ÂşC que sin Tierra (e.g. en GEO) serĂa solo de 5 ÂşC.
Como cuerpo gris (es de esperar que quede más caliente porque alpha>epsilon):
| > | Qs_:=evalf(subs(Af=A/4,eqA_,dat,Qs));Qa_:=evalf(subs(eqFsp_,eqA_,eqh_,dat,Qa));eqOLR_:=evalf(subs(eqFsp_,eqA_,eqh_,dat,dat,eqOLR));Qp_:=evalf(subs(eqOLR_,eqFsp_,eqA_,eqh_,dat,Qp));eqBE_:=subs(dT=0,eqOLR_,Af=A/4,eqFsp_,eqA_,eqh_,dat,SI0,eqBE);T_:=solve(subs(dT=0,eqOLR_,Af=A/4,eqFsp_,eqA_,eqh_,dat,SI0,eqBE))[1]*K_;'T_'=TKC(%);Tgeo_:=solve(subs(dT=0,Af=A/4,eqA_,Fsp=0,dat,SI0,eqBE))[1]*K_;'Tgeo_'=TKC(%); |
i.e. del Sol se absorben 38 W directos, 16 W de albedo, y 9 W de IR planetario, resultando una TsteadyLEO=47 ÂşC que sin Tierra serĂa solo de 9 ÂşC.
b) Calcular la temperatura en el punto enfrentado con el sol (0º), y a 90º y 180º, en el caso de que la cáscara fuese de un material mal conductor y estuviese aislada radiativamente por el interior.
Si, además de k=0, se supone que la cáscara está aisladas por la cara interior (e.g. con MLI), habrĂa equilibrio local [W/m2] entre la absorciĂłn y la emisiĂłn. Los factores de vista desde parches planos respecto al planeta los tomamos de las Tablas de VF.
| > | eqBEstd:=q[abs]=q[emit];eqBE0:=alpha*E=epsilon*sigma*T0^4;T0bb_:=sqrt(sqrt(subs(dat,SI0,E/sigma)))*K_;T0_:=sqrt(sqrt(subs(dat,SI0,alpha*E/(epsilon*sigma))))*K_;eqBE90:=alpha*Ftp*rho[p]*E+epsilon*Ftp*OLR=epsilon*sigma*T90^4;eqFtp:=Ftp=(1/Pi)*(arctan(1/sqrt(h^2-1))-sqrt(h^2-1)/h^2);eqFtp_:=evalf(subs(eqh_,%));T90bb_:=sqrt(sqrt(subs(alpha=1,epsilon=1,eqFtp_,eqOLR_,dat,SI0,solve(eqBE90,T90^4))))*K_;T90_:=sqrt(sqrt(subs(eqFtp_,eqOLR_,dat,SI0,solve(eqBE90,T90^4))))*K_;eqBE180:=alpha*Fpp*rho[p]*E+epsilon*Fpp*OLR=epsilon*sigma*T180^4;eqFpp:=Fpp=1/h^2;eqFpp_:=subs(eqh_,%);T180bb_:=sqrt(sqrt(subs(alpha=1,epsilon=1,eqFpp_,eqOLR_,dat,SI0,solve(eqBE180,T180^4))))*K_;T180_:=sqrt(sqrt(subs(eqFpp_,eqOLR_,dat,SI0,solve(eqBE180,T180^4))))*K_; |
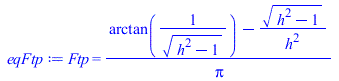 |
i.e. a 0Âş quedarĂa a 394 K si bb o a 399 K si real; a 90Âş quedarĂa a 245 K si bb o a 247 K si real; y a 180Âş quedarĂa a 319 K si bb o a 322 K si real.
Para todas las posiciones (modelo bb) serĂa asĂ:
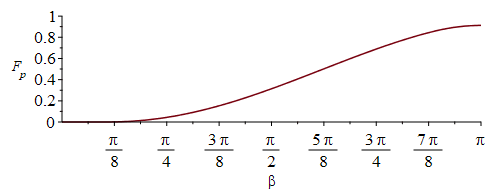
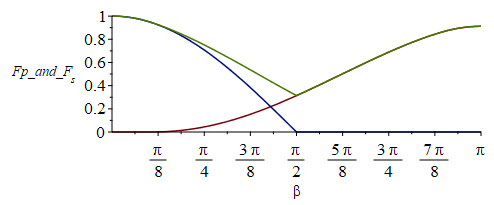
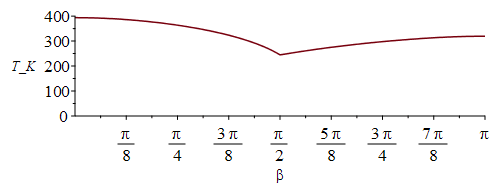
| > | F12_bsmaller:=cos(beta)/h^2:y:=-sqrt(h^2-1)*cot(beta):F12_bgreater:=-(sqrt(h^2-1)*sin(beta)*sqrt(1-y^2))/(Pi*h^2)+arctan(sin(beta)*sqrt(1-y^2)/sqrt(h^2-1))/Pi+cos(beta)*arccos(y)/(Pi*h^2):F12_b:=piecewise(beta<arccos(1/h),F12_bsmaller,F12_bgreater):F12_b_back:=piecewise(beta<arccos(1/h),0,subs(beta=Pi-beta,F12_bgreater)):i:='i':Fp:=piecewise(beta<Pi/2,F12_b_back,subs(beta=Pi-beta,F12_b)):plot(subs(eqh_,Fp),beta=0..Pi,F[p]=0..1);Fs:=piecewise(beta<Pi/2,cos(beta),0):plot([subs(eqh_,Fp),Fs,subs(eqh_,Fp)+Fs],beta=0..Pi,Fp_and_F[s]=0..1);eqBEb:=E*Fs+Fp*(rho[p]*E+OLR)=sigma*Tb^4:Tb_:=subs(eqh_,eqFpp_,eqOLR_,dat,SI0,sqrt(sqrt((E*Fs+Fp*(rho[p]*E+OLR))/sigma))):plot(Tb_,beta=0..Pi,T_K=0..400);plot([T_/K_-273,Tb_-273],beta=0..Pi,T_C=-30..120); |
 |
 |
 |
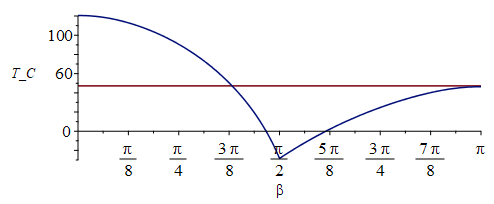 |
donde Fp es el factor de vista de un parche inclinado hacia la Tierra (empieza en beta=0,3 rad=17Âş), Fs=cos(b) es la proyecciĂłn solar, y T la temperatura de equilibrio radiativo. NĂłtese que beta=1.35 rad (77Âş) ya es mayor la carga planetaria que la solar (Fp>Fs), pero aun asĂ, el mĂnimo es para beta=90Âş. Se ha superpuesto la Tisotbb=43 ÂşC.
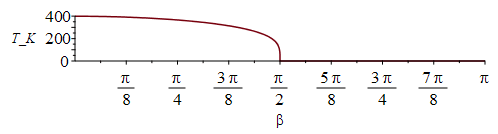
TambiĂ©n es interesante el caso de despreciar el efecto del planeta. Si solo queda el sol y el vacĂo, como la irradiancia normal a un parche de la esfera varĂa con cos(beta), pero la temperatura T=(E·cos(beta)/sigma)^(1/4) varĂa con cos(beta)^(1/4), resulta que a beta=60Âş donde solo se absorbe la mitad de lo de beta=0, la temperatura solo baja un 16 %, de 394 K a 331 K).
| > | Tb__:=(alpha*E*cos(beta)/(epsilon*sigma))^(1/4);plot(piecewise(beta<Pi/2,subs(dat,SI0,%),0),beta=0..Pi,T_K=0..400); |
 |
c) Considérese un modelo de dos nodos (hemisferio iluminado y posterior). Plantear las ecuaciones nodales en el régimen transitorio, y determinar los factores de vista involucrados.
Sea 1 la parte iluminada y 2 la opuesta, con subĂndices para las caras exterior 'e' e interior, 'i'. Como el recinto interior solo tiene 2 nodos, existe soluciĂłn explĂcita para el acoplamiento radiativo.
| > | eqBE1:=m1*c1*dT1/dt=Q1e+Q1i;eqBE2:=m2*c2*dT2/dt=Q2e+Q2i;eqQ1e:=Q1e=Q1es+Q1ea+Q1ep-Q1einf;eqQ1e:=Q1e=alpha*E*Ah/2+alpha*Ah*F1ep*rho[p]*E+epsilon*Ah*F1ep*OLR-epsilon*Ah*sigma*T1^4;eqQ2e:=Q2e=Q2ea+Q2ep-Q2einf;eqQ2e:=Q2e=alpha*Ah*F2ep*rho[p]*E+epsilon*Ah*F2ep*OLR-epsilon*Ah*sigma*T2^4;eqQ12:=A*sigms*(T1^4-T2^4)*Fee;Fee:=1/((1-epsilon[1])/epsilon[1]+1/F1i2i+(1-epsilon[2])/epsilon[2]);Fee_:=subs(epsilon[1]=epsilon,epsilon[2]=epsilon,Fee);eqQ2i:=Q2i=Ah*sigma*(T1^4-T2^4)*Fee_+k*Ac*(T1-T2)/L12;eqQ1i:=Q1i=-'Q2i';eqAhemisphere:=Ah=A/2;eqAh_:=subs(eqA_,%);eqAcontact:=Ac=Pi*D*delta;eqAc_:=evalf(subs(dat,%));eqL12:=L12=Pi*D/2; |
![`/`(1, `*`(`+`(`/`(`*`(`+`(1, `-`(epsilon[1]))), `*`(epsilon[1])), `/`(1, `*`(F1i2i)), `/`(`*`(`+`(1, `-`(epsilon[2]))), `*`(epsilon[2])))))](images/p79_60.gif) |
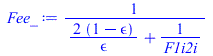 |
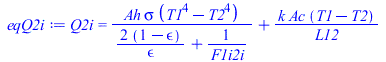 |
Factores de vista:
F12 interno (F1i2i). Sea 1 la parte iluminada, 2 la opuesta, y 3 una superficie plana virtual entre ellas (el cĂrculo máximo cuya circuferencia es la uniĂłn de las cascaras semiesfĂ©ricas). Es evidente que toda la radiaciĂłn que emitiera una cara de 3 llegarĂa Ăntegramente a su semiesfera correspondiente, i.e. F31=1, y por la reciprocidad de factores de vista, F13=A3·F31/A1=1/2, luego, eliminando la superficie auxiliar 3, vemos que la mitad de la radiaciĂłn emitida por 1 llegarĂa a 2 (la otra mitad sale de 1 y llega a 1, por ser cĂłncava).
F12 externos (F1ep y F2ep). El F2ep, desde una semiesfera convexa a un planeta viene en las TABLAS, asà como el de una esfera al planeta (Fsp), el cual será la media, Fsp=Ah·F1ep+Ah·F2ep)/A, por la propiedad distributiva, luego:
| > | eqF1i2i:=F1i2i=1/2;eqFsp:=Fsp=(F1ep+F2ep)/2;Fsp:=(1-sqrt(1-1/h^2))/2;F2ep:=(1-sqrt(1-1/h^2)+1/(2*h^2))/2;F1ep:=2*Fsp-F2ep;Fs:=subs(eqh_,[F1ep,F2ep,Fsp]) |
i.e. el casquete iluminado envĂa al planeta un 12 % de su radiaciĂłn externa, el casquete que apunta al nadir envĂa un 58 %, y la esfera en conjunto un 35 % como ya habĂamos visto.
d) Determinar las temperaturas nodales en régimen estacionario despreciando la conductividad térmica en los bordes.
Con k=0 el sistema es lineal en T^4. Como bb:
| > | eqBE1_:=subs(dT1=0,eqQ1e,eqQ1i,eqQ2i,k=0,eqh_,eqOLR_,eqAh_,eqAc_,eqL12,eqF1i2i,alpha=1,epsilon=1,dat,SI0,eqBE1);eqBE2_:=subs(dT2=0,eqQ2e,eqQ2i,eqQ1e,eqh_,eqOLR_,eqAh_,eqAc_,eqL12,eqF1i2i,alpha=1,epsilon=1,dat,SI0,eqBE2);sol_:=fsolve({eqBE1_,eqBE2_},{T1,T2},{T1=100..500,T2=100..500});T1_:=subs(sol_,T1)*K_;'T1_'=TKC(%);T2_:=subs(sol_,T2)*K_;'T2_'=TKC(%); |
i.e. con k=0 y bb, T1=59 ÂşC y T2=41 ÂşC (la media es 50 ÂşC, similar a los 43 ÂşC del modelo bb isotermo).
Con k=0 y grises:
| > | eqBE1_:=subs(dT1=0,eqQ1e,eqQ1i,eqQ2i,k=0,eqh_,eqOLR_,eqAh_,eqAc_,eqL12,eqF1i2i,dat,SI0,eqBE1);eqBE2_:=subs(dT2=0,eqQ2e,eqQ2i,eqQ1e,eqh_,eqOLR_,eqAh_,eqAc_,eqL12,eqF1i2i,dat,SI0,eqBE2);sol_:=fsolve({eqBE1_,eqBE2_},{T1,T2},{T1=100..500,T2=100..500});T1_:=subs(sol_,T1)*K_;'T1_'=TKC(%);T2_:=subs(sol_,T2)*K_;'T2_'=TKC(%); |
i.e. las temperaturas reales con k=0 son T1=64 ÂşC y T2=46 ÂşC. El factor de vista corregido Fee_ pasa de ser Fee_=F1i2i=1/2 a ser Fee_=0,43 con epsilon=0,85).
Con k=dado y cuerpo negro:
| > | eqBE1_:=subs(dT1=0,eqQ1e,eqQ1i,eqQ2i,eqh_,eqOLR_,eqAh_,eqAc_,eqL12,eqF1i2i,alpha=1,epsilon=1,dat,SI0,eqBE1);eqBE2_:=subs(dT2=0,eqQ2e,eqQ2i,eqQ1e,eqh_,eqOLR_,eqAh_,eqAc_,eqL12,eqF1i2i,dat,SI0,eqBE2);sol_:=fsolve({eqBE1_,eqBE2_},{T1,T2},{T1=100..500,T2=100..500});T1_:=subs(sol_,T1)*K_;'T1_'=TKC(%);T2_:=subs(sol_,T2)*K_;'T2_'=TKC(%); |
i.e. con conducción y bb baja de T1=59 ºC a T1=50 ºC y de T2=41 ºC a T2=35 ºC (la media es 42 ºC, ya prácticamente igual a los 43 ºC del modelo isotermo bb).
Con k=dado y cuerpo gris:
| > | eqBE1_:=subs(dT1=0,eqQ1e,eqQ1i,eqQ2i,eqh_,eqOLR_,eqAh_,eqAc_,eqL12,eqF1i2i,dat,SI0,eqBE1);eqBE2_:=subs(dT2=0,eqQ2e,eqQ2i,eqQ1e,eqh_,eqOLR_,eqAh_,eqAc_,eqL12,eqF1i2i,dat,SI0,eqBE2);sol_:=fsolve({eqBE1_,eqBE2_},{T1,T2},{T1=100..500,T2=100..500});T1_:=subs(sol_,T1)*K_;'T1_'=TKC(%);T2_:=subs(sol_,T2)*K_;'T2_'=TKC(%); |
i.e. se caliento un poco más como gris que como negro, como se esperaba..
| > |