| > | restart:#"m13_p78" |
ConsidĂ©rese una caja cĂşbica hueca de 0,2 m de arista y 1 mm de espesor, de Al-6061 anodizado en negro, en Ăłrbita geoestacionaria con el sol paralelo a la lĂnea que une vĂ©rtices opuestos del cubo, pudiĂ©ndose despreciar el efecto de otros cuerpos. Se pide:
a) Determinar la temperatura estacionaria suponiendo que la conductividad fuese dominante. Indicar el resultado que se obtendrĂa si la conductividad fuese despreciable.
b) Considérese un modelo de dos nodos. Plantear las ecuaciones nodales en el régimen transitorio.
c) Determinar los factores de vista involucrados (puede hacerse a partir del de dos caras opuestas).
d) Determinar las temperaturas nodales en régimen estacionario despreciando la conductividad térmica en los bordes.
e) Determinar las temperaturas nodales en régimen estacionario considerando la conductividad térmica en los bordes.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(plots): interface(displayprecision=2): |
| > | dat:=[L=0.2*m_,delta=0.001*m_,E=1361*W_/m_^2,k=180*W_/(m_*K_),Tinf=2.7*K_];dat:=op(dat),Const,SI2,SI1: |
a) Determinar la temperatura media estacionaria suponiendo que la conductividad fuese dominante. Indicar el resultado que se obtendrĂa si la conductividad fuese despreciable.
Recibe por las tres caras iluminadas, que forman con la dirección del sol y los vértices un ángulo alpha=arcsin(1/sqrt(3))=arctan(1/sqrt(2))=0,62 rad=35,3º, luego el área proyectada de una cara en la dirección del sol es A·cos(90º-alpha)=A·sin(alpha)=A/sqrt(3). El área total proyectada frontalmente es pues sqrt(3)·L^2, mientras que la emisión es por las 6 caras por igual al exterior (no hay flujos de calor por el interior al ser isotermo).
Supondremos radiaciĂłn solar puntual (colimada), con una irradiancia solar media E=1361 W/m2,y despreciaremos los efectos terrestres (la GEO está muy lejos, a 6,6 radios terrestres; lo máximo serĂa un albedo menor de los 10 W/m2 que recibirĂa una placa plana en el punto subsolar).
| > | eqEB0:=m*c*dT/dt=Wdis-Qrad;Wdis:=sqrt(3)*E*L^2;Qrad:=6*L^2*sigma*(T^4-Tinf^4);eqT:=T=(sqrt(3)*E/(6*sigma))^(1/4);evalf(subs(dat,%));eqEB0_:=evalf(subs(m=0,dat,SI0,eqEB0));T0_:=solve(%,T)[1]*K_;'T0_'=TKC(%); |
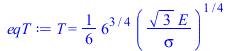 |
i.e. todas las caras del cubo quedarĂan a unos 15 ÂşC (unos 286 K).
Si la conductividad fuese despreciable. no habrĂa flujo de calor por conducciĂłn en llos bordes, y no valdrĂa el modelo de un solo nodo sino que aparecerĂan dos temperaturas bien diferenciadas: la de las tres caras iluminadas, y la de las tres caras traseras, y habrĂa un flujo de calor por radiaciĂłn entre ellas por el interior (se resuelve en el Ăşltimo apartado).
Si, además de k=0, se supone que las caras están aisladas por detrás (e.g. con MLI), cada cara iluminada recibirĂa radiaciĂłn solar proporcional a 1/sqrt(3), que habrĂa de compensarse con la radiaciĂłn propia hacia el espacio vacĂo, alcanzando una temperatura T=(E/(sqrt(3)*sigma))^(1/4)=70 ÂşC, mientras que las otras cinco caras no estarĂan expuestas mas que a la radiaciĂłn de fondo, por lo que alcanzarĂan Tinf=2.7 K. Este resultado es poco realista porque es muy difĂcil aislar tanto, y porque habrĂa que contar con la inflencia de la Tierra (IR y albedo).
b) Considérese un modelo de dos nodos. Plantear las ecuaciones nodales en el régimen transitorio.
| > | eqBE1:=m1*c1*dT1/dt=Wdis1-Qrad1e-Qrad12-Qcond12;eqBE2:=m2*c2*dT2/dt='Qrad12'+'Qcond12'- Qrad2e;Wdis1:=sqrt(3)*E*L^2;Qrad1e:=3*L^2*sigma*(T1^4-Tinf^4);Qrad12:=A1*F12*sigma*(T1^4-T2^4);Qcond12:=6*k*L*delta*(T1-T2)/L;Qrad2e:=3*L^2*sigma*(T2^4-Tinf^4); |
c) Determinar los factores de vista involucrados (puede hacerse a partir del de dos caras opuestas).
En la Tabla de factores de vista, entre placas iguales enfrentadas, se obtiene F12=0,2 entre caras opuestas, pero necesitamos el F12 entre los dos triedros opuestos., el cual puede deducirse a partir del anterior usando las propiedades de distribuciĂłn y de composiciĂłn, de la manera siguiente:
1º Como el factor de vista desde una cara a cualquiera de las otras cinco es 0,2, desde una cara iluminada al triedro no-iluminado será 3*0,2=0,6.
2º La composición del factor de vista del conjunto de las tres caras iluminadas (1,2,3) a las tres traseras (4,5,6), será:
| > | eqF:=F[`1+2+3`,`4+5+6`]=(A1*F[1,`4+5+6`]+A2*F[2,`4+5+6`]+A3*F[3,`4+5+6`])/(A1+A2+A3);eqF:=F12=3*0.6/3; |
i.e. el 60 % de lo que radia un triedro va hacia el otro (el otro 40 % va hacia sĂ mismo).
d) Determinar las temperaturas nodales en régimen estacionario despreciando la conductividad térmica en los bordes.
| > | eqBE1st_k0:=subs(m1=0,k=0,eqBE1);eqBE2st_k0:=subs(m2=0,k=0,eqBE2);eqBE1st_k0_:=subs(A1=L^2,F12=1,dat,SI0,eqBE1st_k0);eqBE2st_k0_:=subs(A1=L^2,F12=1,dat,SI0,eqBE2st_k0);sol_:=fsolve({eqBE1st_k0_,eqBE2st_k0_},{T1,T2},{T1=100..500,T2=100..500});T1_:=subs(sol_,T1)*K_;'T1_'=TKC(%);T2_:=subs(sol_,T2)*K_;'T2_'=TKC(%); |
i.e. con k=0 serĂa T1=51 ÂşC y T2=-44 ÂşC.
e) Determinar las temperaturas nodales en régimen estacionario considerando la conductividad térmica en los bordes.
| > | eqBE1st_k0:=subs(m1=0,eqBE1);eqBE2st_k0:=subs(m2=0,eqBE2);eqBE1st_k0_:=subs(A1=L^2,F12=1,dat,SI0,eqBE1st_k0);eqBE2st_k0_:=subs(A1=L^2,F12=1,dat,SI0,eqBE2st_k0);sol_:=fsolve({eqBE1st_k0_,eqBE2st_k0_},{T1,T2},{T1=100..500,T2=100..500});T1_:=subs(sol_,T1)*K_;'T1_'=TKC(%);T2_:=subs(sol_,T2)*K_;'T2_'=TKC(%); |
i.e. con la k del Al-6061, T1=29 ÂşC y T2=0 ÂşC. NĂłtese que estos valores son intermedios entre el caso de k=0 (T1=51 ÂşC y T2=-44 ÂşC), y el caso de k=infinito (T1=T2=15 ÂşC).
| > |